2018학년도 대학수학능력시험 6월 평가원 모의고사
수학이야기/수학능력시험 2017. 6. 4. 19:376월 평가원 모의고사 쉽지 않습니다. 올 수능이 비슷하게 나온다면 당황하는 수험생 많을 것으로 여겨집니다. 어렵다고 여겨지는 문제 풀이 올려둡니다.
21. 최고차항의 계수가 $1$인 사차함수 $f(x)$에 대하여 $$F(x)=\ln f(x)$$ 라 하고, 최고차항의 계수가 $1$인 삼차함수 $g(x)$에 대하여 $$G(x)=\ln g(x)\sin x$$ 라 하자. $$\lim_{x\rightarrow 1}(x-1)F^{\prime}(x)=3, \;\;\lim_{x\rightarrow 0}\frac{F^{\prime}(x)}{G^{\prime}(x)}=\frac{1}{4}$$ 일 때, $f(3)+g(3)$의 값은? [4점]
풀이) $$F(x)=\ln f(x)$$에서 $4$차 함수 $f(x)$는 미분가능하고 모든 실수에서 연속이다.
$$F^{\prime}(x)=\frac{f^{\prime}(x)}{f(x)}$$
$$\lim_{x\rightarrow 1}(x-1)F^{\prime}(x)=\lim_{x\rightarrow 1}\frac{(x-1)f^{\prime}(x)}{f(x)}=3$$
이므로 $f(1)=0$이다. $f(x)=(x-1)p(x)$ 라고 하여 다시 정리하면 (단, $p(x)$는 최고차항이 $1$인 $3$차함수)
$$\lim_{x\rightarrow 1}\frac{p(x) +(x-1)p^{\prime}(x) }{p(x)}=3$$
$$\lim_{x\rightarrow 1}\bigg(1+\frac{(x-1)p^{\prime}(x) }{p(x)}\bigg)=3$$
$$\lim_{x\rightarrow 1}\frac{(x-1)p^{\prime}(x) }{p(x)}=2$$
이므로 $p(1)=0$이다. 같은 방법으로 $p(x)=(x-1)q(x)$라고 생각하면
$$\lim_{x\rightarrow 1}\frac{(x-1)q^{\prime}(x) }{q(x)}=1$$
이므로 $q(1)=0$이다.
따라서 $f(x)=(x-1)^3(x-a)$의 꼴이다.
$$\frac{f^{\prime}(x)}{f(x)}=\frac{4x-3a-1}{(x-1)(x-a)}$$
$$G^{\prime}(x)=\frac{g^{\prime}(x)\sin x+g(x)\cos x}{g(x)\sin x}$$
$$\lim_{x\rightarrow 0}\frac{F^{\prime}(x)}{G^{\prime}(x)}=\lim_{x\rightarrow 0}\frac{g(x)\sin x}{g^{\prime}(x)\sin x+g(x)\cos x}\cdot \frac{4x-3a-1}{(x-1)(x-a)}$$
$$=\lim_{x\rightarrow 0}\frac{\sin x}{\frac{g^{\prime}(x)}{g(x)}\sin x+\cos x }\cdot \frac{4x-3a-1}{(x-1)(x-a)}$$
먼저 $g(0)=g^{\prime}(0)=0$이다. $\displaystyle{\lim_{x\rightarrow 0}\sin x=0}$이고 $g(x)$가 3차함수이므로 주어진 극한값이 존재하기 위해서는 반드시 분모에 $x$가 있어야 한다. 그러므로 $g(x)=x^3$이고 $a=0$이다.
$$\therefore f(x)=x(x-1)^3 ,\;\;g(x)=x^3$$
$$f(3)+g(3)=51$$
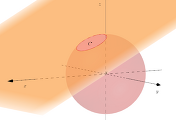
29. 좌표평면에서 중심이 $O$이고 반지름의 길이가 $1$인 원 위의 한 점을 $A$ , 중심이 $O$이고 반지름의 길이가 $3$인 원 위의 한 점을 $B$라 할 때, 점 $P$가 다음 조건을 만족시킨다.
(가) $\overrightarrow{OB}\cdot \overrightarrow{OP}=3\overrightarrow{OA}\cdot\overrightarrow{OP}$
(나) $|\overrightarrow{PA}|^2 +|\overrightarrow{PB}|^2 =20$
$\overrightarrow{PA}\cdot\overrightarrow{PB}$의 최솟값은 $m$이고 이때 $|\overrightarrow{OP}|=k$이다. $m+k^2$의 값을 구하시오. [4점]
풀이) 먼저 조건 가)를 살펴보자. $\overrightarrow{OB}\cdot \overrightarrow{OP}=3\overrightarrow{OA}\cdot\overrightarrow{OP}$에서
$$\overrightarrow{OB}\cdot \overrightarrow{OP}-3\overrightarrow{OA}\cdot\overrightarrow{OP}=0$$
$$(\overrightarrow{OB}-3\overrightarrow{OA})\cdot\overrightarrow{OP}=0$$
이다. 이때, 선분 $OA$의 연장선과 반지름이 $3$인 원이 만나는 점을 $A^{\prime}$이라고 하면
$\overrightarrow{A^{\prime}B}\cdot\overrightarrow{OP}=0$이므로 $\overrightarrow{A^{\prime}B}\bot\overrightarrow{OP}$이고 $\overline{OA^{\prime}}=\overline{OB}$이므로 점 $P$는 선분 $A^{\prime}B$의 수직이등분선 위에 있다.
조건 나)를 위치벡터로 나타내자.
$$|\overrightarrow{PO}+\overrightarrow{OA}|^2 +|\overrightarrow{PO}+\overrightarrow{OB}|^2 =20$$
$$2|\overrightarrow{PO}|^2+2\overrightarrow{PO}\cdot(\overrightarrow{OA}+\overrightarrow{OB})+|\overrightarrow{OA}|^2 + |\overrightarrow{OB}|^2 =20$$
$$|\overrightarrow{PO}|^2+\overrightarrow{PO}\cdot(\overrightarrow{OA}+\overrightarrow{OB})=5$$
이제 구하고자 하는 식을 위치벡터로 나타내자.
$$\overrightarrow{PA}\cdot\overrightarrow{PB}=(\overrightarrow{PO}+\overrightarrow{OA})\cdot(\overrightarrow{PO}+\overrightarrow{OB})$$
$$=|\overrightarrow{PO}|^2+\overrightarrow{PO}\cdot(\overrightarrow{OA}+\overrightarrow{OB})+\overrightarrow{OA}\cdot\overrightarrow{OB}=5+\overrightarrow{OA}\cdot\overrightarrow{OB}$$
$-3\leq\overrightarrow{OA}\cdot\overrightarrow{OB}\leq3$이므로
$\overrightarrow{PA}\cdot\overrightarrow{PB}$의 최솟값 $m=2$이다. 한편 $\overrightarrow{OA}\cdot\overrightarrow{OB}=-3$일 때는 두 벡터가 반대 방향일 때이다.
$(\overrightarrow{OA}+\overrightarrow{OB})//\overrightarrow{A^{\prime}B}$이므로
$$\overrightarrow{PO}\bot(\overrightarrow{OA}+\overrightarrow{OB})$$이다.
$$\overrightarrow{PO}\cdot(\overrightarrow{OA}+\overrightarrow{OB})=0$$이므로
가)에서 $k=\sqrt{5}$이다. 그러므로 $m+k^2=5$이다.
30. 실수 $a$와 함수 $f(x)=\ln(x^4 +1)-c$ ($c>0$인 상수)에 대하여 함수 $g(x)$를
$$g(x)=\int_{a}^{x}f(t)dt$$라 하자.
함수 $g(x)$의 그래프가 $x$축과 만나는 서로 다른 점의 개수가 $2$가 되도록 하는 모든 $a$의 값을 작은 수부터 크기순으로 나열하면 $\alpha_1, \alpha_2, \cdots , \alpha_m$ ($m$ 은 자연수)이다. $a=\alpha_1$일 때, 함수 $g(x)$와 상수 $k$는 다음 조건을 만족시킨다.
(가) 함수 $g(x)$는 $x=1$에서 극솟값을 갖는다.
(나) $\displaystyle{\int_{a}^{\alpha_m}g(x)dx=k\alpha_m\int_{0}^{1}|f(x)|dx}$
$mk\times e^c$의 값을 구하시오. [4점]
풀이) 주어진 조건에서 $g^{\prime}(x)=f(x)$이므로 도함수인 $f(x)$의 그래프를 통해서 함수 $g(x)$의 그래프를 추론할 수 있다.
$$f^{\prime}(x)=\frac{4x^3}{x^4 +1}$$이므로 함수 $f(x)$는 $x=0$에서 극솟값 $f(0)=-c$을 가진다.
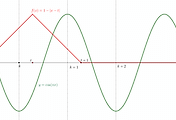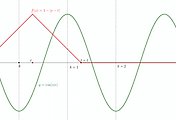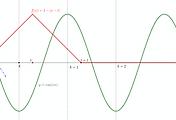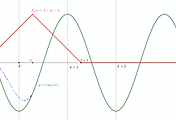
조건 가)에서 $g^{\prime}(1)=f(1)=0$이므로 $c=\ln 2$이다. 방정식 $f(x)=0$의 해는 $x=\pm 1$이고 $f(x)=f(-x)$이므로 $y$축 대칭이다. 따라서 함수 $f(x)$의 그래프는 아래와 같다.
$$\displaystyle{S=\int_{\alpha_1}^{\alpha_2}f(x)dx=\int_{\alpha_2=-1}^{\alpha_3 =1}|f(x)|dx=\int_{\alpha_3}^{\alpha_4}f(x)dx}$$
실수 $a$에 관계없이 함수 $g(a)=0$이므로 $g(x)=0$인 $x$의 값이 $2$개가 되도록 하는 $a$의 값은 위 그림과 같이 $4$개가 존재한다. $m=4$이다.
이제 함수 $g(x)$의 그래프를 추론해 보자.
| $x$ | $-1$ | $1$ | |||
| $g^{\prime}(x)=f(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $g(x)$ | $\nearrow$ | $g(-1)$ | $\searrow$ | $g(1)$ | $\nearrow$ |
함수 $g(x)$의 그래프는 아래와 같이 추론할 수 있다.
이 그래프는 함수 $f(x)$의 그래프가 $y$축에 대칭이므로 점 $H$에 대하여 대칭이다.
$\displaystyle{\int_{a}^{\alpha_m}g(x)dx}$는 그래프와 $x$축 사이에 있는 영역의 넓이이므로 직사각형 $OPQR$의 넓이와 같다.
$$\displaystyle{\int_{a}^{\alpha_m}g(x)dx=\alpha_m \times S=\alpha_m \int_{-1}^{1}|f(x)|dx=2\alpha_m \int_{0}^{1}|f(x)|dx}$$
이다. 따라서 $k=2$이다.
그러므로 $kme^c=2\times 4\times e^{\ln2}=16$이다.