벡터 외적(Cross product)

공간도형에서 평면 방정식은 법선벡터를 구해야 알 수 있다. 다르게 표현하면 평면 위에 있는 두 벡터에 동시에 수직인 벡터를 구해야 한다. 공간에 있는 세 점 $A(1,2,-1), B(-2,1,3), C(-1,0,1)$을 지나는 평면 방정식을 구해 보자.

법선벡터를 $\vec{n}=(a,b,c)$라고 하자. $\overrightarrow{AB}=(-3,-1,4),\;\;\overrightarrow{AC}=(-2,-2,2)$이고

$$\vec{n}\bot\overrightarrow{AB},\;\;\vec{n}\bot\overrightarrow{AC}$$

이므로 $$-3a-b+4c=0,\;\;-a-b+c=0$$

$2a-3c=0$에서 $\displaystyle{\frac{a}{3}=-\frac{c}{2}}$이므로 $a=5t,\;\;c=-t$이다. $b=-t$이므로 $\vec{n}=(3,-1,2)t$이다.

그러므로 평면 위의 점을 $X(x,y,z)$라고 하면 $\vec{n}\cdot\overrightarrow{AX}=0$에서

$$(3,-1,2)\cdot(x-1,y-2,z+1)=0$$

$$3x-y+2z+1=0$$

법선벡터를 구하는 과정을 공식으로 만들어 보자.

벡터 $\vec{n}=(x,y,z)$가 두 벡터 $\vec{a}=(a_1,a_2,a_3),\;\;\vec{b}=(b_1,b_2,b_3)$와 동시에 수직이라고 하자.

$$a_1x+a_2y+a_3z=0\;\;b_1x+b_2y+b_3z=0$$

$$x=(a_2 b_3-a_1 b_2)t,\;\;y=-(a_1 b_3-a_3 b_1)t,\;\;z=(a_1 b_2-a_2 b_1)t$$

임을 쉽게 확인할 수 있다. $(x,y,z)=(a_2 b_3-a_1 b_2, -a_1 b_3+a_3 b_1,a_1 b_2-a_2 b_1)$라고 할 수 있다. 이것을 외우기 쉽게 행렬식으로 정리하면 다음과 같다.

$$\Bigg(\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix},\;\;-\begin{vmatrix} a_1 & a_3 \\ b_1 & b_3\end{vmatrix},\;\;\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\Bigg)$$

고등학교 교육과정엔 없지만 과학고 심화수학 책에는 나오는 벡터 외적에 대해 정리해 둔다. 위에서 적은 벡터를 기본벡터를 써서 표현하면 아래와 같다.

$$\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix}\vec{e_1}-\begin{vmatrix} a_1 & a_3 \\ b_1 & b_3\end{vmatrix}\vec{e_2}+\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\vec{e_3}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}$$

참고 3차 행렬의 행렬식

가우스 소거법(Gaussian elimination)

이 벡터를 $\vec{a},\vec{b}$의 외적(cross product)이라 하고 기호로 $$\vec{a}\times\vec{b}$$로 쓴다. 두 벡터가 이루는 각을 $\theta$라고 하면 외적벡터 크기는

$$|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin\theta$$

이고 방향은 오른손 법칙을 따른다. 정리하면 두 벡터 $\vec{a},\vec{b}$에 수직인 단위벡터를 $\vec{n}$이라고 할 때,

$$\vec{a}\times\vec{b}=(|\vec{a}||\vec{b}|\sin\theta)\vec{n}$$

이다. 외적은 3차원 공간벡터에서만 정의되는 특별한 연산이다. 외적벡터는 두 벡터에 수직이고 두 벡터로 결정되는 평행사변형 넓이가 크기인 벡터이다.

외적의 성질

1) $\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$

2) $\big(k\vec{a}\big)\times\vec{b}=k\big(\vec{a}\times\vec{b}\big)=\vec{a}\times\big(k\vec{b}\big)$

3) $\vec{a}\times\big(\vec{b}+\vec{c}\big)=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}$

4)  $\big(\vec{a}+\vec{b}\big)\times\vec{a}=\vec{b}\times\vec{a}+\vec{c}\times\vec{a}$

기본벡터를 $\vec{i},\vec{j},\vec{k}$로 표현한다면 $$\vec{ i}\times \vec{i}=\vec{ j}\times \vec{j}=\vec{ k}\times \vec{k}=\vec{0}$$와 $$\vec{i}\times \vec{j}=-\vec{j}\times\vec{ i}=\vec{k},\;\;\; \vec{j}\times \vec{k}=-\vec{k}\times \vec{j}=\vec{i},\;\;\; \vec{k}\times \vec{i}=-\vec{i}\times \vec{k}=\vec{j}$$임을 활용하여 쉽게 계산할 수 있다.

한편 세 점을 꼭짓점으로 하는 삼각형 $ABC$의 넓이 $S$는

$$S=\frac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|$$와 같이 쉽게 구할 수 있다.

문제 세 점 $A(1,2,-1), B(-2,1,3), C(-1,0,1)$이 주어졌을 때  삼각형 $ABC$의 넓이를 구하여라.

학원에서 아주 흔하게 가르치는 이른바 사선공식도 쉽게 보일 수 있다.

세 점 $A(a_1,a_2,0), B(b_1,b_2,0), C(c_1,c_2,0)$를 꼭짓점으로 하는 삼각형의 넓이 $S$는

$$S=\frac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|=\frac{1}{2}| (b_1-a_1,b_2-a_2,0)\times(c_1-a_1,c_2-a_2,0) |$$

$$=\frac{1}{2}|(b_1-a_1)(c_2-a_2)-  (b_2-a_2)(c_1-a_1) |$$

$$=\frac{1}{2}|b_1a_2+c_1b_2+a_1c_2-(a_1b_2+b_1c_2+c_1a_2) |$$

외우기 쉽게 그림처럼 곱해서 차를 구한다고 가르친다. 그림을 보고 신발끈 공식으로 부르기도 한다. 모르는 이에게 신기해 보이는 공식이지만 알고 보면 별 것이 없다. 이런 걸 외우기 보다 차근차근 계산하는 것이 훨씬 좋다고 생각한다. 차라리 개념 정리를 하나 더 하는 것이 수학 공부에 도움이 될 것이다.

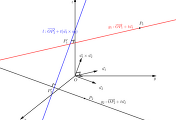
아래 그림에서 $\vec{a},\vec{b},\vec{c}$을 세 모서리로 하는 부피를 $V$라고 하자.

$$V=h |\vec{b} \times \vec{c}|=|\vec{a}| \cos \alpha | \vec{b} \times \vec{c} |= \vec{a}\cdot(\vec{b}\times \vec{c})$$