2018학년도 수시모집 카이스트 면접문제
수학이야기/면접논술 2018. 11. 6. 13:502017학년도부터는 선행학습 영향평가에서 모법답안을 공개하고 있으므로 카이스트 누리집을 보면 된다.
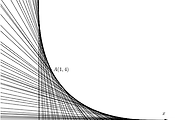
문제 1. 점$(r,0)$를 $P$라 하자. 중심이 점 $P$이고 반지름이 1인 원에 접하면서 $(0,0)$을 지나는 두 직선을 각각 $l_1 ,l_2$라 하자.
(1) (2점) 두 직선 $l_1 ,l_2$가 이루는 각을 $\theta$라 하자. $r=4$인 경우 $\sin\theta$의 값을 구하시오.
(2) (3점) 고정된 $r$에 대하여 점 $P=(r,0)$와 직선 $l_1$ 위의 점 $A$, 직선 $l_2$ 위의 점 $B$로 이루어진 삼각형 $ABP$의 둘레가 최소가 될 때 길이를 $a_r$이라 하자. 이때, $a_2 a_3 a_4\cdots a_8$의 값을 구하시오.
(1)
그림에서 $$\angle POA=\angle POB= \frac{\theta}{2}$$이다.
$P(4,0)$이라면 $\displaystyle{\sin\frac{\theta}{2}=\frac{1}{4}}$이므로 $\displaystyle{\cos\frac{\theta}{2}=\frac{\sqrt{15}}{4}}$이다.
따라서 $$\sin\theta=2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=\frac{\sqrt{15}}{8}$$이다.
(2) 그림에 점 $P$를 두 직선 $l_1,l_2$에 대칭이동한 점을 각각 $X,Y$라고 하자.
$\overline{AP}=\overline{AX},\;\;\overline{BP}=\overline{BY}$이므로 삼각형 $ABP$의 둘레의 길이는
$$\overline{AP}+\overline{AB}+\overline{BP}=\overline{AX}+\overline{AB}+\overline{BY}\geq\overline{XY}$$이므로 최솟값은 $\overline{XY}$이다.
점 $O$를 $(0,0)$이라 할 때, $\angle XOY=2\theta$이다. 삼각형 $XOY$는 $OX$와 $OY$의 길이가 $r$인 이등변삼각형이므로 $$\overline{XY}=2r\sin \theta$$
$P(r,0)$이라면 $\displaystyle{\sin\frac{\theta}{2}=\frac{1}{r}}$이고 $\displaystyle{\cos\frac{\theta}{2}=\frac{\sqrt{r^2 -1}}{r}}$이므로 $$\sin\theta=2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=2\frac{\sqrt{r^2 -1}}{r^2}$$이다.
따라서 $$a=4\frac{\sqrt{r^2 -1}}{r}=4\sqrt{\frac{r-1}{r}}\sqrt{\frac{r+1}{r}}$$이다.
$$a_2 a_3 a_4\cdots a_n = 4^{n-1}\sqrt{\frac{1\cdot 2\cdot 3\cdots (n-1)}{2\cdot 3 \cdot 4 \cdots n}}\sqrt{\frac{3\cdot 4\cdot 5\cdots (n+1)}{2\cdot 3 \cdot 4 \cdots n}}$$
$$=4^{n-1}\sqrt{\frac{1}{n}}\sqrt{\frac{n+1}{2}}=4^{n-1}\sqrt{\frac{n+1}{2n}}$$
$n=8$인 경우 답은 $$a_2 a_3 a_4\cdots a_8=4^7 \sqrt{\frac{9}{16}}=4^7 \times \frac{3}{4}=3\cdot 4^6 =12288$$
문제 2. 다항식 $F_1 (x), F_2 (x), F_3 (x), \cdots$가 아래 성질들을 만족한다.
$F_1 (x)=x-1$
$F_2 (x)=x^2 -1$
$F_{n+2}(x)=F_n (x)F_{n+1}(x)\;\;\;(n=1,2,3, \cdots )$
(1) (2점) $F_5^{\prime}(x)=0$이고 $-1<x<1$인 $x$를 구하시오.(2) (3점) $F_{99} (x)>0$을 만족하는 실수 $x$의 범위를 모두 구하시오.
풀이 $F_n (x)=(x-1)^{a_n}(x+1)^{b_n}$으로 쓸 수 있다.
이때, $a_1=1,a_2 =1, a_n =a_{n-1}+a_{n-2}$이며 $b_1=0,b_2 =1, b_n =b_{n-1}+b_{n-2}$인 점화식을 얻을 수 있다.
여기서 $a_n =b_{n+1}$임도 쉽게 알 수 있다.
점화식에 따라 구하면 $a_3 =2, a_4 =3, a_5=5$이다.
따라서 $ F_5 (x)=(x-1)^{5}(x+1)^{3}$이다.
$$F_5^{\prime}(x)=5(x-1)^4 (x+1)^3 +3(x-1)^5 (x+1)^2=(x-1)^4(x+1)^2(8x+2)$$
이 값이 0이 되려면 $\displaystyle{x=-\frac{1}{4}}$이다.
2) $F_{99} (x)=(x-1)^{a_{99}}(x+1)^{b_{99}}$이므로 $a_{99}$와 $b_{99}$가 홀수냐 짝수냐에 따라 $F_{99}$의 부호가 결정된다.
수열 $a_n$을 관찰하면 $1,1,2,3,5,8,\cdots$이므로 홀수, 홀수, 짝수로 주기 3으로 홀짝성이 되풀이 된다.
99는 3의 배수이므로 $a_{99}$는 짝수이고 $b_{99}$는 홀수이다.
따라서 $x\not=1$인 모든 실수에서 $(x-1)^{a_{99}}>0$이고 $x>-1$일 때, $(x+1)^{b_{99}}>0$이다.
따라서 $F_{99} (x)=(x-1)^{a_{99}}(x+1)^{b_{99}}>0$일 필요충분조건은 $x>-1,x\not=1$이다.
문제 3 실수 $a$에 대해 다음 두 부등식$$(y -e^x )(y-a) \leq 0,\;\;0 \leq x \leq 1$$
을 동시에 만족시키는 영역의 넓이를 $F(a)$라 하자.
(1) (2점) $F(0)$의 값을 구하시오.
(2) (3점) $F(a)$의 값이 최소가 되는 $a$를 구하시오.
풀이
1) $a=0$일 때, 부등식이 나타내는 영역은 정적분으로 넓이를 구할 수 있다.
$$\int_{0}^{1}e^x dx=e-1$$
2) $a \leq 1$일 때, $F(a)=\int_{0}^{1}(e^x-a)dx=e-1-a$이므로, $F(a) \geq F (1)$이다.
$a \geq e$일 때, $F(a)=\int_{0}^{1}(a-e^x)dx=a-e+1$이므로, $F(a) \geq F (e)$이다.
따라서, 최솟값은 $1\leq a \leq e$일 때, 생긴다.
(혹은 실제 계산을 통해서 나중에 나올 최솟값보다 더 크다고 할 수도 있다.)
(다른 풀이로는, 영역의 모양을 파악하고 나면, $a>e$인 경우 $a$를 줄이면 영역의 넓이가 줄어들므로 최소일 수 없다는 것을 알 수 있고, $a<1$인 경우 $a$를 증가시키면 영역의 넓이가 줄어들기 때문에 최소일 수 없다는 것을 알 수 있다.)
$1\leq a \leq e$인 부분에서 최소를 찾는 방법으로 세 가지 풀이가 있다.
하나, $x$축 따라 적분 계산하는 풀이:
$$F(a)=\int_{0}^{\ln a}(a-e^x)dx+=\int_{\ln a}^{1}(e^x -a)dx=a\ln a-(a-1)+(e-a)-(a-a\ln a)$$이다.
이제 $a$로 미분하면
$$F^{\prime}(a)=2\ln a-1$$
이므로 $\ln a=1/2$ 즉 $a=e^{1/2}$일 때 $F(a)$값이 최소가 됨을 알 수 있다.
답은 $a=\sqrt{a}$이다.
둘, $y$축 따라 적분 계산하는 풀이:
$y$축을 따라서 적분하여 넓이를 구하면
$$F(a)-\int_{1}^{a} \ln u du+\int_{a}^{1}(1-\ln u) du$$
이다. 미적분학의 기본정리를 쓰면
$$F^{\prime}(a)=\ln a-(1-\ln a)=2\ln a-1$$이다.
따라서, $\ln a=1/2$ 즉 $a=e^{1/2}$일 때 $F(a)$값이 최소가 됨을 알 수 있다.
셋, 직관적인 풀이:
$y=a$인 직선을 $y=a+\epsilon$으로 조금 움직였다고 할 때, $y=a$인 직선의 위쪽 부분이 부등식에 영역에 들어있는 길이에 비례하여 넓이가 줄어들고 $y=a$의 아래쪽 부분이 부등식에 영역에 들어있는 길이에 비례하여 넓이가 늘어난다. 따라서 $F(a)$값이 최소가 되려면 $F^{\prime}$이 0이어야 하므로 $y=a, \;\;0 \leq x \leq 1$인 선분이 정확하게 절반의 길이로 나뉘어서 절반은 해당 영역을 아래에서 만나고 절반은 해당 영역의 위에서 만나면 된다. $y=e^x$에서 절반 만나려면 $x=1/2$이면 되므로 이때 $a=y=e^{1/2}=\sqrt{e}$가 된다.
문제4. 다항함수 $f(x)=ax(x-1)(x-2)+x$에서 $a>0$인 실수이다.(1) (2점) 모든 $x$에 대하여 $f(x)$가 역함수를 가지는 $a$의 범위를 구하시오.
(2) (3점) 모든 $x$에 대하여 $f(x)$가 역함수를 $g(x)$를 가질 때, $x=1$에서 $f(x)$의 접선과 $g(x)$의 접선이 이루는 각이 $30^{o}$인 의 값을 구하시오.
풀이
(1)$f^{\prime}(x)=a(x(x-1)+x(x-2)+ (x-1)(x-2))+1$과 $f^{\prime\prime}(x)=a(6x-6)$이므로 $x=1$에서 $f^{\prime}(x)$가 최소값 $-a+1$를 갖는다. 따라서 $-a+1 \geq 0$이면 $f(x)$는 증가함수가 되고 역함수를 갖는다. 따라서 $f(x)$가 역함수를 가질 조건은 $0<a\leq1$이다. ($a$는 1이하라고 답을 해도 괜찮음)
다른 풀이: $f^{\prime}(x)=3ax^2 -6ax+(2a+1)$이고 $y=3ax^2 -6ax+(2a+1)$가 $x$축과 밑으로 내려가면 안된다. 따라서 $D=9a^2 -3a(2a+1)=3a(a-1)$이고 $0<a\leq1$를 얻을 수 있다.
(2) $x=1$에서 $f(x)=x$이므로 $f(x)$와 $g(x)$는 $(1,1)$에서 만난다. $f(x)$와 $g(x)$는 $y=x$에 대해서 대칭이므로 $(1,1)$에서 두 접선이 이루는 각이 $30°$인 경우에는, 접선과 $y=x$가 이루는 각이 $15°$가 된다.
따라서, 각각의 접선의 기울기가 $\tan(45°- 15°)$ 또는 $\tan(45°+ 15°)$가 되어야 한다. 따라서, $x=1$에서 $f^{\prime}(x)$가 $\tan(30°)$ 혹은 $\tan(60°)$이 되는 $a$의 값을 구해야한다.
$f^{\prime}(1)=-a+1$이고 $0<a\leq1$이므로 $-a+1=\tan(30°)=1/\sqrt{3}$이다.
따라서 $\displaystyle{a=1-\frac{1}{\sqrt{3}}}$이 된다.
(혹은, $a>0$인 경우, 아래 그림처럼 되므로, $f^{\prime}(1)=\tan(45°- 15°)=\tan(30°)=\displaystyle{\frac{1}{\sqrt{3}}}$가 선택되어야 하고, 따라서 $f^{\prime}(1)=-a+1$이고 $0<a\leq1$이므로 $-a+1=\tan(30°)=1/\sqrt{3}$이다.)