중3 제곱근과 무리수
수학이야기/중학수학3 2021. 4. 6. 22:02중학교 수학은 교과서를 얼핏 보고 가르치기 쉬울 것 같았는데 막상 시작해 보니 쉽지 않다. 무엇보다 학생들이 난생처음 만나는 어떤 개념을 설명하는 것이 쉽지 않다. 제곱근만 하더라도 고등학생에겐 설명할 필요가 없는 개념이다. 여러 가지 설명을 시도했으나 수학이 서툰 학생들은 여전히 어려워한다. 이 글은 쉽게 따라오지 못하는 학생을 위해 쓰는데 정작 실력이 부족한 학생도 쉽게 이해할 수 있을까 걱정스럽다. 방정식을 풀면서 수를 발견하는 과정으로 다가가 보기로 한다.
수학엔 등식이 있다.
$$2+3=5,\quad 7\times 9=63,\quad 8^2=64$$
이런 식은 그냥 계산식이라 하자. 왼쪽에서 오른쪽으로 하는 계산은 자연스럽다. 하지만 왼쪽에서 오른쪽으로 나아가는 일은 조금 생각을 해야 한다.
$$2+x=5,\quad x\times 9=63,\quad x^2 =64$$
이처럼 어떤 정해지지 않은 문자의 값을 구하는 식을 방정식이라 부른다. 여전히 크게 어렵지 않게 미지수 $x$를 구할 수 있다. 어렵지 않다는 뜻은 초등학생도 구할 수 있다는 말이다.
$$x+5=1$$
여전히 간단한 방정식이지만 초등학생을 풀 수 없다. 왜냐하면 음수를 모르기 때문이다. 중학교 1학년은 되어야 풀 수 있다. 수학을 배운다는 것은 우리가 풀 수 있는 방정식의 범위를 넓혀가는 것과 같다. 다르게 말하면 수의 범위를 넓혀가는 것이 수학 공부다.
중학교 3학년에서 새로운 수를 만난다.
방정식 $x^2=64$은 해결할 수 있다. 다시 말하면 거듭제곱해서 64가 되는 수는 쉽게 찾을 수 있다. 구구단을 열심히 외웠다면 또 음수를 제곱하면 양수가 된다는 사실을 잊지 않았다면 말이다.
답은 $x=-8$과 $x=8$이다. 이 두 수를 $64$의 제곱근이라고 한다. $8$은 쉽게 찾고 $-8$은 찾지 못한다면 갈 길이 멀다. 1학년에서 배운 음수를 다시 공부하자.
- 정의
- $a\geq0$에 대하여 $x^2=a$를 만족하는 $x$를 $a$의 제곱근이라고 하자.
양수의 제곱근은 양수와 음수 2개이며, 그 절댓값은 서로 같다. 0의 제곱근은 0이다. 거듭제곱해서 음수가 되는 수는 없으므로 생각하지 않는다.
교과서는 이 부분에서 바로 근호($\sqrt{\quad}$)를 도입한다.
양수 $a$의 제곱근 중에서 양수인 것을 양의 제곱근, 음수인 것을 음의 제곱근이라 하고, 기호 $\sqrt{\quad}$를 써서 다음과 같이 나타낸다.
이때 기호 $\sqrt{\quad}$를 근호라 하며, $\sqrt a$를 '루트(root) $a$'라고 읽는다. 또 둘을 한꺼번에 '$\pm \sqrt a$'로 쓰기도 한다.
$a$의 양의 제곱근은 $\sqrt a$, $a$의 음의 제곱근 $-\sqrt a$
이때 먼저 제곱수가 아닌 수의 제곱근이 존재하는 것을 먼저 생각하게 하고 근호를 말하는 것이 좋겠다.
$$x^2=1,\quad x^2=4,\quad x^2 =9$$
위에 있는 방정식과 아래에 있는 방정식은 수준이 다르다고 봐야 할 것이다.
$$x^2 =2$$
피타고라스 정리에 따라 한 변의 길이가 1인 대각선의 길이를 $x$라고 하면 $x$는 위에 있는 방정식을 만족한다.

제곱해서 2가 되는 수는 유리수가 아니다. 초등학생에겐 음수는 존재하지 않는 것처럼 중학교 3학년이 지나지 않은 학생에겐 이런 수는 없다. 하지만 피타고라스 정리를 쓰면 수직선 위에 반드시 있어야 하는 수임을 보일 수 있다. 이 새로운 수를 나타내기 위해 새로운 기호가 있어야 한다. 근호는 그래서 만든 것이다.
제곱해서 2가 되는 양수는 $\sqrt{2}$, 제곱해서 2가 되는 음수는 $-\sqrt{2}$로 쓴다.
뒷부분은 영상으로 정리한다. 계획 없이 만들어서 부족하지만 글로 쓰는 것보다 영상이 더 만들기 쉽다.
근호가 있는 식을 계산하는 법
곱셈과 나눗셈
$\sqrt 2 \times \sqrt 3$은 아래와 같이 계산한다.
$$\sqrt2 \times \sqrt 3 =\sqrt {2\times3} $$
왜일까? 좌변과 우변이 다른 점을 말해보자. 좌변은 제곱근 2와 제곱근 3을 곱한 것이다. 우변은 2와 3을 곱한 6의 양의 제곱근이다. 다시 말하면 제곱근을 먼저 구하고 곱셈을 한 것은 곱셈을 먼저하고 제곱근을 구한 것과 같음을 보여야 한다.
무리수도 수이므로 유리수와 마찬가지로 곱셈에서 교환법칙과 결합법칙이 그대로 성립해야 한다. 먼저 두 수 $\sqrt2$와 $\sqrt3$은 모두 양수이므로 두 수의 곱은 양수이다. 아래와 같이 두 수의 곱 $\sqrt 2 \times \sqrt 3$을 제곱하면 6이 된다.
$$\begin{split} (\sqrt2 \times \sqrt 3 )^2 &=( \sqrt2 \times \sqrt 3 )\times ( \sqrt2 \times \sqrt 3 )\\&= \sqrt2 \times \sqrt 3 \times \sqrt2 \times \sqrt 3 \\&=(\sqrt2\times\sqrt2)\times(\sqrt 3\times\sqrt 3) \\&=\sqrt{2}^2\times \sqrt{3}^2 \\&=6\end{split}$$
$\sqrt 2 \times \sqrt 3$은 제곱해서 6이 되는 양수이므로 $\sqrt{6}$이다.
나눗셈은 역수를 곱하는 것이니 다를 바가 없다.
두 실수 $a>0,\;\;b>0$에 대하여
$$\sqrt{a}\sqrt{b}=\sqrt{ab},\quad \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$$
제곱근의 뜻에 따라 $a>0$일 때, $\sqrt{a^2}=a$이다. 이 성질을 써서 조금 더 간결하게 표현할 수 있다.
$$\sqrt 2 \times \sqrt{6}=\sqrt{12}=\sqrt{2^2 \times 3}=2\sqrt3$$
위에 있는 계산은 사실 아래처럼 생각해야 더 쉽다.
$$\sqrt 2 \times \sqrt{6}=\sqrt{2}\times\sqrt 2 \times \sqrt 3=\sqrt{2}^2 \times \sqrt{3}=2\sqrt3$$
덧셈과 뺄셈
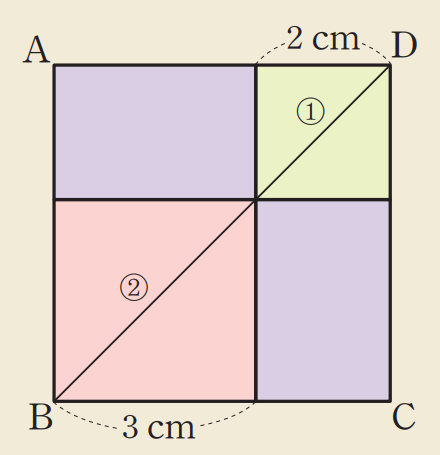
아래 그림에서 자연스럽게 근호 안에 있는 수가 같을 때를 유추할 수 있다.
$$2\sqrt 2 + 3\sqrt 2= 5\sqrt 2$$
기억하자. $\sqrt 2 +\sqrt3 \not= \sqrt{2+3}$이다. 곱셈공식을 안다면 쉽게 확인할 수 있다.
$$(\sqrt{2}+\sqrt{3})^2 =2+3+2\sqrt 6=5+2\sqrt6$$
칠교놀이는 아래와 같이 정사각형을 조각 7개로 나누고 다시 배치하여 여러 가지 모양을 만드는 전통 놀이이다. 한 변이 12인 정사각형을 잘라 만든 조각으로 만든 고양이 모양 도형은 둘레의 길이가 얼마일까?










