2018학년도_수학 가형 21번 풀이

21. 양수 $t$에 대하여 구간 $[1,\infty)$에서 정의된 함수 $f(x)$가

$$f(x) = \begin{cases} \ln x & \quad (1 \leq x < e)\\ -t+\ln x & \quad (x \geq e) \end{cases}$$

일 때, 다음 조건을 만족시키는 일차함수 $g(x)$ 중에서 직선 $y=g(x)$의 기울기의 최솟값을 $h(t)$라 하자.

$1$ 이상의 모든 실수 $x$에 대하여 $(x-e)\{g(x)-f(x)\}\geq 0$이다.

미분가능한 함수 $h(t)$에 대하여 양수 $a$가 $\displaystyle{h(a)=\frac{1}{e+2}}$을 만족시킨다. $\displaystyle{h^{\prime}\bigg(\frac{1}{2e}\bigg)\times h^{\prime}(a)}$의 값을 구하여라.[4점]

 

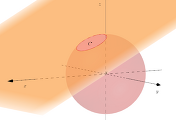
풀이 함수를 표현할 때 흔하게 쓰는 $y=f(x)$에 참 많은 것이 들어 있다. 함수를 파악하는 것은 변수를 파악하는 것이다. 먼저 함수 $f$를 표현한 식에서 $t$는 변수가 아니라 상수다. $x \geq e$인 부분을 $y$축 방향으로 $-t$만큼 평행이동하는 것이다. 움직이는 그림으로 나타내 보았다.

함수 $h(t)$로 나타나 있으므로 상수이던 $t$가 변수가 되는 것이다. 다시 말하면 조건을 만족하는 직선의 기울기 최솟값은 $t$에 따라 결정되는 함수값이다. 조건을 살펴보자.

 $(x-e)\{g(x)-f(x)\}\geq 0$이므로 

$x-e \leq 0$이면 $g(x)-f(x)\leq 0$이고 $x-e \geq0$이면 $g(x)-f(x)\geq$이다.

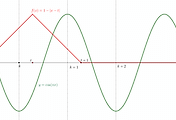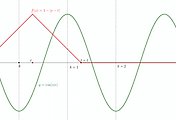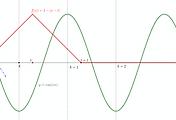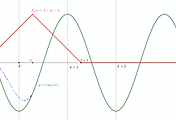
$1\leq x<e$일 때는 직선이 곡선보다 아래에 있고 $e\leq x$일 때는 직선이 곡선보다 위에 있다.

아래 그림과 같이 직선 $y=g(x)$는 평행이동하여 벌어진 틈새를 통과해야 하는데 이것은 파란 부분에서 접선이 점 $(1,0)$을 지날 때가 기울기가 최솟값임을 먼저 생각할 수 있다. 하지만 조금 더 관찰하면 그림과 같이 $t$값이 어떤 값보다 작다면 접선이 검은 부분을 자르게 됨을 알게 된다. 따라서 이 때는 두 점 $(1,0)$과 $(e,-t+1)$을 지나는 직선의 기울기가 최솟값이다.

$$h(t)=\frac{-t+1}{e-1}$$ 

 

 

경계는 어디가 될까? 점 $(e,-t+1)$이 접점이 될 때가 경계다. $\displaystyle{f^{\prime}(e)=\frac{1}{e}}$이므로 

$$h(t)=\frac{-t+1}{e-1}=\frac{1}{e}=f^{\prime}(e)$$

$$\therefore t= \frac{1}{e}$$

정리하면

$$h(t)=\frac{-t+1}{e-1}\;\;\bigg(0<t<\frac{1}{e}\bigg)$$ 

$$\therefore\;\;h^{\prime}\bigg(\frac{1}{2e}\bigg)=-\frac{1}{e-1}\tag{1}$$

$\displaystyle{\frac{1}{e} \leq t}$일 때는 간단하게 표현하기 어렵다.

접점 $B(x_1, -t+\ln x_1)$에서 접선의 방정식은 아래와 같다.

$$y-(-t+\ln x_1)=\frac{1}{x_1}(x-x_1)\;\;\because f^{\prime}(x_1)=\frac{1}{x_1}$$

이 직선이 점 $(1,0)$을 지나므로

$$t-\ln x_1=\frac{1}{x_1}(1-x_1)$$이다. 여기서 $\displaystyle{h(t)=\frac{1}{x_1}}$이므로 다시 정리하면

$$t+\ln h(t) =h(t)-1$$이다.

$\displaystyle{h(a)=\frac{1}{e+2}<\frac{1}{e}}$이므로

$$a>\frac{1}{e}$$

이다. 음함수의 미분법으로 양변을 $t$에 대하여 미분하자.

$$1+\frac{h^{\prime}(t)}{h(t)}=h^{\prime}(t)$$이다. $t=a$를 대입하자.

$$1+\frac{h^{\prime}(a)}{h(a)}=h^{\prime}(a)$$

$$\therefore\;\;h^{\prime}(a)= -\frac{1}{e+1}\tag{2}$$

마지막으로 (1) (2)에 의하여 

$$h^{\prime}\bigg(\frac{1}{2e}\bigg)\times h^{\prime}(a)=\frac{1}{(e-1)(e+1)}$$