과제 연습문제 풀이
17. A function continuous at only one point Let
$$f(n)=\begin{cases}x, & \mbox{if }x \mbox{ is a rational } \\0, & \mbox{if }x\mbox{ is irrational}\end{cases}$$
a. Show that $ƒ$ is continuous at $x = 0.$
b. Use the fact that every nonempty open interval of real numbers contains both rational and irrational numbers to show that ƒ is not continuous at any nonzero value of $x$.


18. The Dirichlet ruler function If $x$ is a rational number, then $x$ can be written in a unique way as a quotient of integers $m/n$ where $n>0$ and $m$ and $n$ have no common factors greater than $1$. (We say that such a fraction is in lowest terms. For example, $6/4$ written in lowest terms is $3/2$.)
Let $ƒ(x)$ be defined for all $x$ in the interval $(0,1)$ by
$$f(n)=\begin{cases}1/n, & \mbox{if }x = m/n\mbox{ is a rational number in lowest terms} \\0, & \mbox{if }x\mbox{ is irrational}\end{cases}$$
For instance, $ƒ(1/2) = 1/2, ƒ(1/3) = ƒ(2/3) = 1/3, ƒ(1/4) = ƒ(3/4) = 1/4$, and so on.
a. Show that $ƒ$ is discontinuous at every rational number in $(0,1)$.
b. Show that $ƒ$ is continuous at every irrational number in $(0,1)$. (Hint: If $P$ is a given positive number, show that there are only finitely many rational numbers $r$ in $[0,1]$ such that $ƒ(r) \geq \epsilon$.)
c. Sketch the graph of $ƒ$. Why do you think $ƒ$ is called the “ruler function”?
풀이 함수의 그래프는 아래와 같다.
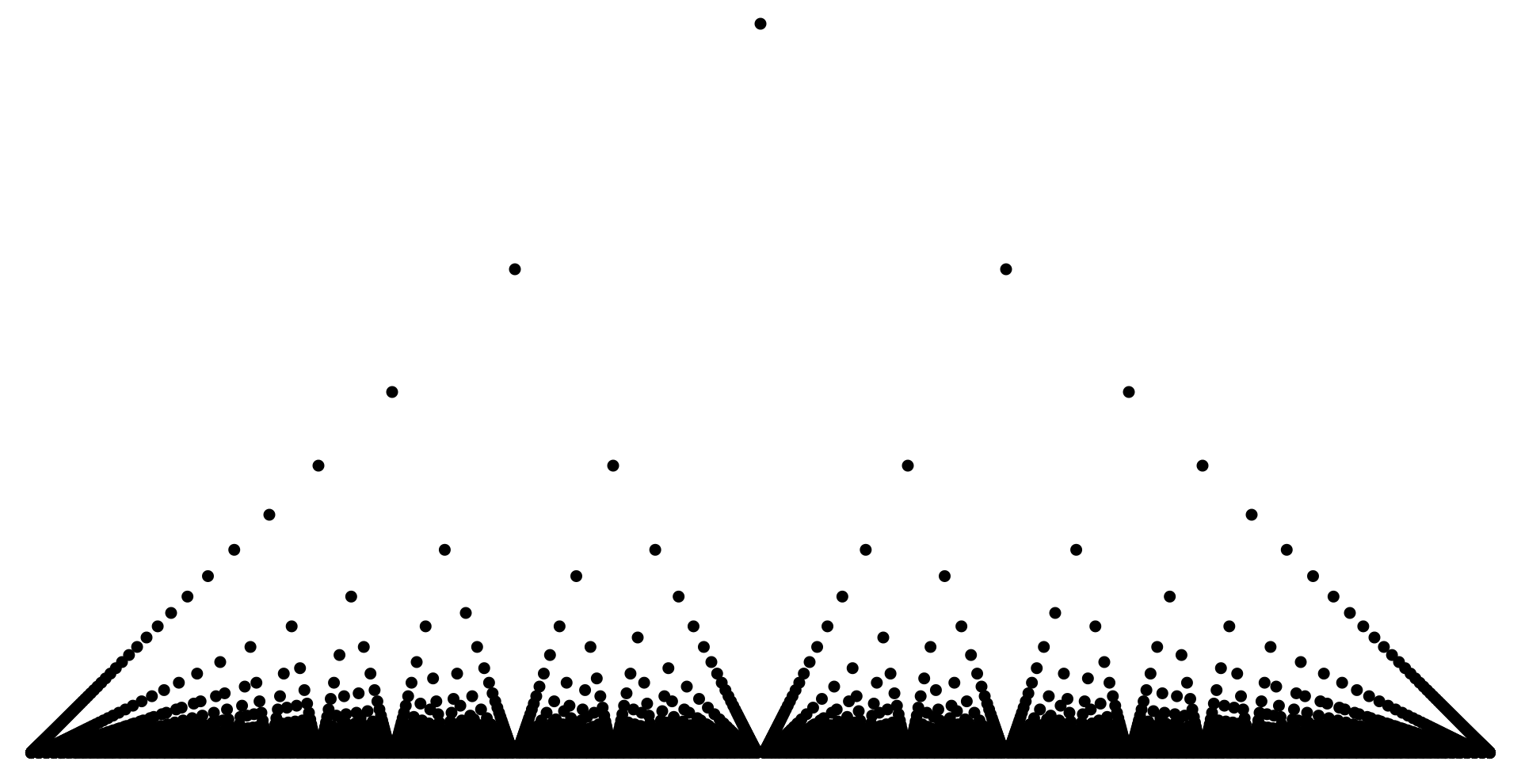
a. $f$는 닫힌 구간 $(0,1)$에 있는 모든 유리수에서 불연속임을 보이자.
$x_r$가 $f(x_0)=1/n$인 유리수라고 하고 $\epsilon=1/2n$이라고 하자.
$\delta>0$에 상관없이 열린 구간 $(x_r -\delta, x_r+\delta)$에는 반드시 무리수가 존재한다.
그 무리수를 $x$라고 하면 $$|f(x)-f(x_r)|=\bigg|0-\frac{1}{n} \bigg|= \frac{1}{n}>\frac{1}{2n}=\epsilon$$
이다.
따라서 $f$는 모든 유리수 $x_r$에서 불연속이다.
b. 먼저 주어진 $\epsilon>0$에 대하여 $f(r)>\epsilon$인 유리수는 구간 $(0,1)$에 유한개임을 보이자.
자연수 $N$에 대하여 $f(r)=1/N$인 유리수는 몇 개가 있을까?
$r=m/N$에서 $gcd(m,N)=1$인 자연수 $m$을 세는 것과 같다.
따라서 $N$이 소수(prime)라면 $N-1$개이고 합성수라면 $N-1$개보다 작다. 참고 오일러 $\phi$ 함수
$f(r)>1/N$인 유리수는 유한하므로 $f(r)\leq 1/N$인 유리수는 무한하다.
$\epsilon>0$이 주어진다면 무리수 $x_i$에 대하여 모든 $x\in(x_i-\delta, x_i+\delta)$에 대하여
$$f(x)\leq \frac{1}{N_{\epsilon}}<\epsilon$$
이 되도록 $\delta>0$와 자연수 $N_{\epsilon}$을 잡을 수 있다.
$x$가 무리수이면 $|f(x)-f(x_i)|=0<\epsilon$이고,
$x$가 유리수이면 $|f(x)-f(x_i)|=1/N_{\epsilon}<\epsilon$이다.
그러므로 $f$는 모든 무리수 $x_i$에서 연속이다.
c. 아래와 같이 그리면 자에 새겨진 눈금처럼 보인다.
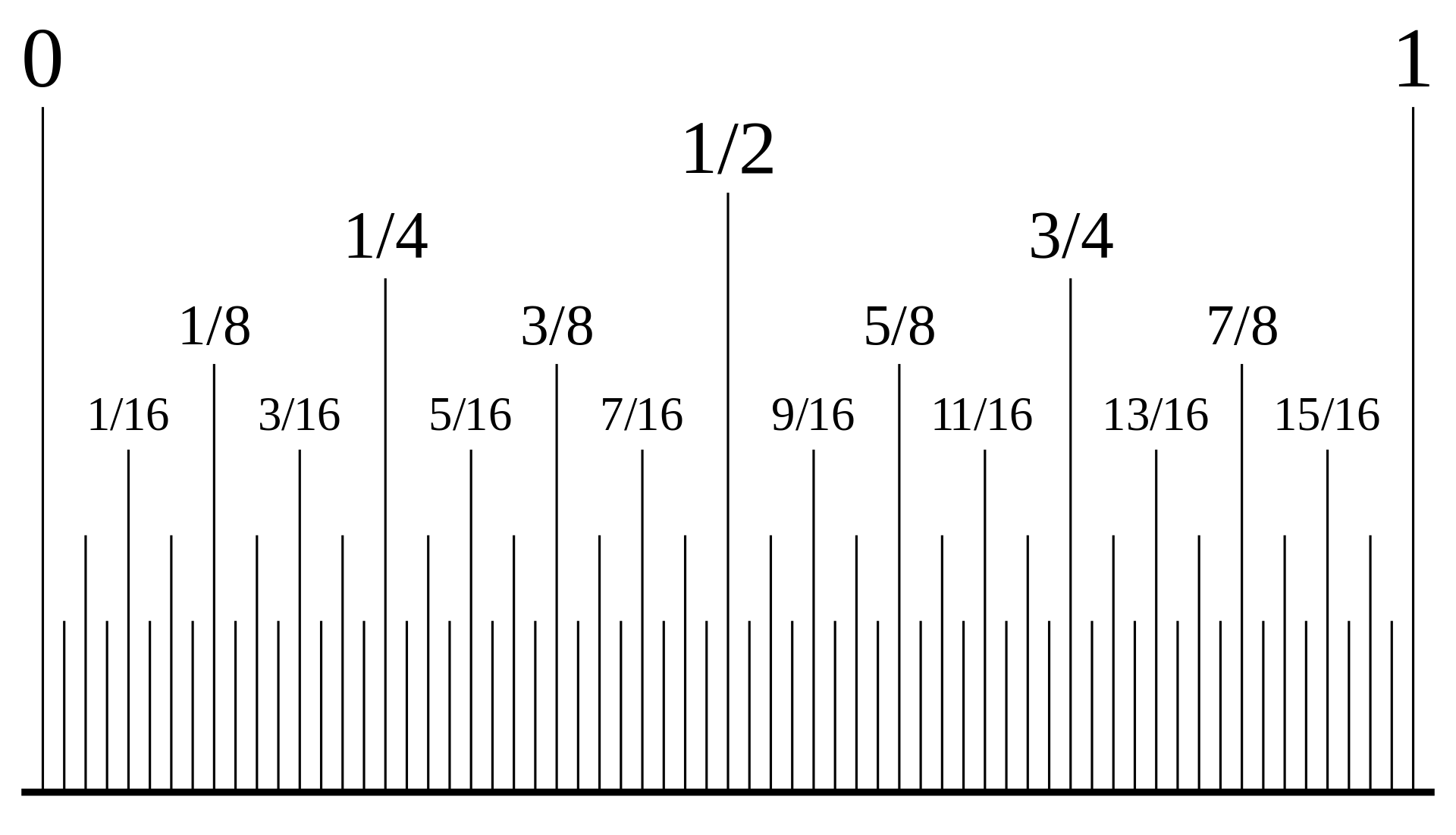
https://en.wikipedia.org/wiki/Thomae%27s_function
Thomae's function - Wikipedia
Point plot on the interval (0,1). The topmost point in the middle shows f(1/2) = 1/2 Thomae's function, named after Carl Johannes Thomae, has many names: the popcorn function, the raindrop function, the countable cloud function, the modified Dirichlet func
en.wikipedia.org