굴절 법칙 Snell's law
스넬 법칙은 굴절refractive을 정리한 법칙이다. 이 법칙을 끌어내는 다양한 방법이 있는데 여기서는 페르마 원리Fermat's principle에서 끌어내려고 한다. 위키백과에 있는 글에서 미분과 관련된 부분을 우리말로 옮기며 몇 가지 설명을 덧붙인다.
페르마의 원리: 빛은 항상 가장 이동 시간이 가장 짧은 경로를 따라 이동한다.
굴절률refractive index $n=c/v$은 주어진 매질에서 빛의 속도 $v$에 반비례 한다.($c$은 진공 상태에서 빛의 속도) 해변을 달리는 것이 바닷물에서 수영하는 것보다는 빠르다. 따라서 해변은 굴절률이 낮고 바닷물은 굴절률이 높다고 비유할 수 있다. 물에 빠진 사람을 구조하러 갈 때 가장 빠른 경로를 찾는 일을 생각해 보자. 아래 그림에서 매질 1은 해변, 매질 2는 바다로 생각하면 쉽게 이해할 수 있다.
빛이 매질medium 1에 있는 점 $Q$를 출발하여 굴절refractive되어 매질 2에 있는 점 $P$에 도착한다고 하자. 매질 1과 2에서 굴절률refractive index을 각각 $n_1$ and $n_2$이라고 하자. 빛은 경계에 있는 점 $O$를 지나 매질 2로 들어간다고 하자.
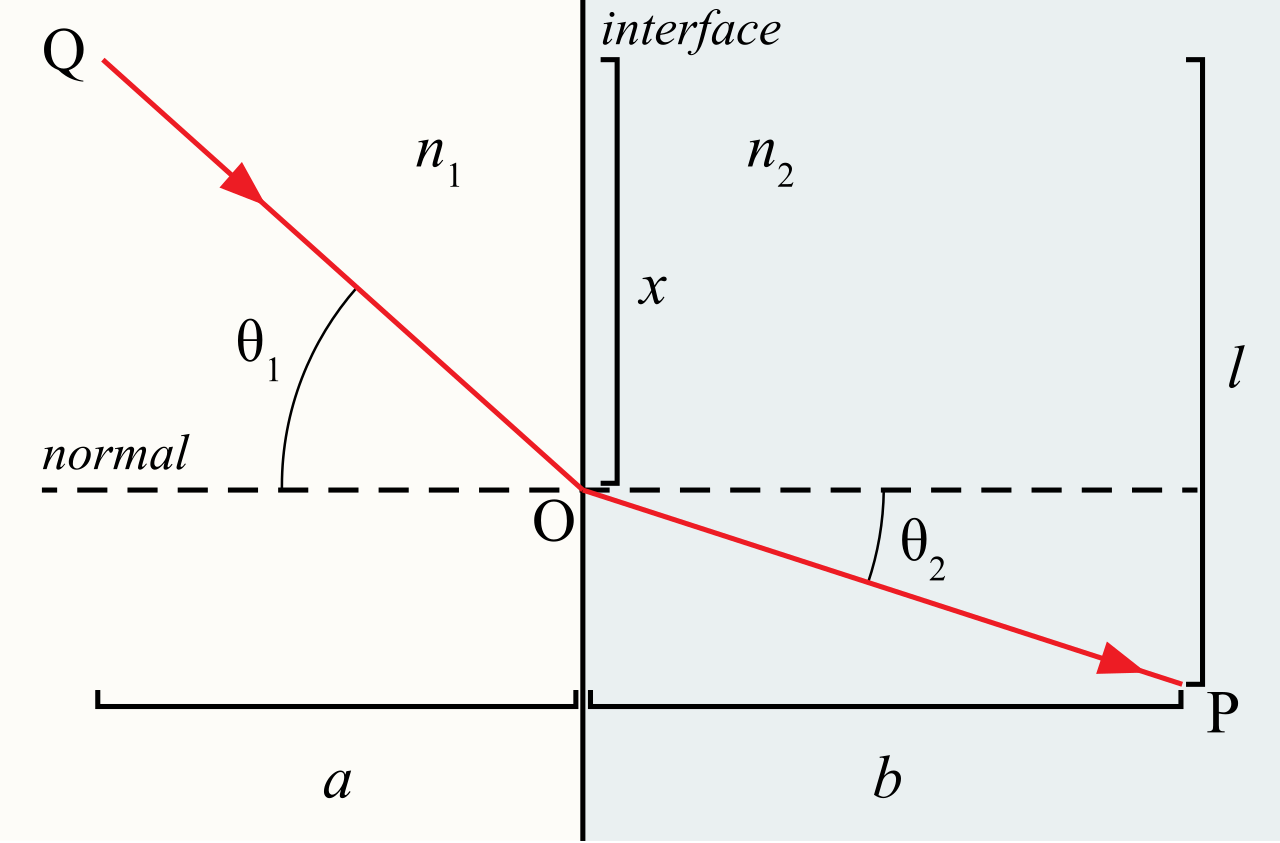
그림에서 법선normal에 대한 $\theta_1$은 입사각, $\theta_2$는 굴절각이고 매질 1과 2에서 광속을 각각 $v_1=c/n_1$과 $v_2=c/n_2$이라 하자.($c$은 진공 상태에서 빛의 속도, $\theta_1>0$)
빛이 점 $Q$를 출발하여 $O$를 지나 $P$에 도착할 때까지 걸리는 시간 $T$는 아래와 같이 나타낼 수 있다. 상수 $a, b, l$와 변수 $x$가 나타내는 것은 위 그림을 참고하자.
$$T=\frac{\sqrt{x^2 + a^2}}{v_1} + \frac{\sqrt{b^2 + (l - x)^2}}{v_2} \tag{1}$$
이제 페르마 원리에 따라 빛은 $T$가 최솟값을 가지는 경로를 따라 이동한다.
이제 $O$를 찾으면 된다.
(1)을 $x$에 대하여 미분하여 미분계수가 $0$인 점을 찾아보자.
$$\frac{dT}{dx}=\frac{x}{v_1\sqrt{x^2 + a^2}} + \frac{ -(l - x)}{v_2\sqrt{(l-x)^2 + b^2}}=0\tag{2}$$
함수 $\displaystyle{\frac{dT}{dx}}$는 구간 $[0,l]$에서 연속이고 $x=0,\;\;x=l$일 때, 함숫값은 각각 $\displaystyle{\frac{dT}{dx}\bigg|_{x=0}<0}$, $\displaystyle{\frac{dT}{dx}\bigg|_{x=l}>0}$이므로 사잇값 정리에 따라 (2)를 만족하는 $x_0\in[0,l]$는 반드시 존재한다.
이계 도함수를 구해서 $x=x_0$에서 어떤 극값을 가지는가 판정해 보자.
$$\frac{d^2T}{dx^2}=\frac{a^2}{v_1(x^2 +a^2)\sqrt{x^2 + a^2}} + \frac{ b^2}{v_2((l-x)^2 +b^2)\sqrt{(l-x)^2 + b^2}}>0\tag{3}$$
이계 도함숫값이 양수이므로 $x=x_0$에서 극솟값을 가지고 이 값이 최솟값이다.
(2)를 만족하는 $x_0$를 간단하게 나타내기 어렵다.
$$\frac{x}{\sqrt{x^2 + a^2}} =\sin\theta_1$$
$$\frac{ l - x}{\sqrt{(l-x)^2 + b^2}}=\sin\theta_2$$
위에 있는 삼각비를 써서 (2)를 다시 정리하면 아래와 같다.
$$\therefore \frac{dT}{dx}=\frac{\sin\theta_1}{v_1} - \frac{\sin\theta_2}{v_2}=0 \tag{4}$$
따라서 스넬의 법칙은 아래와 같은 식으로 표현할 수 있다.
$$\frac{\sin\theta_1}{v_1}=\frac{\sin\theta_2}{v_2}$$
$$\frac{n_1\sin\theta_1}{c}=\frac{n_2\sin\theta_2}{c} $$
$$n_1\sin\theta_1=n_2\sin\theta_2$$
https://en.wikipedia.org/wiki/Snell%27s_law
Snell's law - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search The relation between the angles of incidence and refraction of waves crossing the interface between isotropic media Refraction of light at the interface between two media of different
en.wikipedia.org