2020학년도 서울대 면접 수학 기출문제_01
자연수 $n$에 대하여 다음 조건을 만족하는 원 $A_n$을 생각해보자.
(1) $A_1$의 중심은 $(0,0)$이고 반지름은 4이다.
(2) $A_n$의 중심은 $\displaystyle{\bigg( \sum_{i=1}^{n-1}\frac{15}{2^i},0 \bigg)}$이고 반지름은 $\displaystyle{\frac{8}{2^n}}$이다. (단, $n \geq 2$)
두 원 $A_n , A_{n+1}$과 각각 만나고 $y$절편이 최대가 되는 직선을 $l_n$이라 하자.
1-1. 직선 $l_n$의 방정식을 구하시오.
1-2. 직선 $l_n$의 $y$절편을 $a_n$이라 할 때, 극한 $\displaystyle{\lim_{n\rightarrow \infty}a_n}$의 값을 구하시오.
풀이
1-1. 원 $A_n$의 중심은 등비수열의 합으로 주어졌고 반지름은 등비수열로 주어져 있다.
먼저 중심의 $x$좌표를 계산해 보자.
$$x_n=\sum_{i=1}^{n-1} \frac{15}{2^i}=\frac{15}{2}\bigg(\frac{1-1/2^{n-1}}{1-1/2}\bigg)=15\bigg(1-\frac{1}{2^{n-1}}\bigg)$$
귀납적을 해결하기 위해 $n=2$일 때를 생각해 보자.
원 $A_2$의 중심은 $\displaystyle{\bigg( \frac{15}{2},0\bigg)}$이고 반지름은 $2$이다.
이제 $l_1$의 방정식을 구해보자.
그림을 그려보면 아래와 같이 두 원 $A_1 ,A_2$의 공통 내접선이 기울기가 음일 때 $y$절편이 최대가 된다.
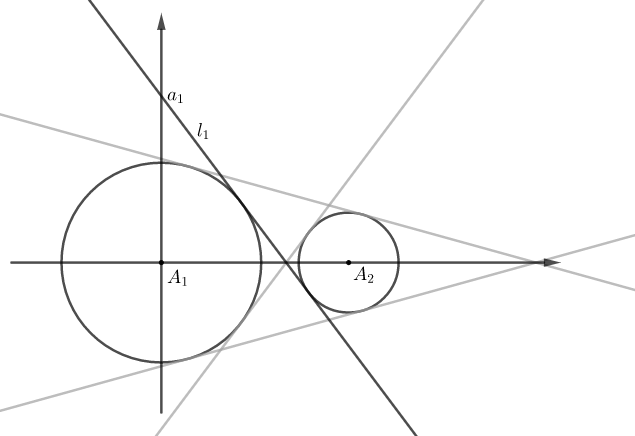
$l_1$의 $x$절편을 중심의 $x$좌표를 $2:1$로 내분하므로 $5$이다. 피타고라스 정리를 써서 기울기가 $\displaystyle{-\frac{4}{3}}$임을 알 수 있다.
$$l_1:\quad y=-\frac{4}{3}(x-5)$$
$$a_1=\frac{20}{3}$$
중심은 $\displaystyle{\frac{15}{2^n}}$씩 평행이동하고 반지름도 등비수열을 이루므로 $n$과 상관없이 직선 $l_n$과 $l_{n+1}$은 서로 평행이다. 따라서 모두 기울기가 같다.
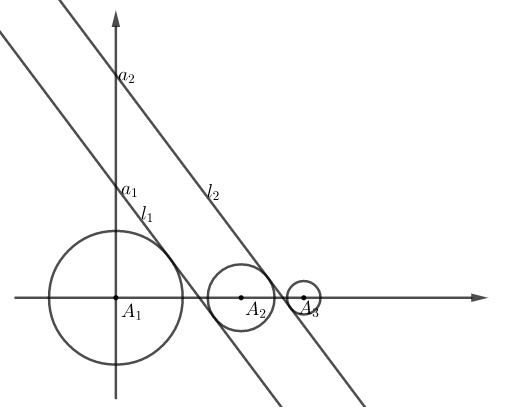
정리하면 직선 $l_n$은 기울기가 $\displaystyle{-\frac{4}{3}}$이고 $x$절편은 두 원 $A_n , A_{n+1}$의 중심을 $2:1$로 내분하는 점이다.
$$x_n =18 -\frac{15}{2^{n-1}}, \quad \quad x_{n+1}=15-\frac{15}{2^n}$$
$2:1$로 내분하는 점은
$$\frac{1}{3}(2x_{n+1}+x_n)=\frac{1}{3}\bigg(45- \frac{15}{2^{n-1}}\bigg)= 15-\frac{5}{2^{n-1}}$$
$l_n$의 방정식은
$$y= - \frac{4}{3} \bigg( x-15+\frac{5}{2^{n-1}} \bigg)$$
따라서
$$a_n = \frac{4}{3} \bigg(15- \frac{5}{2^{n-1}} \bigg)$$
마지막으로 구하고자 하는 극한값을 계산하면
$$\displaystyle{\lim_{n\rightarrow \infty}a_n}=20$$
$\blacksquare$
admission.snu.ac.kr/undergraduate/notice?md=v&bbsidx=127422
2020학년도 서울대학교 입학전형 선행학습 영향평가 - 공지사항 - 대학 - 입학 - 서울대학교 입학�
아래 첨부파일을 확인하시기 바랍니다.
admission.snu.ac.kr