'에라토스테네스' 지구 둘레를 재다
우리가 살고 있는 지구의 둘레는 얼마나 될까? 가장 처음으로 지구 둘레를 측정한 사람은 고대 그리스 학자인 에라토스테네스(Eratosthenes, B.C. 275?~B.C. 194?)로 알려져 있다. 그는 소수를 찾아가는 방법인 '에라토스테네스 체'로도 알려져 있다. 과연 어떻게 2천200여 년 전에 지구의 둘레를 측정했을까?
이집트 '시에네(Syene)'라는 도시에 우물이 있었다. 하지 정오가 되면 햇살이 이 우물 바닥까지 도달하는 것을 알았다. 달리 말하면 태양 빛이 지구와 수직을 이룬다는 사실을 알아낸 것이다. 다음으로 시에네에 북쪽에 있는 '알렉산드리아'에 수직으로 세운 막대가 하지 정오에 태양과 $7.2^\circ$를 이루고 있음을 알아냈다. 그 당시 상인들이 이동하는 데 걸리는 날수를 바탕으로 시에네에서 알렉산드리아까지 거리는 5000 스타디아(그리스 길이 단위)로 계산했는데 오늘날 미터법으로 바꾸면 대략 925Km이다. 마지막으로 지구둘레 $L$을 아래와 같이 계산하였다.
$$L\;\;:\;\;925Km=360^\circ\;\;: \;\;7.2^\circ$$
$$L=925Km \times \frac{360^\circ}{7.2^\circ}=46,250Km$$

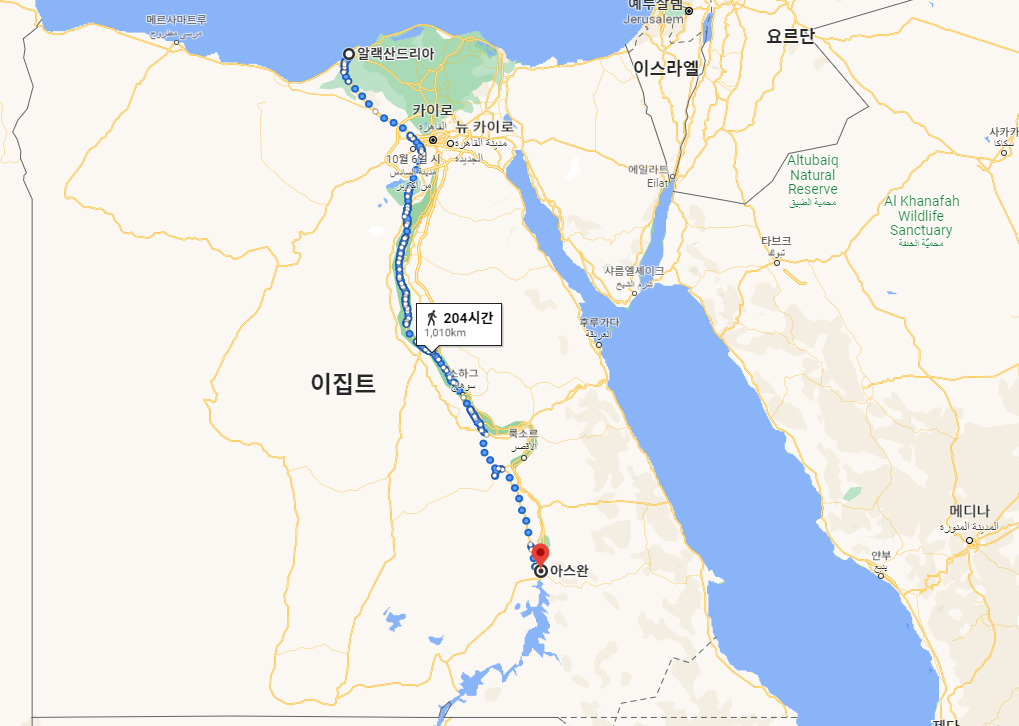
현재 지구 둘레는 약 40,075Km로 측정되고 있다고 하니 상당히 정확하다고 할 수 있다. 시에네와 알렉산드리아를 오가는 상인들의 속력을 조금 더 정확하게 추정했다면 더욱 정확한 값을 얻었을 것이다. 더 정확한 거리를 찾고자 구글 지도를 찾아 보았다. 안타깝게도 알렉산드리아는 여전한데 시에네란 도시는 검색되지 않고 다른 이름인 아스완이 나온다. 아마도 도시 이름이 바뀐 것이 아닐까 싶다. 사람들이 걷는 속력은 크게 달라지지 않았겠지! 낙타를 타고 갔으려나? 아무튼 요즘 지도로 검색하면 아스완에서 걸어서 204시간 약 1,010Km로 나온다. 아스완이 고대 시에네인지는 모르겠다. 직선 거리로 계산하면 대충 925km쯤 되지 않을까?
실제 계산과정을 들여다보면 지금은 초등학생도 할 수 있는 계산이다. 하지만 누군가로부터 배우지 않고서 이런 생각을 할 수 있는 사람은 현대에도 많지 않을 것이다. 고대 그리스 사람이 그가 지구가 평평하지 않고 둥글다고 생각했다는 사실도 놀라운 일이다. 그보다 천 년 후인 중세를 살던 이들도 지구는 평면이라 배를 타고 멀리 나가면 낭떠러지로 떨어진다고 생각하는 사람이 매우 많았다.
생각하는 힘이 얼마나 큰가를 알려주는 좋은 예이다. 수학은 인간을 다른 어떤 동물보다 위대하게 만드는 학문임이 분명하다.
10개국이 뭉쳐 지구 둘레 계산 – Sciencetimes
www.sciencetimes.co.kr