대수 막대로 수학 공부
지난해부터 중학교에서 수학을 가르친다. 중학교 교과 내용은 고등학교보다 쉽지만 가르치는 일은 그만큼 쉽지 않다. 아무래도 학생들이 처음 접하는 내용이 많기 때문이다. 음수라는 개념도 그렇고 숫자가 아닌 문자를 써서 만든 식을 다루는 것도 처음이다. 요즘 식의 계산을 가르치고 있다. 다항식을 더하고 빼고 곱하고 나누는 일은 수학을 본격적으로 공부하기 위해서 만드시 필요한 일이다.
수학의 바탕인 대수학
대수학은 영어로는 Algebra이다. 한자로 代數學로 적는데 직역하면 수를 대신하는 학문이다. 수를 대신하는 문자로 만든 식을 다루는 일을 하지 않고서 수학을 공부하는 것은 상상할 수 없다. 이런 대수를 조금 쉽게 이해할 수 있도록 돕는 도구로 대수 막대가 있다. 고등학교에서는 별 관심을 두지 않았지만 중학교 수업을 하면서 관심을 두게 되었다. 수학 교구를 만드는 회사마다 조금씩 다른 제품을 내놓고 있지만 기본적인 개념은 차이가 없다. 아래와 같이 세 종류로 이루어진 제품을 예로 들겠다.

이 막대가 무엇을 나타내는가를 정해보자. 다항식의 덧셈을 다룰 것이므로 빨간 막대는 한 변의 길이가 $x$인 정사각형으로 넓이 $x^2$, 녹색 막대는 넓이가 $1\times x$인 직사각형으로 $x$, 마지막 노란 막대는 한 변의 길이가 $1$인 정사각형으로 넓이 $1$을 나타낸다고 하자.

$$x^2 +x^2 +x^2 =3x^2$$
다항식에서 계수가 자연수라면 같은 것을 더한 개수를 나타낸다는 개념을 아주 간단하게 설명할 때 아주 유용하다.

이제 위와 같이 막대로 $4x^2 +3x+5$를 나타낼 수 있다.

$3x^2 +2x+6$을 대수 막대로 나타내면 다항식의 덧셈을 동류항의 계수를 더하는 것으로 계산해야 한다는 개념을 쉽게 설명할 수 있다.
$$(4x^2 +3x+5)+(3x^2 +2x+6)=7x^2+5x+11$$
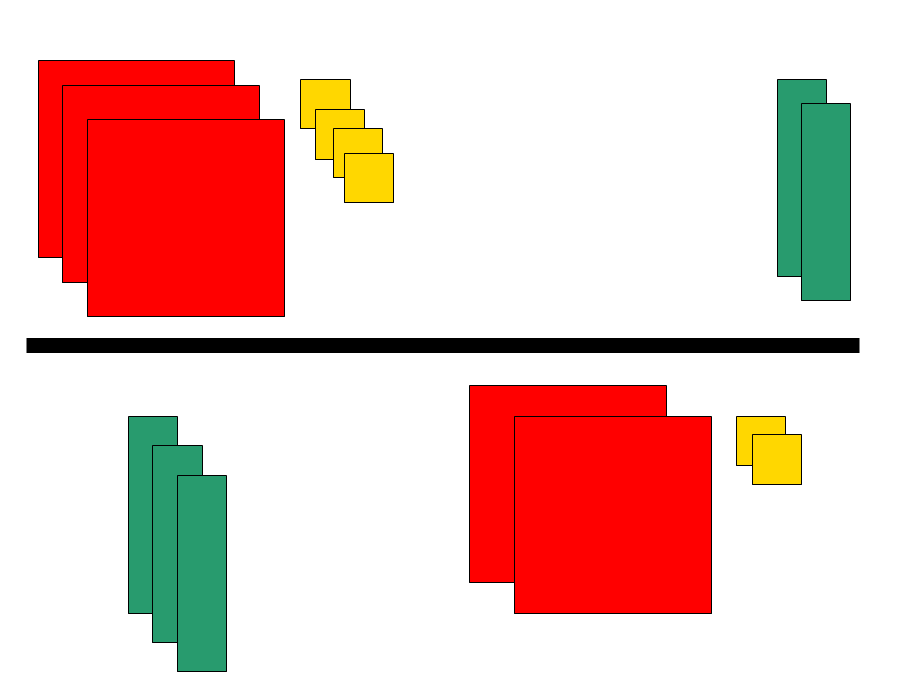
제품에 따라서 앞 뒤에 있는 색이 달라서 음수인 계수는 뒤집어서 나타낼 수 있다. 색으로 나타낼 수 없다면 구분선을 긋고 위쪽은 양수인 항을 아래쪽은 음수인 항을 배치하여 설명할 수 있다. 예를 들면 아래와 같이 배치한 대수막대는
$$(3x^2 -3x+4)+(-2x^2 +2x-2)$$를 나타낸다.
언젠가 대수 막대를 사용한 지도법을 정리하고 싶은데 당장 필요해서 며칠 전에 급하게 영상을 하나 만들었다.