일차함수
함수는 수학에서 매우 중요한 개념이다. 중학교 2학년 때, 처음으로 교과서에서 함수와 만난다. 중학교 교과서엔 다음과 같이 함수를 소개한다.
두 변수 $x,y$에 대하여, $x$의 값이 변함에 따라 $y$의 값이 하나씩 정해지는 관계가 있을 때, $y$를 $x$의 함수라고 한다.
중학생 수준에서 변수 사이의 관계를 다루는 일은 쉽지 않다. 다루기 쉬운 일차함수만 나오는 까닭이다. 일차함수는 간단하지만 결국 다른 함수를 이해하는 바탕이 되므로 공을 들여 공부해 두어야 한다.
해수면으로부터 높이가 $1km$씩 올라갈 때마다 온도가 $6^\circ C$씩 내려간다고 한다. 해수면 온도가 $0^\circ C$일 때, 높이 $x km$인 곳의 온도 $y^\circ C$를 식으로 나타내 보자. 표를 만들면 아래와 같다.
| $$x km$$ | $$0$$ | $$1$$ | $$2$$ | $$\cdots $$ | $$x$$ | $$\cdots $$ |
| $$y^\circ C$$ | $$0$$ | $$-6$$ | $$-12$$ | $$\cdots $$ | $$-6x$$ | $$\cdots $$ |
1학년에서 배운 정비례임을 알 수 있다. $$y=-6x$$ 해수면 온도가 ${12}^\circ C$라면 아래와 같다. $$y=-6x+12$$ 이와 같이 함숫값 $f\left(x\right)$를 구하는 식이 일차식인 함수를 일차함수라고 한다. 일차함수는 정비례를 나타내는 식인 $y=ax$를 평행이동한 그래프를 가진다. 따라서 $x$의 값이 수 전체이면 일차함수의 그래프는 모두 직선으로 나타남을 알 수 있다.
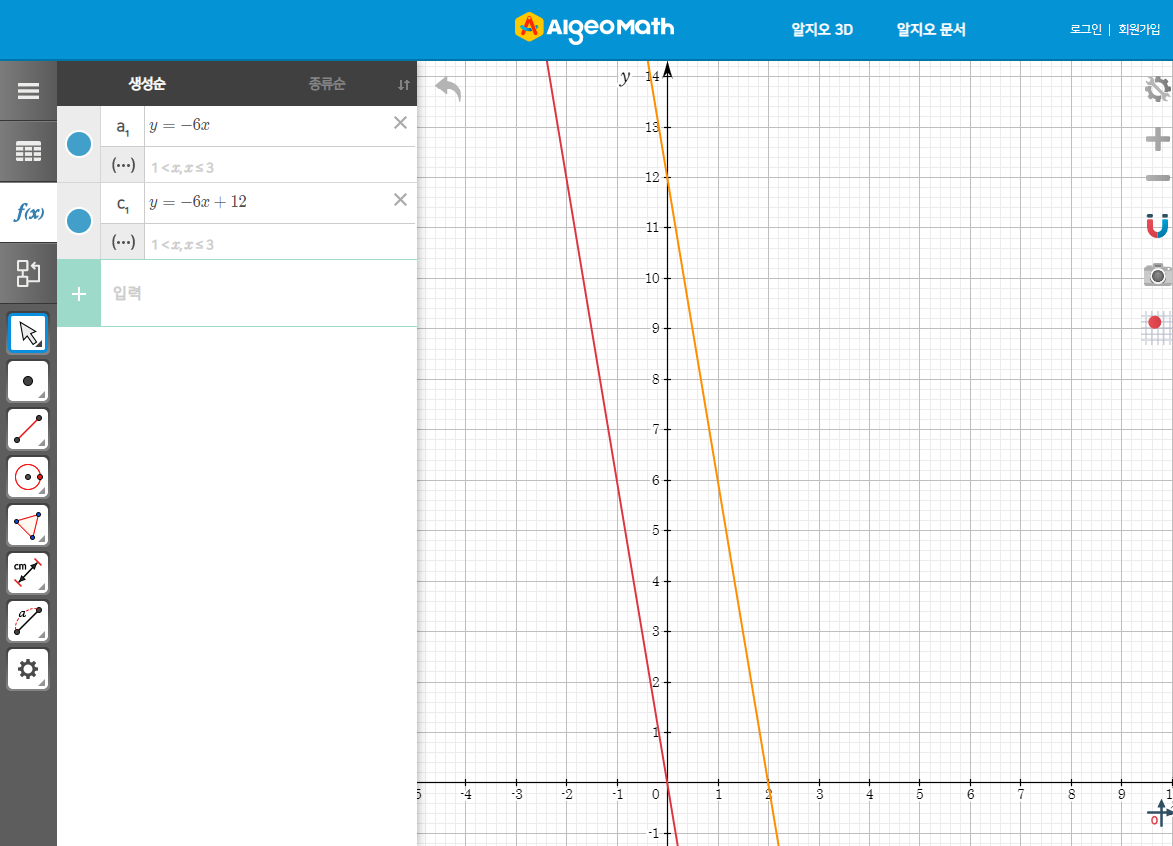
일차함수 그래프의 절편과 기울기
일반적으로 함수의 그래프가 $x$축과 만나는 점의 $x$좌표를 $x$절편, $y$축과 만나는 점의 $y$좌표를 $y$절편이라고 한다.
일차함수는 $y=ax+b$로 나타낼 수 있다.
일차함수 그래프의 $x$절편과 $y$절편을 구하는 방법을 알아보자. $x$축과 만나는 점의 $y$좌표는 모두 $0$이다. 따라서 $x$절편은 $y=0$을 대입하여 구할 수 있다. 마찬가지로 $y$축과 만나는 점의 $x$좌표는 모두 $0$이므로 $y$절편은 $x=0$을 대입하여 구할 수 있다. 특히, $y$절편은 $b$임을 알 수 있다.
일차함수 $y=-3x+6$의 그래프의 $x$절편과 $y$절편을 구해보자.
먼저, $y=0$을 대입하자. $0=-3x+6$에서 $3x=6$이므로 $x=2$이다. 따라서 $x$절편은 $2$이다. $x=0$을 대입하여 $y$절편은 $6$을 구할 수 있다.
모든 일차함수는 상수항 $b$가 $y$절편임을 기억하자.
다음으로 가장 중요한 기울기를 알아보자.
직선이 기울어진 정도를 나타낼 때 수평선과 이루는 각의 크기를 사용할 수 있다. 하지만 각을 정확하게 재는 일은 생각보다 쉽지 않다. 다행스럽게 데카르트 님이 우리에게 좌표평면이란 큰 선물을 선사하였다. 좌표평면에 그려진 직선이 기울어진 정도는 수평과 수직으로 변하는 양으로 아주 간단하게 나타낼 수 있다.
중학교 교과서에선 $x$의 값의 증가량에 대한 $y$값의 증가량의 비율로 약속하고 있다. 그런데 모든 일차함수 $y=ax+b$는 그 비율이 $a$로 일정하다. 고등학교부터 증가량은 기호로 $\Delta$를 써서 표기하고 미적분에선 증분(increment)으로 부른다.
일차함수 $y=ax+b$ 위의 서로 다른 두 점 $(x_1 ,y_1)$과 $(x_2,y_2)$가 있다고 하자.
$$\frac{y_2-y_1}{x_2-x_1}=\frac{(ax_2+b)-(ax_1+b)}{x_2-x_1}=\frac{a(x_2-x_1)}{x_2-x_1}=a$$
$$\text{기울기}=a=\frac{y\;\text{값의 증가량}}{x\;\text{값의 증가량}}=\frac{\Delta y}{\Delta x}$$
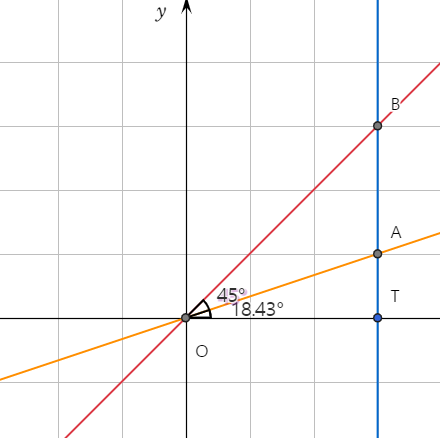
그림 1에서 두 직선이 기울어진 정도는 각각 $45^{\circ}$나 $18.43^{\circ}$보다는 $\displaystyle{\frac{\overline{TB}}{\overline{OT}}=\frac{3}{3}=1}$과 $\displaystyle{\frac{\overline{TA}}{\overline{OT}}=\frac{1}{3}}$으로 나타내는 것이 편할 때가 많다.
※ 여기서 증가량은 부호가 있는 수임을 명심해야 한다. 즉, $-2$만큼 증가한다는 것은 $2$만큼 감소함과 같음을 알아야 한다.