도형의 닮음
도형이 모양은 같고 크기만 다를 때 서로 닮았다고 부른다. 사진과 같이 똑같은 모양이 크기만 달라지면서 반복되는 그림을 본 적이 있을 것이다. 시어핀스키 삼각형과 같은 도형을 프랙털 도형이라고 부른다. 영재 학급과 비슷한 프로그램에 참가한 일이 있다면 한 번쯤은 프랙털 도형을 만났을 것이다.

이집트는 파라오의 무덤인 거대한 피라미드가 있다. 고대 그리스 수학자 탈레스는 피라미드 가운데 가장 높다는 푸쿠 왕의 피라미드의 높이를 측정했다고 한다. 그는 어떻게 측정했을까?

태양은 지구와 워낙 멀리 떨어져 있으므로 햇빛은 모든 방향으로 평행하게 비친다고 가정하자. 아래 그림에서 피라미드와 막대의 그림자, 막대의 길이는 쉽게 측정할 수 있다. 따라서 피라미드의 높이는 굳이 꼭대기까지 올라가지 않아도 길이를 알 수 있다. 알고 보면 아주 간단한 원리이지만 탈레스는 기원전 6세기 사람인 것을 생각하면 대단한 발견이다. 뭐든 남들보다 먼저 최초로 하는 것은 어렵다.

중학교 2학년 수학에서 처음으로 닮음을 배운다. 중학교 과정이 대부분 그렇듯이 처음 배울 때는 간단해 보이지만 깊이 들어가면 어렵고 복잡해진다. 닮음도 그냥 외워서 답만 구하는 연습만 하면 풀기 어려운 문제가 많은 단원이다.
한 도형을 일정한 비율로 확대 또는 축소하여 만든 도형이 다른 한 도형과 합동이 될 때, 그 두 도형은 서로 닮음인 관계에 있다고 한다.
도형을 확대하거나 축소하는 것은 한 점을 중심으로 생각하면 더 쉽게 이해할 수 있다. 예를 들어 서로 닮음비가 $a$인 삼각형은 점 $O$를 중심으로 확대하거나 축소한다고 생각할 수 있다.

$$\overline{OA}:\overline{OD}=\overline{OC}:\overline{OF}=\overline{OB}:\overline{OE}=1:a\tag{1}$$
$|a|>1$이면 확대, $|a|=1$이면 합동, $|a|<1$이면 축소한 도형이다. 또한 아래와 같은 관계를 만족한다.
$$\overline{AB}//\overline{DE},\;\;\overline{AC}//\overline{DF},\;\;\overline{BC}//\overline{EF}\tag{2}$$
교과서 기호와 조금 다르지만 닮음 기호(∽)를 아래와 같이 적는다.
$$\triangle ABC \sim \triangle DEF$$
아래와 같이 두 삼각형에서 대응하는 세 변의 길이는 (1)과 같은 비율을 가진다.
$$\overline{AB}:\overline{DE}=\overline{AC}:\overline{DF}=\overline{BC}:\overline{EF}=1:a\tag{3}$$
또한 두 삼각형이 닮음이면 (2)에 따라서 대응하는 세 각의 크기는 서로 같다.
$$\angle A = \angle D,\;\;\angle B= \angle E,\;\;\angle C= \angle F\tag{4}$$
두 평면도형이 서로 닮음이면
1. 대응하는 변의 길이는 비가 일정하다.
2. 대응하는 각의 크기는 각각 같다.
3. 닮음비가 $m:n$이면 넓이의 비는 $m^2 :n^2$이다.
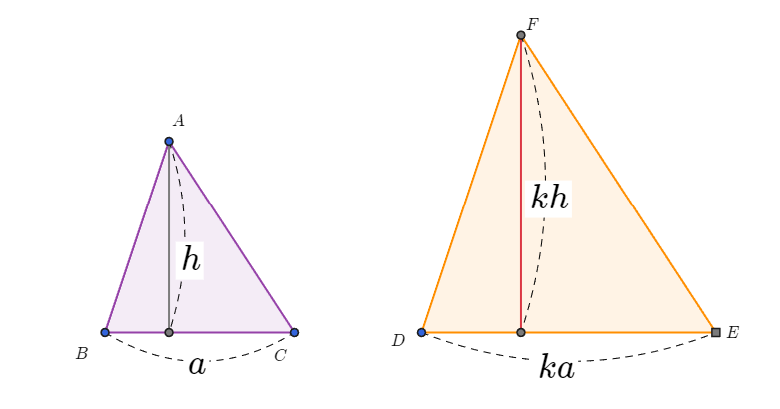
닮음비가 $1:k$인 두 삼각형은 넓이의 비가 $1:k^2$이므로 3을 쉽게 이해할 수 있다. 모든 다각형은 삼각형을 잘라서 생각할 수 있음을 기억하자.
$$\triangle ABC= \frac{ah}{2}$$
$$\triangle DEF= \frac{1}{2}\times (ka) \times (kh)= \frac{ah}{2}k^2=k^2 \triangle ABC$$
$$\triangle ABC: \triangle DEF=1:k^2$$
$\displaystyle{k= \frac{n}{m}}$이면 3과 같은 모양을 얻을 수 있다.
두 입체도형이 서로 닮음이면
1. 대응하는 모서리의 길이는 비가 일정하다.
2. 대응하는 면은 서로 닮은 도형이다
3. 닮음비가 $m:n$이면 부피의 비는 $m^3 :n^3$이다.
닮음변환 | Algeomath
닮음변환 | Algeomath, 알지오매스, 도형학습용 소프트웨어 , 도형
www.algeomath.kr


