중학교 2학년 도형의 성질 총정리
지나고 나면 도대체 그땐 왜 몰랐을까라는 생각이 들 때가 많다. 내가 지금 알고 있는 것을 그때도 알았더라면! 고등학생이 되어 중학교 2학년 수학책을 다시 본 적이 있는가? 있다면 어떤 느낌이었나? 아 이 쉬운 걸 왜 어려워했지라는 느낌이라면 성공이고 이런 쓸데없는 걸 왜 하냐는 느낌이라면 실패다.
중학교 2학년 수준에서 알아야 하는 도형의 성질을 정리해 본다. 적어도 아래에 등장하는 그림이 사진처럼 머리 속에 저장되어 있다면 성공이다. 설명까지 곁들일 수 있다면 그야말로 대성공이다. 영어로 된 자료를 보고 싶다면 영어 이름을 클릭하면 된다.
이등변 삼각형(Isosceles Triangle): 두 변의 길이가 같은 삼각형

삼각형에서 각은 건너편에 있는 변의 길이에 따라 결정된다. 당연히 이등변 삼각형의 밑각은 서로 같다. 역으로 두 각이 같은 삼각형은 이등변 삼각형이다. 꼭지각인 $\angle A$의 이등분선은 밑변 $BC$를 수직 이등분한다.
삼각형의 외심(circumcenter): 외접원의 중심
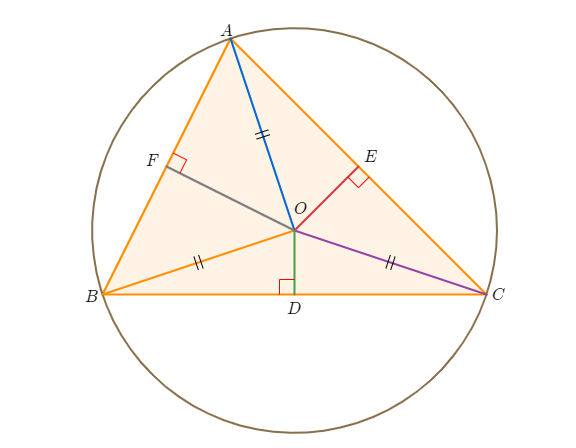
당연히 외심에서 세 꼭짓점에 이르는 거리가 같다. 어떻게 찾을까? 세 변의 수직 이등분선은 한 점(외심)에서 만난다. 따라서 두 변의 수직 이등분선이 만나는 점을 찾으면 된다.
삼각형의 내심(incenter): 내접원의 중심

내심에서 세 변에 이르는 거리가 같다. 각의 이등분이 만나는 점을 찾으면 된다. 삼각형 넓이 $S$를 구하는 새로운 공식을 하나 찾을 수 있다.
$$S=\frac{1}{2}(a+b+c)r$$
평행사변형(parallelogram): 두 쌍의 대변이 서로 평행인 사각형

평행사변형이란 말 다시 말해 두 쌍의 대변이 서로 평행하다는 조건과 다음에 있는 네 가지 조건은 모두 같은 조건이므로 구별하지 않아도 된다. (1) 두 쌍의 대변의 길이가 서로 같다. (2) 두 쌍의 대각의 크기가 서로 같다. (3) 두 대각선이 서로를 이등분한다. (4) 한 쌍의 대변이 평행하고 길이가 같다.
직사각형(rectangle): 네 각의 크기가 같은 사각형

직사각형은 평행사변형이다. 직사각형은 두 대각선의 길이가 서로 같다.
마름모(rhombus): 네 변의 길이가 같은 사각형

마름모는 평행사변형이다. 마름모는 두 대각선이 서로를 수직 이등분한다.
정사각형(square): 네 변의 길이가 같고 네 각의 크기가 같은 사각형
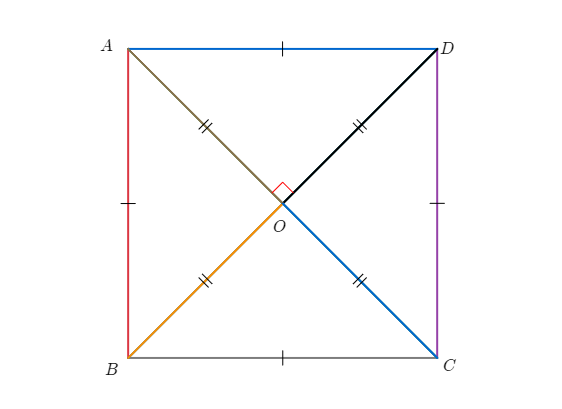
마지막으로 정사각형은 직사각형이면서 마름모이다. 모두 합동인 직각 이등변 삼각형 넷으로 나눌 수 있다. 색종이를 상상하면 된다.