삼각형의 닮음을 정리하자
한 삼각형을 일정한 비율로 확대하거나 축소한 것이 다른 삼각형과 합동이 된다면 이 두 삼각형은 서로 닮음인 관계에 있다. 닮음인 도형은 서로 모양은 같고 크기만 다르다고 할 수 있다. 두 삼각형이 닮음인 관계에 있다면 당연히 세 쌍의 대응각은 크기가 각각 서로 같고 대응변은 길이의 비가 모두 같아야 한다. '
$$\triangle ABC \sim \triangle DEF$$
$$\angle A=\angle D,\;\;\angle B=\angle E,\;\;\angle C= \angle F$$
$$\overline{AB}:\overline{DE}=\overline{BC}:\overline{EF}=\overline{CA}:\overline{FE}$$

삼각형의 닮음 조건
삼각형의 결정 조건을 생각하면 삼각형의 합동과 마찬가지로 닮음을 확인할 때 세 각과 세 변을 모두 확인할 필요가 없음을 알 수 있다. 삼각형이 주어졌을 때 확대하거나 축소한 삼각형을 직접 손으로 그려보면 닮음 조건을 쉽게 찾을 수 있다. 닮음을 확인할 때 반드시 살펴야 하는 조건은 아래와 같다.
1) 세 쌍의 대응변의 길이의 비가 같다.
$$\overline{AB}:\overline{DE}=\overline{BC}:\overline{EF}=\overline{CA}:\overline{FE}\tag{SSS}$$
2) 두 쌍의 대응변의 길이의 비가 같고, 그 끼인각의 크기가 같다.
$$\overline{AB}:\overline{DE}=\overline{BC}:\overline{EF},\;\;\angle B=\angle E \tag{SAS}$$
3) 두 쌍의 대응하는 각의 크기가 각각 같다.
$$\angle A=\angle D,\;\;\angle B=\angle E\tag{AA}$$
닮음인 관계에 있는 두 삼각형은 세 대응각의 크기가 모두 같다. 따라서 적당히 이동하면 언제나 아래 그림과 같이 한 쌍의 대응변이 평행이 되도록 만들 수 있다.
삼각형과 평행선
닮음인 두 삼각형에서 세 쌍의 대응각은 각각 크기가 같다. 따라서 하나의 각을 포개면 대응변 두 쌍이 일치하고 다른 한 쌍은 평행이 된다.(두 삼각형이 합동인 경우는 제외)
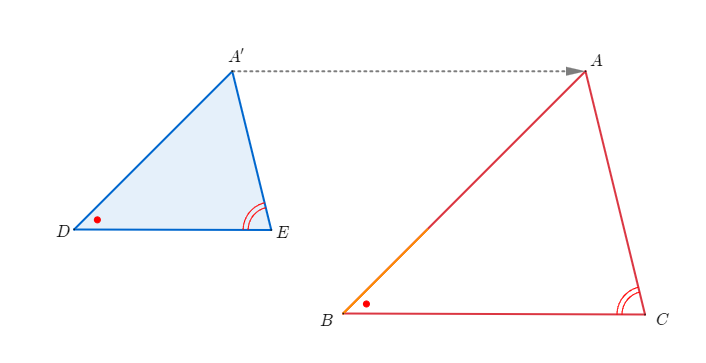
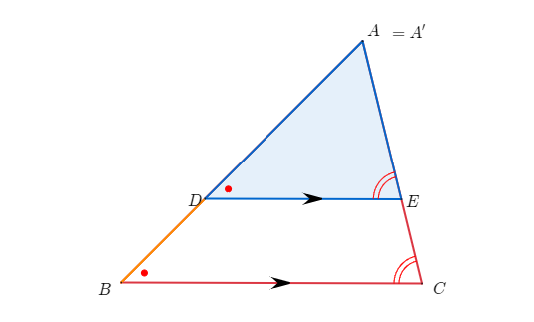
아래 그림에서 몇 가지 중요한 선분의 길이의 비를 찾을 수 있다.

두 변에 평행인 직선을 긋는다면 $$\overline{BC}//\overline{DE},\;\;\overline{AB}//\overline{EF}$$
$\square DBFE$는 평행사변형이므로 $\overline{DB}=\overline{EF}$이다.
$$ \triangle ABC \sim \triangle ADE \sim \triangle EFC$$
$\triangle ABC\sim \triangle ADE$에서 $$\overline{AB}:\overline{AD}=\overline{AC}:\overline{AE}=\overline{BC}:\overline{AE}\tag{1}$$
$\triangle ABC\sim \triangle EFC$에서
$$\overline{AB}:\overline{DB}=\overline{AC}:\overline{EC}\tag{2}$$
$\triangle ADE\sim \triangle EFC$에서
$$\overline{AD}:\overline{DB}=\overline{AE}:\overline{EC}\tag{3}$$
한편 (1)은 아래 그림과 같이 뒤집어서 포갠 경우에도 성립함을 쉽게 알 수 있다.

평행이동만 한 문제보다 뒤집어서 포갠 문제가 조금 더 생각을 해야한다. 하지만 결국은 같은 유형의 문제이다. 이렇게 같은 유형인 문제를 따로 구분하여 공식을 따로 정리하는 모습을 자주 본다.
다양한 경우에 따른 공식을 따로 외우기보다 공통되는 성질을 탐구하는 것이 옳은 방향이다. 닮음인 삼각형을 찾기만 하면 모든 것이 해결된다. 많은 문제를 풀다 보면 저절로 공식이 외워지기도 한다. 하지만 공식에만 의지해서 문제를 빨리 답만 구하는데 급급하지는 말자.
https://www.algeomath.kr/algeomath/app/key/a050b51a617611ed8d6ef220cd50c085/view.do
삼각형과 평행선 | Algeomath
삼각형과 평행선 | Algeomath, 알지오매스, 도형학습용 소프트웨어 , 도형
www.algeomath.kr
닮음을 이용하는 문제 대부분은 아래 그림과 같이 평행선을 이용하면 쉽게 해결할 수 있다. 평행인 직선이 없으면 평행인 보조선을 긋는 문제일 것이다.

$$\triangle ABC \sim \triangle ADE\sim \triangle AGF$$
각의 이등분선과 평행선
각의 이등분선이 들어 있는 문제가 평행인 보조선을 긋는 대표 문제이다. 이런 문제는 보조선만 그으면 아주 간단하게 해결되지만 보조선이 없으면 좀처럼 실마리가 잡히지 않는다.
1) 내각의 이등분선

직선 $AD$가 내각인 $\angle A$의 이등분선이라고 하자.
꼭지점 $C$를 지나고 직선 $AD$에 평행인 직선 $AB$와 만나는 점을 $E$라고 하자.
평행선 성질에 따라 $\triangle ACE$는 이등변 삼각형이다.
$$\overline{AB}:\overline{AE}=\overline{AB}:\overline{AC}=\overline{BD}:\overline{DC}$$
2) 외각의 이등분선

이것은 외각의 이등분선도 마찬가지다.
그림과 같이 직선 $AD$가 $\angle A$의 외각을 이등분한다고 하자.
꼭지점 $C$를 지나고 직선 $AD$에 평행인 직선 $AB$와 만나는 점을 $E$라고 하자.
평행선 성질에 따라 $\triangle ACE$는 이등변 삼각형이다.
$$\overline{AB}:\overline{AC}=\overline{AB}:\overline{EA}=\overline{BD}:\overline{CD}$$
둘을 굳이 구별할 필요는 없다. 각의 이등분선이 있는 문제는 이등분선과 평행인 선을 그어서 해결한다만 기억하자.