이차함수와 평행이동
이차함수는 중학교 3학년 과정에 등장한다. 이차함수의 그래프인 포물선을 평행이동하는데 이것을 정확하게 설명하기가 생각보다는 어렵다. 특히 도형의 방정식을 온전하게 지도하려면 고등학교 과정이 필요하다. 선행학습으로 이미 과정을 배운 학생도 도형의 평행이동을 완벽하게 이해하지 못하는 학생이 많다.
평행이동을 중학교 수준에서 정리해 두려고 한다. 평행이동은 초등학교 4학년과 중1에서 잠깐 등장하지만 수학적으로 정의하지 않고 그냥 배운다. 일단 중학교 1학년 교과서에 있는 설명을 보자.
평행이동은 어떤 도형 위에 있는 모든 점을 일정한 방향으로 정해진 거리만큼 옮기는 것이다.

이차함수 그래프의 평행이동
중학교 1학년에서 좌표평면을 배웠으므로 이제는 $x$축 방향과 $y$축 방향을 구분하여 다룰 수 있다.
$y=ax^2$과 $y=ax^2 +q$의 그래프
두 그래프 사이의 관계는 직관적으로도 쉽게 설명할 수 있다? 빨간 포물선 위에 있는 $y$의 값이 $ax^2$에 모두 $p$를 더했다고 생각하면 된다. 물론 이때도 파란 $y$와 빨간 $y$가 같은 문자로 적었지만 결코 같은 것이 아님을 알아야 한다.
$$y=ax^2\tag{1}$$
(1)의 우변에만 $q$를 더했다.
$$y=ax^2+q\tag{2}$$
변수를 이해하지 못해서 학생들이 함수를 어려워한다.

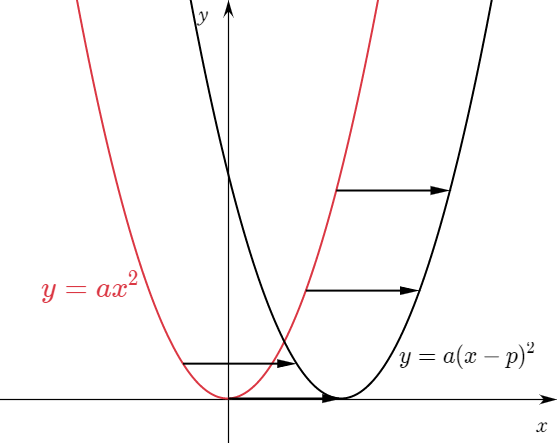
$y=ax^2$과 $y=a(x-p)^2 $의 그래프
이것은 설명하기 어렵다. $p$만큼 이동하는데 함수식은 $x-p$로 표현되기 때문이다. 알고 나면 너무나 당연한 일인데 일부 학생은 설명을 해도 이해하지 못하고 혼란스러워 한다. 오른쪽으로 이동할 때는 $+$이고 왼쪽으로 이동할 때는 $-$가 아닐까 생각하는 학생들이 있다. 그렇다고 '그냥 외워!'라고 외칠 수 없다.
어쩌면 교과과정을 벗어난 방식이지만 나름대로 설명을 달아두려고 한다. 먼저 두 함수식에 등장하는 $x,\;y$가 똑같은 수를 나타내지 않고 따로 각각 변하는 수를 나타냄을 상기하자. 다시 말해 상수 $a$와 변수 $x,y$를 구별해야 한다.
$y=ax^2$의 위에 있는 점을 $A(u,v)$라고 하면 $$v=au^2\tag{3}$$이다.
이제 $A(u,v)$을 $x$축의 방향으로 $3$만큼 평행이동한 점을 $B(x,y)$라고 하자.
$$u+3=x,\;\;v=y$$
따라서 $$u=x-3,\;\;v=y$$이다. 이것을 (3)에 대입하면
$$y=a(x-3)^2$$
이다.
마찬가지로 $y$축 방향으로 이동한 식을 찾을 수 있다.
$y=ax^2$과 $y=a(x-p)^2 +q$의 그래프
이제 $A(u,v)$을 $x$축의 방향으로 $p$, $y$축 방향으로 $q$만큼 평행이동한 점을 $B(x,y)$라고 하자.
$$u+p=x,\;\;v+q=y$$
따라서 $$u=x-p,\;\;v=y-q$$이다. 이것을 (3)에 대입하면
$$y-q=a(x-p)^2$$
이다.

고등학교 과정에서 다루는 도형의 평행이동
도형 $f(x,y)=0$를 $x$축의 방향으로 $p$, $y$축 방향으로 $q$만큼 평행이동한 도형의 방정식은 $f(x-p,y-q)=0$이다.
고교 과정에서는 점 $(x,y)$를 평행이동한 점을 $(x^{\prime},y^{\prime})$로 놓고 증명한다.
$$x+p=x^{\prime},\quad y+q=y^{\prime}$$
에서 $$f(x^{\prime}-p,y^{\prime}-q)=0\tag{4}$$이다. 그런데 (4)에서 $\prime$을 지우고 아래와 같이 쓴다. 여기서 일부 학생들이 혼란스러워 한다.
$$f(x-p,y-q)=0$$
위와 같은 결과를 알고 나면 이차함수의 그래프를 평행이동한 식은 포물선의 꼭짓점을 옮긴 식으로 생각하면 쉽게 이해할 수 있다.
https://www.algeomath.kr/algeomath/app/key/9c29e3c7fb8e11eda2b4f220ef6cc976/view.do
이차함수의 평행이동2 | Algeomath
이차함수의 평행이동2 | Algeomath, 알지오매스, 도형학습용 소프트웨어 , 도형
www.algeomath.kr