$\sqrt 2$는 무리수이다
학교에서 처음 만나는 무리수로 원주율 $\pi$를 꼽을 수 있지만 본격적으로 무리수를 배우는 단원에서 처음 만나는 무리수는 $\sqrt 2$이다. 고대 문명에서도 마찬가지였을 것이다. 피타고라스 학파는 무리수인 $\sqrt2$가 존재한다는 사실을 비밀에 부치기도 했다고 전해진다. 비밀을 바깥으로 알린 히파수스(Hippasus of Metapontum)를 벌했다는 이야기도 있다.
$\sqrt2$가 무리수임을 밝히는 증명은 여러 가지가 있다. 가장 널리 알려진 유클리드의 증명은 이미 올렸으니 이글은 조금 덜 알려진 증명으로 시작하자.
기하적 증명
$\triangle ABC$는 직각 이등변삼각형이라고 하자.
피타고라스 정리에 따라
$$m=\sqrt{n^2+n^2}=n\sqrt2$$
$$\therefore \sqrt2 =\frac{m}{n}$$
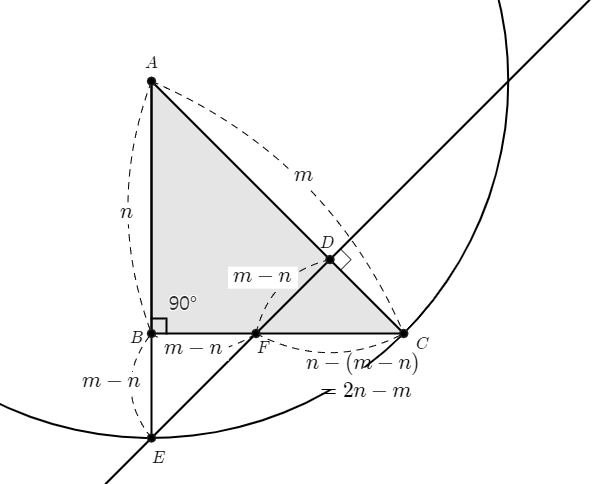
$A$를 중심으로 선분 $AC$가 반지름인 원과 직선 $AB$가 만나는 점을 $E$라고 하자.
점 $E$에서 선분 $AC$에 내린 수선을 발을 $D$라고 하고 $ED$와 $BC$가 만나는 점을 $F$라고 하자.
$$\triangle ABC\sim \triangle EBF\sim \triangle CDF$$
$$\frac{\overline{AC}}{\overline{BC}}=\frac{\overline{EF}}{\overline{BF}}=\frac{\overline{FC}}{\overline{FD}}$$
$$\therefore \frac{m}{n}=\frac{2n-m}{m-n}$$
$$\displaystyle {{\sqrt {2}}={\frac {m}{n}}={\frac {2n-m}{m-n}}={\frac {2(m-n)-(2n-m)}{(2n-m)-(m-n)}}={\frac {3m-4n}{3n-2m}}=\cdots }$$
이것은 $\sqrt2$를 기약분수로 나타낼 수 없음을 말해준다.
$\blacksquare$
대수적으로 증명
아래와 같이 대수적으로 표현할 수 있다. 이 증명도 귀류법을 쓴다.
먼저 $\sqrt2$가 유리수라고 하면 $\sqrt2=m/n$ ($m,n$은 서로소인 자연수)와 같은 꼴로 나타낼 수 있다.
다시 말하면 기약분수로 나타낼 수 있다.
이제 $m=n\sqrt2 >n$이므로
$$m-n>0.\tag{1}$$
이다. 또한 $m=n\sqrt2 <2n$이므로
$$m-n<n.\tag{2}$$
아래와 같이 정리하자.
\begin{split}m^2&=2n^2\\m^2 -nm&=2m^2-nm\\m(m-n)&=(2n-m)n\\\frac{2n-m}{m-n}&=\frac{m}{n}\end{split}
그러므로
$$\frac{2n-m}{m-n}=\sqrt2$$이다.
(1)에 따라 $\displaystyle{\frac{2n-m}{m-n}}$의 분모는 양수이고, (2)에 따라 $\displaystyle{\frac{2n-m}{m-n}}$의 분모는 $n$보다 작다.
모순이 생겼으므로 $\sqrt2$는 유리수가 아니다.
$\blacksquare$
연분수(Continued_fraction)
아래와 같이 $x$를 양의 정수인 $a_i$로 표현한 것을 연분수(Continued_fraction)라고 한다.
$$\displaystyle {x=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}}}}}}}}$$
여러 가지 표기법이 있다. 가우스는 아래와 같이 나타냈다.
$$x=a_{0}+{\underset {i=1}{\overset {3}{\mathrm {K} }}}~{\frac {1}{a_{i}}}$$
계수만 따로 아래와 같이 쓰기도 한다.
$$x=[a_0;a_1,a_2,a_3]$$
유한에만 한정하지 않고 무한 연분수를 다음과 같이 극한을 이용하여 정의한다.
$$\displaystyle {[a_{0};a_{1},a_{2},a_{3},\cdots ]=\lim _{n\to \infty }[a_{0};a_{1},a_{2},\cdots ,a_{n}]}$$
모든 유한 연분수는 유리수이며, 모든 유리수는 $[2;3,1]=[2;4]=\displaystyle{\frac{9}{4}}=2.25$ 의 경우와 같이 정확히 두 가지 유한 연분수로 나타내어진다. 오일러는 모든 유리수를 유한 연분수로 나타낼 수 있고, 역도 성립한다는 사실을 증명했다. 오일러 연분수(infinite continued fraction) 공식
모든 무한 연분수는 무리수이며, 모든 무리수는 무한 연분수로 표현할 수 있고 그 표현은 유일하다. 무한 연분수가 꼬리들이 되풀이 되면 순환 연분수라고 한다. 어떤 무리수가 순환 연분수로 표현할 수 있는 필요충분조건은 그 수가 어떤 이차방정식의 해가 되는 것이다. 즉, 이차 무리수(영어: quadratic irrational number)인 것이다.
$\sqrt2$를 연분수로 나타내기
$$\sqrt2=1+\sqrt 2- 1=1+\frac{1}{1+\sqrt2}$$
$$\sqrt2=1+\frac{1}{1+\sqrt2}\tag{3}$$
(3)을 다시 (3)에 대입한다.
$$\sqrt2=1+\cfrac{1}{1+1+\cfrac{1}{1+\sqrt2}}$$
$$\sqrt2=1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{1+\sqrt2}}}$$
$$\sqrt2=1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cdots}}}$$
되풀이 하면 무한 연분수이면서 순환 연분수임을 쉽게 확인할 수 있다. 따라서 $\sqrt2$는 이차 무리수이다.
$$\displaystyle{\sqrt2 =1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{}\ddots }}}}}}}}.}$$
$$\sqrt2=[1;2,2,2,2,\cdots]$$
몇몇 상수를 연분수로 나타내면 아래와 같다.
- $e=[2;1,2,1,1,4,1,1,6,1,1,8,\cdots]$
- $\pi=[3;7,15,1,292,1,1,1,2,1,3,1,\cdots]$
- $\varphi=[1;1,1,1,1,1,1,1,1,\cdots]$
- $\gamma=[0;1,1,2,1,2,1,4,3,13,5,1,\cdots]$
- $\sqrt{19}=[4;2,1,3,1,2,8,2,1,3,1,2,8,\cdots]$
제곱근 2는 유리수가 아니다
제곱해서 2가 되는 수가 있는가는 피타고라스 정리로 쉽게 확인할 수 있다. 아래 그림과 같이 수직선 위에 한 변의 길이가 1인 정사각형의 대각선의 길이에 해당하는 점이 존재한다. $$r^2=1^2+1^2=2$
suhak.tistory.com