푸리에 변환을 향해
혹시 주역을 아는가? 몰라도 상관없다. 꽃이 피면 반드시 지고 달이 차면 기운다. 만나면 헤어지고 헤어지면 언젠가 만나는 것이 세상 이치다. 이처럼 세상 모든 것에는 주기가 있다. 수학자 퓨리에는 모든 함수를 주기 함수로 나타낼 수 있다고 생각했다.
아래와 같이 주기함수를 더하는 일은 비교적 쉽다. 하지만 파란 그래프만 보고 아래에 있는 주기함수를 거꾸로 찾아내는 일은 매우 어렵다. 물감을 섞는 일은 아주 쉽지만 뒤섞인 물감을 색깔별로 분리하는 일은 거의 불가능하다. 이 어려운 일을 할 수 있게 돕는 것이 바로 퓨리에 변환이다.

수십 년 전에 대학 다닐 때는 별로 눈에 들어오지 않더니 오십이 훌쩍 넘은 이 나이에 갑자기 이런 것들이 궁금해진다. 그 시절에 열심히 공부했으면 인생이 달라졌으려나! 아무튼 하다 만 수학 공부가 아쉬워질 줄은 몰랐다.
다행스럽게 요즘은 이런 걸 배우러 굳이 대학까지 가지 않아도 된다. 친절하게 가르쳐 주는 자료가 차고 넘친다. 이 글은 누굴 가르치는 자료가 아니라 홀로 공부하는 과정을 기록한 것으로 보면 된다.
푸리에 급수
푸리에 급수는 주기 함수를 삼각 함수의 합으로 확장한 것이다 . 푸리에 급수는 삼각함수로 만든 급수이지만 모든 삼각함수로 만든 급수가 푸리에 급수인 것은 아니다. 삼각 함수는 다루기 쉽기 때문에 함수를 사인과 코사인의 합으로 표현하면 함수와 관련된 많은 문제를 분석하기가 더 쉬워진다.
예를 들어 푸리에 급수는 푸리에가 열방정식의 해를 찾기 위해 처음 사용했다. 이러한 응용은 삼각함수의 도함수가 단순한 패턴에 속하기 때문에 가능하다. 푸리에 급수는 대부분의 함수의 푸리에 급수에 무한히 많은 항이 있고 급수가 항상 수렴하지 않기 때문에 임의의 함수를 근사하는 데 사용할 수 없다.
예를 들어 부드러운 함수와 같이 잘 작동하는 함수에는 원래 함수로 수렴하는 푸리에 급수가 있다. 푸리에 급수의 계수는 아래 푸리에 급수의 공통 형식에 설명된 삼각 함수로 곱한 함수의 적분에 의해 결정된다. 푸리에 급수의 수렴에 대한 연구는 부분합의 동작에 중점을 둔다. 즉, 급수에서 점점 더 많은 항이 합산됨에 따라 합의 동작을 연구하는 것을 의미한다.
푸리에 급수의 계수는 아래와 같이 적분으로 정의한다.
$$\displaystyle {\begin{aligned}A_{0}&={\frac {1}{P}}\int _{-P/2}^{P/2}s(x)\,dx\\A_{n}&={\frac {2}{P}}\int _{-P/2}^{P/2}s(x)\cos \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\qquad \\B_{n}&={\frac {2}{P}}\int _{-P/2}^{P/2}s(x)\sin \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\end{aligned}}$$
푸리에 급수는 아래와 같다.
$$s(x)\sim A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left({\frac {2\pi nx}{P}}\right)+B_{n}\sin \left({\frac {2\pi nx}{P}}\right)\right)\tag{1}$$
보기
아래는 그림과 같이 그래프가 톱니 모양인 함수이다.
$$s(x) = \frac{x}{\pi}, \quad \mathrm{for } -\pi < x < \pi$$
$$s(x + 2\pi k) = s(x), \quad \mathrm{for } -\pi < x < \pi \text{ 그리고 } k \in \mathbb{Z}.$$
푸리에 급수의 계수는 아래와 같이 결정된다.
함수 $s$가 미분가능한 모든 점 $x$에서 푸리에 급수는 $s(x)$로 수렴한다.

\begin{align}s(x) &= A_0 + \sum_{n=1}^\infty \left(A_n\cos\left(nx\right)+B_n\sin\left(nx\right)\right) \\[4pt]
&=\frac{2}{\pi}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin(nx), \quad \mathrm{for} \quad x - \pi \notin 2 \pi \mathbb{Z}. \end{align}
$x$가 $\pi$에 홀수를 곱한 수일 때, 푸리에 급수는 $x=\pi$에서 s의 왼쪽과 오른쪽 극한의 절반의 합인 0으로 수렴한다. 위 보기는 바젤 문제의 해결책을 만든다.
https://en.wikipedia.org/wiki/Fourier_series
Fourier series - Wikipedia
en.wikipedia.org
퓨리에 변환이란?
대표적인 주기 함수는 파동을 나타내는 사인과 코사인 함수다. 사인과 코사인은 평행이동하면 포개어지므로 코사인 함수만 생각해도 된다. 아래는 위에 있는 파동을 모두 포개어 놓은 것이다.

주기 함수를 더한 함수가 반드시 주기 함수가 되지는 않는다. 주기 함수라고 하더라도 순수한 코사인파로 나타내는 일은 쉽지 않다. 파란색 파동에서 순수한 코사인파를 분리해 내는 기계가 바로 퓨리에 변환이다. 자세하게 알아보기 전에 일단 모양만 살펴보자.
$$\displaystyle {X(\xi )=\int _{-\infty }^{\infty }x(t)\ e^{-2\pi i\xi t}\,dt}$$
$t$는 시간, $\xi$는 주파수를 나타내는 변수라고 생각하면 된다. 아래와 같이 쓰기도 한다.
$${\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-i2\pi \xi x}\,dx$$
https://en.wikipedia.org/wiki/Fourier_transform
Fourier transform - Wikipedia
en.wikipedia.org
일단 $e^{-i\xi}$로 복소수 지수를 품고 있어서 수식이 아주 무섭게 보인다. 이렇게 뭔가 차원이 높은 일을 처리하려면 오일러 공식이 필요하다. 그래서 아래에 있는 식을 세상에서 가장 아름다운 수식이라고 부른다. 복소수는 곧 벡터라고 생각하면 이해하기 쉽다.
$$e^{i\theta}=\cos \theta+i\sin \theta\tag{2}$$
쓸모 있는 극좌표
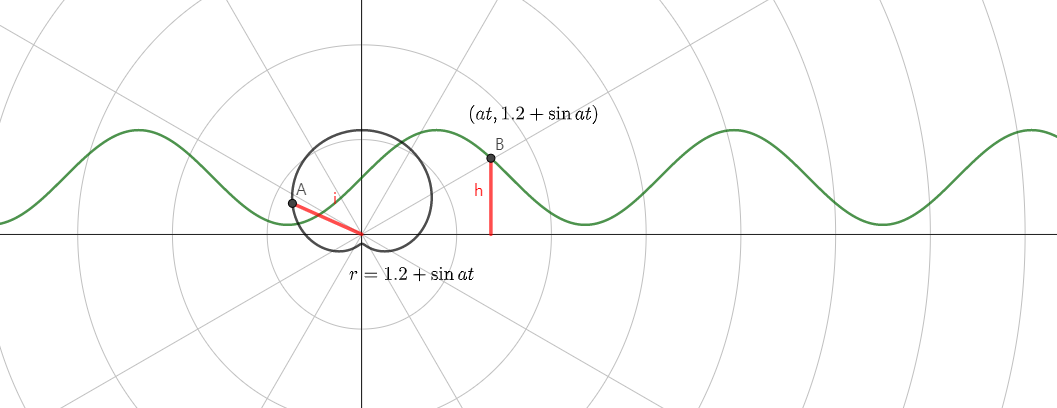
$y=2+\sin ax$는 주기가 $2\pi/a$이다. 이때 $y$의 값을 $r$이 되도록 원점을 중심으로 회전한다고 생각하자. 아래와 같이 극좌표로 변환한다고 생각하는 것이다.
$$r=2+\sin \theta$$

이제 각속도가 $a$일 때를 생각하자.
$a=1$
$a=2$

$a=4$

$a=10$

두 가지 주기가 생긴다. 하나는 파동의 마루에서 마루까지의 주기이고 다른 하나는 원점을 도는 주기이다. 각속도 $a$에 따라 한 바퀴 도는데 걸리는 시간이 달라지므로 꽃잎이 몇 장이 생기느냐가 결정된다.

두 함수의 내적을 아래와 같이 정의한다.
$$<f(t),g(t)>=\int_{a}^{b} f(t)g(t) dt$$
이제 푸리에 변환을 다시 들여다 보면 함수의 내적임을 알 수 있다.
$$\displaystyle {X(\xi )=\int _{-\infty }^{\infty }x(t)\ e^{-2\pi i\xi t}\,dt}$$
$t$는 시간을 나타내는 변수라고 생각하자.
함수 $g(t)=e^{-2\pi i\xi t}$는 반지름이 $1$인 원을 회전하는 운동을 나타낸다. 주기 $T$는 아래와 같다.
$$T=\frac{2\pi}{2\pi\xi}=\frac{1}{\xi}$$
따라서 $\xi=1/T$이므로 진동수라고 또는 주파수라고 생각하면 된다.
거칠게 말하면 푸리에 변환은 함수를 원에 감아서 특정한 주파수를 가진 파동을 분리해 내는 기계가 된다. 아래에 있는 영상이 가장 쉽게 설명하고 있어서 참고로 삼았다.
https://www.youtube.com/watch?v=Mc9PHZ3H36M
