2023학년도 카이스트 면접 수학 기출문제_3, 4
문제 3 학교장추천, 고른기회 전형
실수 순서쌍 $(a_0,b_0)$을 생각하자. 방정식 $x^2+a_0 x+b_0=0$의 실수해가 존재하지 않으면 순서쌍 $(a_0,b_0)$의 친화도를 $0$으로 정의하고, 방정식 $x^2+a_0 x+b_0=0$의 두 실수해 $a_1, b_1(a_1\geq b_1)$을 가지면(중근은 두 개로 센다) 새로운 방정식 $x^2+a_1 x+b_1=0$을 만들어 이 방정식의 실수해가 없으면 $(a_0,b_0)$의 친화도를 $1$로 정의하고, 실수해가 존재하면 두 실수해를 $a_2, b_2(a_2\geq b_2)$로 두자. 이런 과정을 반복해서 방정식 $x^2+a_k x b-k=0$가 실수해를 갖지 않는 최소의 $k$를 순서쌍 $(a_0,b_0)$의 친화도로 정의하자. 만약 이런 과정이 끝나지 않고 계속 반복된다면 순서쌍 $(a_0,b_0)$의 친화도는 정의되지 않는다고 하자.
- 순서쌍 $(-6,9)$의 친화도는 정의되는가? 정의된다면 친화도는 얼마인가? (1점)
- 순서쌍 $(-3,2)$의 친화도는 정의되는가? 정의된다면 친화도는 얼마인가?
- (2점)친화도가 정의되는 순서쌍 중 친화도의 최댓값은 얼마인가? (2점)
예시 답안
(1) $(a_0,b_0)=(-6,9)$인 경우, $(a_1,b_1)=(3,3)$이 된다. 이 경우에는 방정식 $x^2+3x+3=0$의 판별식이 $D=3^2-4\cdot3=-3<0$이므로 실수해가 없다. 따라서 $(-6,9)$의 친화도는 잘 정의되고, 그 값은 1이다.
(2) $(a_0,b_0)=(-3,2)$인 경우, $(a_1,b_1)=(2,1)$이고, $(a_2,b_2)=(-1,-1)$이다. 일반적으로 $(a_k,b_k)$가 주어졌을 때, $b_k$가 음수이면, 방정식 $x^2+a_k x b-k=0$의 판별식 $D=a_k^2-4b_k$이 항상 양수이므로 실수해가 존재한다.
근과 계수의 관계에 의해서 두 해의 곱은 $b_k$이므로 음수가 된다. 따라서 $a_{k+1}> 0> b_{k+1}$이므로 $b_{k+1}$도 다시 음수가 된다. 수학적 귀납 법에 의해서 모든 $k\geq 2$에 대해서 $(a_k,b_k)$가 존재하고 $b_k$는 음수이다. 따라서 $(-3,2)$의 친화도는 정의되지 않는다.
(3) 앞에서 관찰했듯이, $b_k$가 음수가 되는 $k$가 있으면 $(a_0,b_0)$의 친화도는 정의되지 않는다. $(a_0,b_0)$의 친화도가 정의된다고 가정하자.
만약 방정식 $x^2+a_0 x+b_0=0$이 실수해를 가지지 않으면 $(a_0,b_0)$의 친화도는 $0$이다. 방정식 $x^2+a_0 x+b_0=0$가 실수해 $a_1,b_1$을 가진다고 하자. 만약 $b_1$이 음수라면 $(a_0,b_0)$의 친화도는 정의되지 않고, $a_1\geq b_1$이므로 $a_1,b_1$은 모두 양수여야 한다.
만약 방정식 $x^2+a_1 x+b_1=0$이 실수해를 가지지 않으면 $(a_0,b_0)$의 친화도는 $1$이다. 그런데 방정식 $x^2+a_1 x+b_1=0$이 실수해를 가지면, 근과 계수의 관계에 의해서 두 해의 곱은 $b_1>0$이고 합은 $-a_1<0$이다. 따라서 두 실수해는 모두 음수가 된다.
문제 (2)에 의해서 이 경우 $(a_0,b_0)$의 친화도는 정의되지 않는다. 따라서 $(a_0,b_0)$의 친화도가 정의될 경우, 그 친화도는 $0$ 또는 $1$일 수밖에 없다. 실제 앞의 문제 (1)에서 친화도가 1이 되는 순서쌍이 있음을 확인했으므로, 친화도의 최댓값은 1이다.
$\blacksquare$
문제 4 학교장추천, 고른기회 전형
그림과 같이 직각삼각형 $ABC$가 있고 선분 $AB$의 길이는 $4$이며 선분 $BC$의 길이는 $3$이다. 직각삼각형 $ABC$가 형태를 변형하지 않으며 움직이는데, 점 $A$는 벽을 따라 바닥에 닿을 때까지 아래로, 점 $B$ 는 바닥을 따라 오른쪽으로 움직인다. 벽과 바닥이 만나는 점을 $C$ 라고 하자. (아래 문항에서 빛은 직각삼각형 $ABC$를 뚫고 지나가지 않는다.)

(1) $\angle OAB$ 를 $\theta$라고 하고 $\angle BCA$를 $\alpha$라고 하자. 오른쪽에서 수평으로 빛을 벽을 향해 비출 때 벽에 생기는 그림자의 길이를 $\theta$에 대한 함수로 나타내시오. (1점)

(2) 점 $O$와 점 $B$사이의 거리를 $x$라고 하자. 이번에는 위에서 수직으로 빛을 바닥을 향해 비춘다. 아래 그림과 같이 바닥에 생긴 그림자에서 점 $C$에 대응되는 점을 $D$라고 하자. 사다리꼴 $AODC$ 의 넓이가 최대가 될 때, $x$값을 구하시오. (2점)

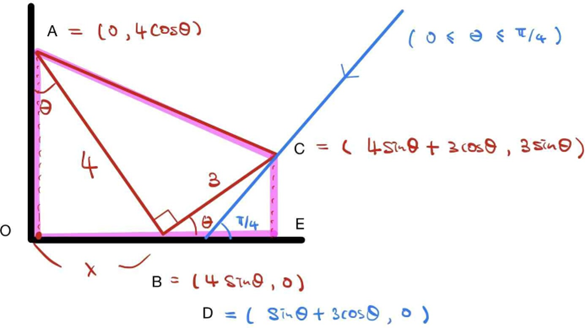
(3) 이번에는 바닥과 $45^{\circ}$ 각도로 빛을 비춘다. 아래 그림과 같이 바닥에 생긴 그림자에서 점 $C$에 대응하는 점 $D$가 점 $B$의 오른쪽에 있을 때까지만 삼각형 $ABC$를 움직인다. 사각형 $AODC$의 넓이가 최대가 될 때, 삼각형 $AOB$의 넓이를 구하시오. (2점)

예시 답안
바닥과 벽을 각각 $x$축 $y$축으로 생각한다. 선분 $AB$와 $y$축이 이루는 각이 $\theta$이고 $0\leq \theta \leq \pi/2$이다. 또한, 점 $A$의 $x$좌표는 $0$, $y$좌표는 $4\cos\theta$, 점 $B$의 $x$좌표는 $4\sin\theta$, $y$좌표는 $0$, 점 $C$의 $x$좌표는 $4\sin\theta+3\cos\theta$, $y$좌표는 $3\sin\theta$이다.

아래 그림을 통하여 점 $A$의 $y$좌표와 점 $C$의 $y$좌표는 $\theta=\alpha$일 때 같으며, $\theta <\alpha$이면 점 $A$의 $y$좌표가 더 크고, $\theta> \alpha$이면 점 $C$의 $y$좌표가 더 크다는 사실을 알 수 있다.

따라서 $$f(\theta) =\begin{cases}4\cos\theta\quad &(0\leq\theta\leq \alpha)\\ 3\sin\theta\quad &\displaystyle{\left(\alpha\leq \theta \leq \frac{\pi}{2}\right)} \end{cases}$$
(2) 아래 그림을 통하여 다음을 알 수 있다.

사다리꼴 $AODC$의 넓이 $=$ 삼각형 $ABC$의 넓이 + 삼각형 $AOB$의 넓이 + 삼각형 $BDC$의 넓이
즉, 사다리꼴 AODC의 넓이는 $$6+8\sin\theta\cos\theta +\frac{9}{2}\sin\theta\cos\theta=6+\frac{25}{4}\sin2\theta$$이다. (삼각함수의 덧셈정리를 통해 $\sin2\theta=\sin(\theta+\theta)=2\sin\theta\cos\theta$임을 유도할 수 있음)
따라서 사다리꼴 넓이는 $\theta=\pi/4$일 때 최댓값을 가지므로 $\displaystyle{x=4\sin\frac{\pi}{4}=2\sqrt2}$ 이다.
(3) 점 $D$가 점 $B$의 오른쪽에 있을 조건은 $0\leq \theta \leq \pi/4$이다. 아래 그림에서 점 $D$의 $x$좌표가 $\sin\theta+3\cos\theta$임을 알 수 있고, 사각형 $AODC$의 넓이는 사다리꼴 $AOEC$의 넓이에서 삼각형 $CDE$의 넓이를 뺀 것이므로 구하는 사각형 $AODC$의 넓이 $f(\theta)$는
$$f(\theta)=6+\frac{25}{4}\sin2\theta-\frac{9}{2}\sin^2\theta$$가 된다. 특히, $\theta=\pi/4$이면 사각형 $AODC$의 넓이는 $10$이 된다.
$f(\theta)$를 미분하면, \begin{split}f^{\prime}(\theta)&=\frac{25}{2}\cos2\theta-9\sin\theta\cdot \cos\theta \\&= \frac{25}{2}\cos2\theta-\frac{9}{2}\sin 2\theta \end{split}
이고, $0\leq \theta\leq \pi/4$이므로 $f(\theta)$는 $f^{\prime}(\theta)=0$에서
$\displaystyle{\tan2\theta=\frac{25}{9},\;\;\sin2\theta=\frac{25}{\sqrt{706}}}$, 그리고 $\displaystyle{\cos2\theta=\frac{9}{\sqrt{706}}}$일 때 최댓값을 가진다.
(참고: 이때, $\displaystyle{f(\theta)=\frac{15+\sqrt{706}}{4}>10}$이다.)
따라서 삼각형 $AOB$의 넓이는 $\displaystyle{8\sin\theta\cos\theta=4\sin2\theta=\frac{100}{\sqrt{706}}}$이다.