2023학년도 서울대학교 면접 수학 문제
중학교로 오고 나서 대입 문제를 푸는 일에는 게으르다. 일단 서울대학교 일반전형 문제를 올려둔다. 언제나 서울대학교 수학 문제는 어려운데 대입에서 손 놓고 중학교 문제만 풀면서 3년째인 지금도 풀 수 있을까 궁금하다.
문제
함수 $f(x)$와 그 그래프는 아래와 같다.
$$f(x)=\begin{cases}0&(x<0)\\2x&\left(0\leq x<\frac{1}{2}\right)\\2-2x&\left(\frac{1}{2}\leq x<1\right)\\0&(1\leq x)\end{cases}$$

실수 $a$에 대하여 함수 $g(x)$를
$$g(x)=af(x)$$라고 하자.
.
$a=1$일 때 합성함수 $g(g(g(x)))$가 미분가능하지 않은 점의 개수를 구하시오.
.
다음 네 가지의 경우 각각에 대하여
$$0\leq a,\;\;0<a\leq \frac{1}{2},\;\;\frac{1}{2}<a < 1 ,\;\; 1<a$$ 함수 $y=g(g(g(x)))$의 그래프의 개형을 그리시오.
또한, 모든 미분가능 하지 않은 점에서의 함숫값이 (i) $0$보다 크거나 작거나 같은지, (ii) $a$보다 크거나 작거나 같은지 설명하시오. (미분가능하지 않은 점의 좌표를 서술할 필요 없음.)
.
다음 등식이 성립하도록 하는 실수 $a$의 값을 모두 구하시오.
$$\int_{0}^{1}g(g(x))dx=\int_{0}^{1}g(x)dx$$
풀이
1-1. 구간에 따라 정해지는 함수이므로 경계가 되는 점만 생각하면 쉽게 합성함수의 그래프를 그릴 수 있다.
$a=1$이면 $g=f$이다.
먼저 $y=f(f(x))$의 그래프는 아래와 같다.

따라서 $y=f(f(f(x)))$의 그래프는 아래와 같으므로 미분가능하지 않은 점의 개수는 $9$개이다.

1-2. 각각의 경우 함수 $g(x)$의 그래프를 먼저 그려보자.
$\displaystyle{g\left(\frac{1}{2}\right)=a}$이므로 각각의 그래프는 아래와 같다.

합성함수의 그래프는 $y=g(x)$와 $y=1/2$와 $y=1$이 만나는 점을 추적하여 그리면 된다.
1) $1<a$일 때,


미분불가능한 점에서 함숫값은 $0$ 또는 $a$와 같음을 확인할 수 있다.
2) $\displaystyle{\frac{1}{2}<a<1}$일 때,

미분불가능한 점에서의 함숫값은 $a$와 같은 것과 작은 것이 있다. 물론 $0$인 것도 있다.
3) $\displaystyle{0<a<\frac{1}{2}}$일 때,
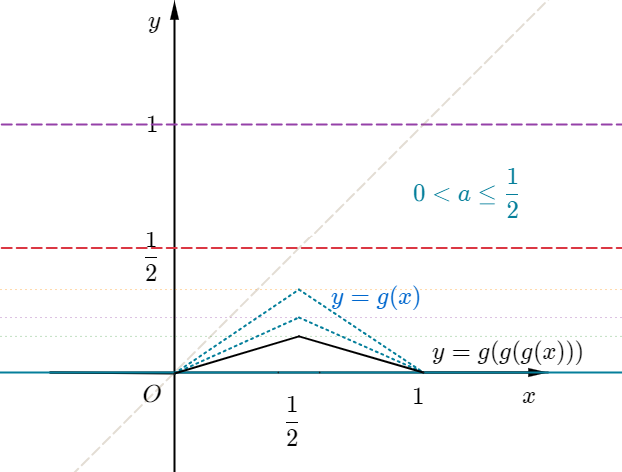
미분불가능한 점에서의 함숫값은 $a$보다 작다.
4) $a\leq0$일 때, $g(g(g(x)))=0$이므로 미분불가능한 점이 없다.
1-3. $a=0$, $a=1/2$, $a=1$일 때, 주어진 등식이 성립한다.
$\blacksquare$
문제
10원짜리, 100원짜리, 500원짜리 동전이 각각 하나씩 놓여있다.
차례로 동전을 한 개씩 뒤집는 작업을 통해 동전을 다음의 상태로 바꾸려고 한다.
(*) 3개의 동전이 모두 앞면이거나 모두 뒷면
동전을 뒤집을 순서를 차례대로 나열한 수열을 ‘뒤집기 수열’이라고 하자.
즉, ‘뒤집기 수열’ $\{a_n\}$은 $n$번째에 $a_n$원짜리 동전을 뒤집는 것을 말하며 수열 $\{a_n\}$의 모든 항은 $10, \;100,\; 500$ 중 하나이다. 예를 들어, ‘뒤집기 수열’ $100,\;500,\;\cdots$에 따라 동전을 뒤집으면 다음과 같다.

도전자가 ‘뒤집기 수열’을 하나 제시하면, 심판이 3개의 동전을 (*) 상태가 아니도록 무작위로 놓은 후, 도전자가 제시한 ‘뒤집기 수열’에 따라 동전을 뒤집는다. 3개의 동전이 (*) 상태가 되면 뒤집기를 멈춘다.
.
모든 ‘뒤집기 수열’에 대해 $1$번 만에 3개의 동전이 (*) 상태로 바뀔 확률은 같다. 그 확률을 구하시오.
.
$2$번 이내에 3개의 동전이 (*) 상태로 바뀔 확률을 최대로 만드는 ‘뒤집기 수열’ 하나의 처음 두 개 항을 제시하고 그 최대의 확률을 구하시오.
.
$n$번 이내에 3개의 동전이 (*) 상태로 바뀔 확률이 1인 ‘뒤집기 수열’이 존재하도록 하는 $n$의 최솟값을 구하시오.
.
위에서 (*) 상태를 아래의 (**) 상태로 대체한다.
(**) 3개의 동전이 모두 앞면
도전자가 ‘뒤집기 수열’을 하나 제시하면, 심판이 3개의 동전을 (**) 상태가 아니도록 무작위로 놓은 후, 도전자가 제시한 ‘뒤집기 수열’에 따라 동전을 뒤집는다. 3개의 동전이 (**) 상태가 되면 뒤집기를 멈춘다.
$n$번 이내에 3개의 동전이 (**) 상태로 바뀔 확률이 1인 ‘뒤집기 수열’이 존재하도록 하는 $n$의 최솟값을 구하시오.
풀이
2-1 복잡한 확률문제를 풀 때는 먼저 표본공간을 명확하게 파악하는 것이 중요하다. 동전이 3개이므로 모두 8가지 경우가 있지만 모두 앞면이거나 뒷면인 경우를 빼면 6가지 경우가 있다. 따라서 표본공간은 아래와 같다. 쉽게 나타내기 위해 차례는 10원, 100원, 500원짜리로 정하고 앞면은 0, 뒷면은 1로 나타내자.
$$S=\{001,010,100,011,101,110\}$$
1번 만에 (*)인 상태가 되는 확률은 쉽게 확인할 수 있다. 항이 하나인 뒤집기 수열은 모두 세 가지가 있다. 뒤집기 수열이 $a_1=10$이면 100은 000으로 011은 111로 바뀌며 게임이 끝난다. 따라서 확률은
$$\frac{2}{6}=\frac{1}{3}$$
문제에 이미 모든 뒤집기 수열이 같은 확률이라고 했으므로 확인할 필요도 없다.
$a_1=100$이면 010은 000으로 101은 111로 바뀌고 $a_1=500$이면 001은 000으로 110은 111로 바뀐다.
1-2
2번이내에 (*)인 상태가 될 확률을 생각하자.
항이 둘인 뒤집기 수열은 두 가지 경우로 분류할 수 있다. $a_1=a_2$과 $a_1\not=a_2$이다. $a_1\not=a_2$이 확률이 더 크다는 것을 알 수 있다.
뒤집기 수열 $10,100,\cdots$일 때를 표로 나타내면 아래와 같다.
| 경우 | 표본공간 | 1번째 뒤집기 | 2번째 뒤집기 |
| 1 | 001 | 101 | 111 |
| 2 | 010 | 110 | 100 |
| 3 | 100 | 000 | x |
| 4 | 011 | 111 | x |
| 5 | 101 | 001 | 011 |
| 6 | 110 | 010 | 000 |
뒤집을 때마다 각각의 자리에 있는 0과 1의 개수는 서로 같다. 따라서 $a_1\not=a_2$인 모든 수열은 확률이 같다.
1-3.
이제 남아 있는 2번과 5번일 때 10원짜리 동전을 뒤집으면 3번 이내에 (*)가 될 확률이 1이 되는 뒤집기 수열을 만들 수 있다. 따라서 뒤집기 수열 $10,100,10,\cdots$이면 모든 경우 게임이 끝나게 되므로 구하는 최솟값은 3이다.
1-4.
표본공간이 아래와 같이 달라진다.
$$S=\{001,010,100,011,101,110,111\}$$
마찬가지로 표를 그려 보자. 최솟값을 구하는 전략은 1이 하나만 있는 경우를 000으로 바꾸는 것이다. 뒤집기 수열 $10,100,10,500,10,\cdots$일 때는 아래와 같다.
| 경우 | 표본공간 | 1번째 뒤집기 | 2번째 뒤집기 | 3번째 뒤집기 | 4번째 뒤집기 | 5번째 뒤집기 |
| 1 | 001 | 101 | 111 | 011 | 010 | 110 |
| 2 | 010 | 110 | 100 | 000 | x | |
| 3 | 100 | 000 | x | |||
| 4 | 011 | 111 | 101 | 001 | 000 | x |
| 5 | 101 | 001 | 011 | 111 | 110 | 010 |
| 6 | 110 | 010 | 000 | x | ||
| 7 | 111 | 011 | 001 | 101 | 100 | 000 |
확률이 1이 되는 뒤집기 수열이 존재하는 최솟값은 7이다.
$\blacksquare$
문제
포물선 $C_1$의 방정식은 $y=-x^2+1$이고, 점$P_1$의 좌표는 $(1,0)$이다. 직선 $l$은 포물선 $C_1$ 위의 점 $(c,-c^2+1)$에서의 접선이다. (단, $c$는 $\displaystyle{\frac{1}{2}<c<1}$인 고정된 실수이다.) 포물선 $C_2$는 $C_1$을 평행이동한 포물선이고 직선 $l$과 접하며 $P_1$을 지난다. (단, $C_1$와 $C_2$은 서로 다르다.) 점 $P_2(q_2,0)$은 $C_2$와 $x$축과의 교점이다. (단, $P_1$와 $P_2$은 서로 다르다.)

.
포물선 $C_2$의 꼭짓점의 $x,y$ 좌표를 각각 $c$에 대한 식으로 나타내시오.
.
직선 $x=q_2$와 직선 $l$ 및 포물선 $C_2$로 둘러싸인 도형의 넓이를 $c$에 대한 식으로 나타내시오.
.
위와 같이 모든 자연수 $k$에 대하여 포물선 $C_k$와 $C_k$ 위의 점 $P_k(q_k,0)$이 주어져 있을 때, 포물선 $C_{k+1}$ 위의 점 $P_{k+1}(q_{k+1},0)$이 다음과 같이 주어진다.
(1) 포물선 $C_{k+1}$은 $C_1$을 $x$축의 방향으로 $a_{k+1}$만큼, $y$축의 방향으로 $b_{k+1}$만큼 평행이동한 포물선이고 직선 $l$과 접하며 $P_k$를 지난다. (단, $C_{k+1}$과 $C_{k}$는 서로 다르다.)
(2) 점 $P_{k+1}$은 $C_{k+1}$과 $x$축과의 교점이다. (단, $P_{k+1}$과 $P_{k}$는 서로 다르다.)
$a_{k+1}$을 $a_{k}\;,q_k\;,c$에 대한 식으로 나타내고, (필요하다면 이를 이용하여)
$q_{k+1}$을 $a_{k},\;q_k,\;c$에 대한 식으로 나타내시오. (단, $a_1=b_1=1$, $q_1=1$)
풀이
3-1.
직선 $l$은 기울기가 $-2c$이고 점 $(c,-c^2+1)$을 지나므로 방정식은 아래와 같다.
$$y=-2c(x-c)-c^2+1$$
$$y=-2cx+c^2+1\tag{1}$$
포물선 $C_2$의 방정식은 $$y=-(x-1)(x-q_2)\tag{2}$$이다.
(1)과 (2)에서
$$-2cx+c^2+1=-(x-1)(x-q_2)$$
$$x^2-(q_2 +2c+1)x+c^2+q_2 +1=0$$
직선 $l$과 포물선이 서로 접하므로
$$D=(q_2+2c+1)^2-4(c^2+q_2 +1)=0$$
$$q_2^2-2(1-2c)q_2 +4c-3=0$$
$$(q_2+1)(q_2+4c-3)=0$$
$q_2=-1$ 또는 $q_2=-4c+3$이다.
$q_2=-1$이면 두 포물선 $C_1$과 $C_2$가 일치한다. 따라서 $q_2=-4c+3$이다.
(2)의 꼭짓점의 $x$좌표는
$$\frac{1+q_2}{2}=\frac{-4c+4}{2}=-2c+2$$
이고 $y$좌표는
$$-(-2c+2-1)(-2c+2+4c-3)=(2c-1)^2$$
3-2.
구하는 영역의 넓이를 $A$라고 하자. 접점의 $x$좌표는 $-c+2$이다.
\begin{split}A&=\int_{q_2}^{-c+2}[(-2cx+c^2+1)-(-(x-1)(x-q_2))]dx\\&=\int_{q_2}^{-c+2}[x^2-(q_2 +2c+1)x+c^2+q_2 +1] dx\end{split}
$q_2=-4c+3$을 대입하여 계산하면
\begin{split}A&=\int_{-4c+3}^{-c+2}[x^2+2(c-2)x+(c-2)^2]dx\\&=\int_{-4c+3}^{-c+2}(x+c-2)^2dx\\&=\frac{1}{3}(x+c-2)^3]_{-4c+3}^{-c+2}\\&=\frac{1}{3}(3c-1)^3\end{split}
3-3.
포물선 $C_{k+1}$의 방정식은
$$y=-(x-a_{k+1})^2+1+b_{k+1}=-x^2+2a_{k+1}x-a_{k+1}^2+b_{k+1}+1$$
포물선 $C_{k+1}$과 직선 $l$이 접하므로
$$-x^2+2a_{k+1}x-a_{k+1}^2+b_{k+1}+1=-2cx+c^2+1$$
정리하면
$$x^2-2(a_{k+1}+c)x+a_{k+1}^2-b_{k+1}+c^2=0$$
$$\frac{D}{4}=(a_{k+1}+c)^2-a_{k+1}^2+b_{k+1}-c^2=2ca_{k+1}+b_{k+1}=0$$
에서 $$b_{k+1}=-2ca_{k+1}\tag{3}$$
마찬가지로 $$b_{k}=-2ca_{k}\tag{4}$$
이다.
또한, 포물선 $C_{k+1}$의 방정식은 $x$축과의 교점이 $(q_k,0),\;(q_{k+1},0)$이므로 아래 이차방정식의 두 근은 $q_k, q_{k+1}$이다.
$$-x^2+2a_{k+1}x-a_{k+1}^2+b_{k+1}+1=0$$
(3)을 대입하여 정리하면
$$x^2-2a_{k+1}x+a_{k+1}^2+2ca_{k+1}-1=0\tag{5}$$
두 근은 $q_k, q_{k+1}$이다.
마찬가지로 $C_k$의 방정식은 $x$축과의 교점이 $(q_{k-1},0),\;(q_{k},0)$이므로 아래 이차방정식의 두 근은 $q_{k-1}, q_{k}$이다.
$$-x^2+2a_{k}x-a_{k}^2+b_{k}+1=0$$
정리하면
$$x^2-2a_{k}x+a_{k}^2+2ca_{k}-1=0\tag{6}$$이다.
(5)와 (6)은 공통근 $q_k$를 갖는다.
(5)-(6)에서
$$-2(a_{k+1}-a_k)q_k+(a_{k+1}-a_k)(a_{k+1}+a_k)+2c(a_{k+1}-a_k)=0$$
$$(a_{k+1}-a_k)(-2q_k+a_{k+1}+a_k+2c)=0$$이다. $P_{k+1}$과 $P_k$가 다르므로 $a_{k+1}\not=a_k$이다.
따라서 $$-2q_k+a_{k+1}+a_k+2c=0$$이다.
$$a_{k+1}=-a_k+2q_k-2c$$
$\displaystyle{a_{k+1}=\frac{q_{k+1}+a_k}{2}}$이므로 $$q_{k+1}=-q_k+2a_{k+1}=-q_k+2(-a_k+2q_k-2c)=3q_k-2a_k-4c$$
$\blacksquare$
