삼각비 한 발자국 더!
중학교 수학을 가르칠 때 과연 이것이 중학교 과정인가 아닌가 헷갈릴 때가 있다.
세 변의 길이를 아는 삼각형에서 삼각비 구하기
삼각비 문제를 하나 만들어 보자. 중학교 교과서는 보통 삼각비를 직각삼각형에서 정의한다.
세 변의 길이가 각각 $3, 4, 6$인 삼각형은 하나로 결정된다. 당연히 세 각의 크기도 결정된다. 그러면 아래와 같은 삼각형에서 $\cos A$의 값을 구할 수 있다. 이것은 중학교 문제인가? 고등학교 문제인가?

삼각비의 뜻에 따라 $\cos A$의 값을 구하기 위해서는 각 $A$를 포함한 직각삼각형이 있어야 한다. 점 $C$에서 변 $AB$에 내린 수선의 발을 $D$라 하고 $\overline{AD}=x$라고 하자.

간단하게 $x$의 값을 구할 수 있다. 피타고라스 정리에 따라
$$\overline{DC}^2=4^2 -x^2=3^3-(6-x)^2\tag{1}$$
$$x=\frac{43}{12}$$
따라서
$$\cos A=\frac{43}{12}\div 4=\frac{43}{12}\times \frac{1}{4}=\frac{43}{48}$$
번분수 표현이 필요하니까 중학교 과정을 벗어난다고 봐야 할까? 하지만 위와 같이 번분수 없이도 계산은 어렵지 않다.
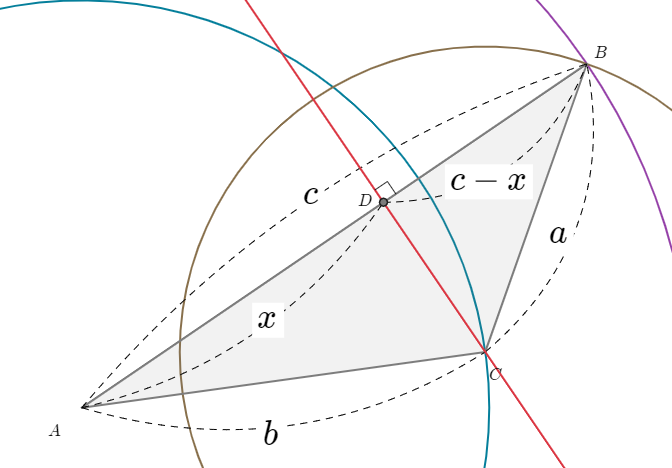
위에서 했던 일을 문자로 다시 써보자.
$$\overline{DC}^2=b^2 -x^2=a^3-(c-x)^2\tag{3}$$
$$b^2 -x^2=a^3-c^2+2cx-x^2$$
$$b^2+c^2 -a^2 =2cx$$
$$x=\frac{b^2+c^2-a^2}{2c}$$
$$\cos A=\frac{x}{b}=\frac{b^2+c^2-a^2}{2bc}$$
$$\cos A=\frac{b^2+c^2-a^2}{2bc}\tag{4}$$
(3)을 사용하면 바로 구할 수 있다. 이것이 바로 코사인 제2법칙이다. 이걸 외워서 해결한다면 모르겠지만 (1)처럼 구하는 풀이는 중학교 과정을 벗아난다고 할 수 없다. 이제는 고등학교 과정에도 코사인 법칙이 나오지 않는다. 말이 나온 김에 코사인 제2법칙을 증명해 보자. 코사인 제2법칙은 피타고라스 정리의 일반화라고 할 수 있다.
이처럼 교육과정의 경계가 모호할 때 선행학습 금지법 때문에 망설이게 된다.
코사인 법칙
원의 성질로 증명

$$\overline{BA}\times \overline{AF}=\overline{EA}\times \overline{AG}$$
$$c(2a\cos B-c)=(a-b)(a+b)$$
$$c^2 =a^2 +b^2 -2ab\cos \theta$$
Timothy A. Sipka의 증명

$$\overline{CD}=b\cos C$$
$$\overline{AD}=b\sin C$$
$$\overline{BD}=a-b\cos C$$
피타고라스 정리에 따라
$$\overline{BD}^2+\overline{BD}^2=\overline{AB}^2$$
$$(a-b\cos C)^2+(b\sin C)^2=c^2$$
$$a^2-2ab\cos C+b^2 \cos^2 C+b^2 \sin^2 C=c^2$$
$$a^2-2ab\cos C+b^2 =c^2$$
톨레미 정리로 증명
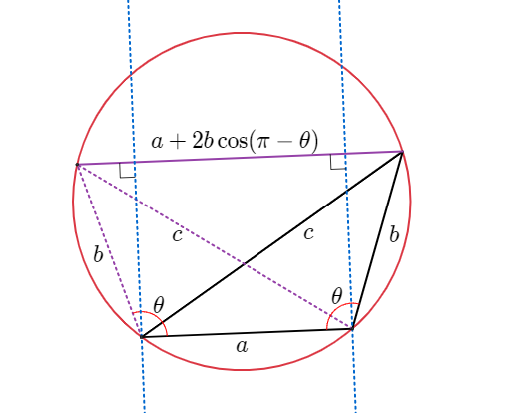
$$c\cdot c=b\cdot b+(a+2b\cos(\pi-\theta))\cdot a$$
$$c^2 =a^2 +b^2 -2ab\cos \theta$$