2024학년도 수시 서울대학교 면접 문제_01
바쁜 업무를 모두 끝내고 심심해서 대학 입시 문제를 풀었다. 오늘은 서울대 면접 문제다. 생각보다 잘 풀려서 기분이 좋다. 내년엔 다시 고등학교로 돌아가서 미적분 문제도 풀고 싶으니 그때를 위해 가끔씩 풀고자 한다.
문제
곡선 $C$의 방정식은 $\displaystyle{y=x^2 +\frac{5}{4}}$이다. 다음 그림과 같이 점 $A(a,b)$에서 곡선 $C$에 서로 다른 두 접선을 그을 수 있을 때, 그 두 접선과 곡선 $C$의 접점을 각각 $\displaystyle{P\bigg(p,\;p^2 +\frac{5}{4}\bigg)}$, $\displaystyle{Q\bigg(q,\;q^2 +\frac{5}{4}\bigg)}$라고 하자. (단, $p<q$)
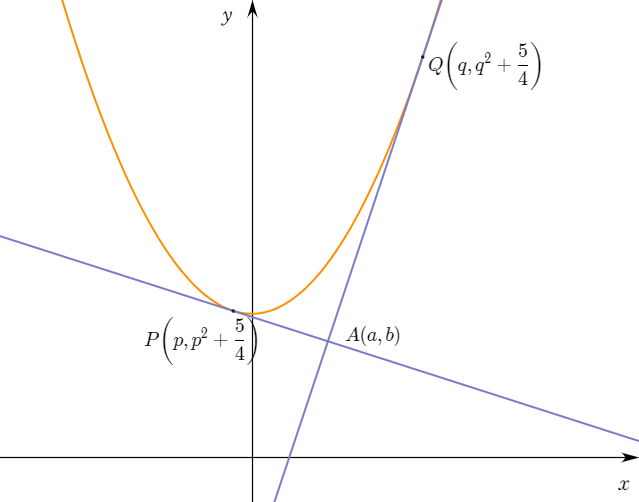
1-1. $\displaystyle{\frac{\overline{AP}^2+\overline{AQ}^2}{\overline{PQ}^2}}$의 값을 $p$와 $q$에 대한 식으로 나타내어라.
1-2. 점 $A$가 곡선 $C$와 만나지 않는 직선 $\displaystyle{y=\frac{3}{2}x}$ 위에 있을 때, $\displaystyle{\frac{\overline{AP}^2+\overline{AQ}^2}{\overline{PQ}^2}}$의 값을 점 $A$의 $x$ 좌표 $a$에 대한 식으로 나타내시오.
1-3. 실수 $a$에 대하여 문제 1-2에서 얻은 식을 $f(a)$라고 하자.
(1) 함수 $y=f(x)$의 최댓값 $M$과 최솟값 $m$을 구하시오.
(2) 방정식 $f(x)=t$의 실근의 개수가 하나가 되도록 하는 실수 $t$ (단, $m<t<M$)는 하나뿐임을 보이고, 그때의 $t$의 값을 구하시오.
1-4. 곡선 $C$를 $y$축 방향으로 $\displaystyle{-\frac{1}{4}}$만큼 평행이동한 곡선을 $C_1$이라고 하자. 직선 $\displaystyle{y=\frac{3}{2}x}$ 위의 점 $A$의 $x$좌표 $a$가 문제 1-2-3에서 구한 $t$에 대하여 $f(a)=t$를 만족할 때, 선분 $AP$, 선분 $AQ$, 곡선 $C_1$으로 둘러싸인 도형의 넓이를 구하시오.
1-1. 먼저 점 $A$의 좌표를 $p$와 $q$로 나타내야 한다. 이를 위해 두 접선인 직선 $AP$와 직선 $AQ$의 방정식을 구하면 아래와 같다.
$$y=2px-p^2+\frac{5}{4}\tag{1}$$
$$y=2qx-q^2+\frac{5}{4}\tag{2}$$
(1)과 (2)의 교점이 $A(a,b)$이다.
$$a=\frac{p+q}{2}, \;\;b=pq+\frac{5}{4}\tag{3}$$
$$\begin{split}\overline{AP}^2&=\bigg(p-\frac{p+q}{2}\bigg)^2+\bigg(p^2+\frac{5}{4}-pq-\frac{5}{4}\bigg)^2\\&=\bigg(\frac{p-q}{2}\bigg)^2+(p^2-pq)^2\\&=(p-q)^2\bigg(\frac{1}{4}+p^2\bigg)\\\overline{AQ}^2&=(p-q)^2\bigg(\frac{1}{4}+q^2\bigg)\\\overline{PQ}^2&=(p-q)^2+(p^2 -q^2)^2\\&=(p-q)^2(1+(p+q)^2)\end{split}$$
$$\displaystyle{\frac{\overline{AP}^2+\overline{AQ}^2}{\overline{PQ}^2}}=\cfrac{\cfrac{1}{2}+p^2+q^2}{1+(p+q)^2}=\cfrac{(p+q)^2 -2pq+\cfrac{1}{2}}{1+(p+q)^2}\tag{4}$$
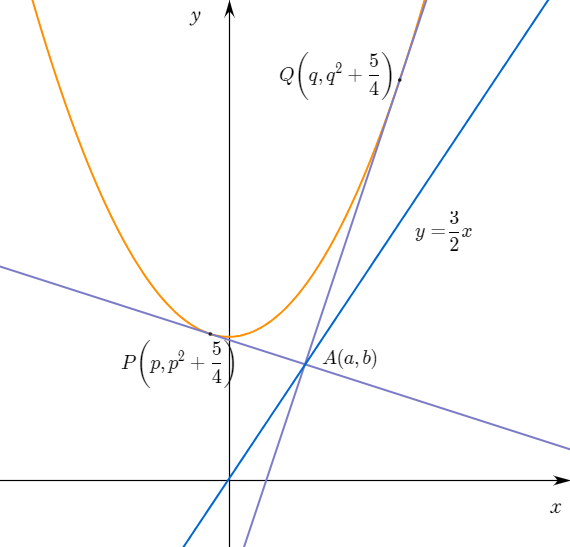
1-2. 점 $A(a,b)$가 직선 $\displaystyle{y=\frac{3}{2}x}$위에 있으므로 $\displaystyle{b=\frac{3}{2}a}$이다.
(3)을 다시 정리하면 $$p+q=2a\;\;pq=b-\frac{5}{4}=\frac{3}{2}a-\frac{5}{4}$$이다. (4)에 대입하여 정리하면
$$\displaystyle{\frac{\overline{AP}^2+\overline{AQ}^2}{\overline{PQ}^2}}=\frac{4a^2-3a+3}{1+4a^2}=1+\frac{2-3a}{1+4a^2}$$
1-3. (1)$$f(x)=1+\frac{2-3x}{1+4x^2}$$
$$\begin{split} f^{\prime}(x)&=\frac{-3(1+4x^2)-8x(2-3x)}{(1+4x^2)^2}\\&=\frac{12x^2-16x-3}{(1+4x^2)^2}\\&=\frac{(6x+1)(2x-3)}{(1+4x^2)^2}\end{split}$$
증감을 조사하면 $\displaystyle{x=-\frac{1}{6}, \;\;x=\frac{3}{2}}$에서 극값을 가진다. 그래프를 그리면 아래와 같다. 점근선은 $y=1$이다.
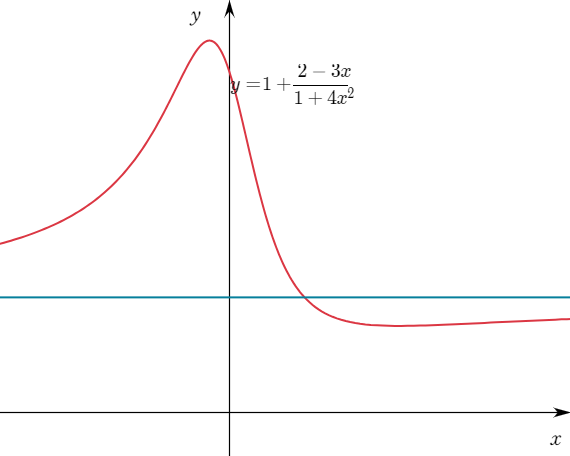
극값이 최댓값과 최솟값이 된다.
$$M=f\bigg(-\frac{1}{6}\bigg)=\frac{13}{4},\;\;m=f\bigg(\frac{3}{2}\bigg)=\frac{3}{4}$$
(2) 점근선은 $y=1$이므로 방정식 $f(x)=t$의 실근의 개수가 하나가 되도록 하는 실수 $t=1$이다.
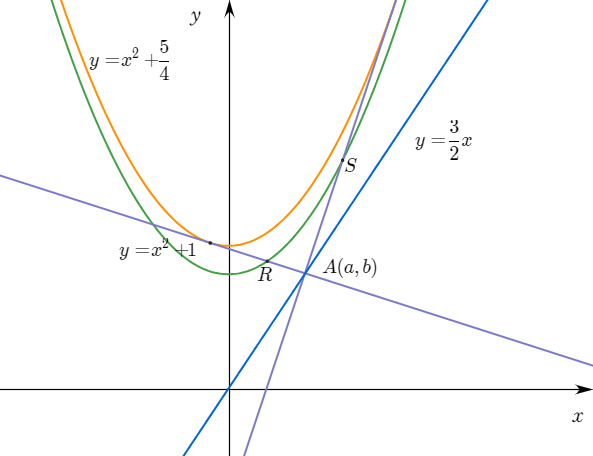
1-4 마지막은 정적분으로 구하면 되는데 계산이 복잡하다.
먼저 $f(a)=1$에서 $a=2/3$이다. 따라서 $$A\bigg(\frac{2}{3},1\bigg)$$이다.
$$\frac{p+q}{2}=\frac{2}{3},\;\;pq=-\frac{1}{4}$$
정리하면 $\displaystyle{p=-\frac{1}{6},\;\;q=\frac{3}{2}}$이므로 두 접선의 방정식은 아래와 같다.
$$\overline{AP}:\;\;y=-\frac{1}{3}x+\frac{44}{36},\quad\;\;\overline{AQ}: \;\;y=3x-1$$
$C_1$과 만나는 점 $R$과 $S$을 구하자. $\displaystyle{R\bigg(\frac{1}{3},\frac{10}{9}\bigg),\;\;S(1,2)}$이다.
정적분으로 곡선 $C_1$과 $x$축 사이 넓이를 구하고 사다리꼴 넓이를 빼기로 하자.
$$\int_{1/3}^{1}(x^2+1 )dx=\bigg[\frac{1}{3}x^3+x\bigg]_{1/3}^{1}=\frac{80}{81}$$
$$\frac{1}{2}\bigg(\frac{10}{9}+1\bigg)\times\frac{1}{3}+\frac{1}{2}(1+2)\times\frac{1}{3}=\frac{23}{27}$$
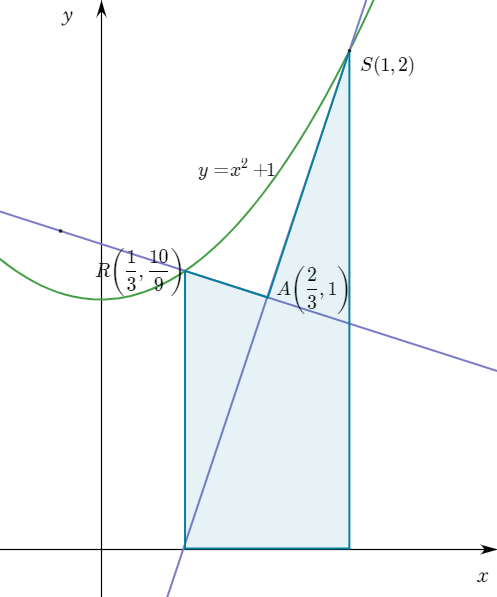
아 마지막까지 계산이 지저분하다.
정답은 $\displaystyle{\frac{11}{81}}$이다.
문제
양의 정수 $n(n\geq 2)$에 대하여 수직선 위의 $n$개의 점 $P_1.P_2,\cdots P_n$이 다음 [규칙]에 따라 움직이고 있다.
[규칙]
(가) 점 $P_k$는 수직선 위의 점 $-k$에서 출발하여 속도 $v_k$로 움직인다. 즉, 시각 $t$에서 점 $P_k$의 위치는 $-k+v_k t$로 이다.
(나) 모든 점들은 동시에 출발하며, 점들의 속도는 다음을 만족한다.$$0<v_1 <\cdots<v_k$$
(다) 두 개 이상의 점이 한 곳에서 만나면 그 점들은 모두 사라진다. (단, 점들이 동시에 같은 위치에 놓이면 "만난다"라고 한다.)
예를 들어 $n=3$인 경우, 3개의 점들이 움직이는 속도가 $v_1 =1,\;\; v_2=3, \;\;v_3=4$로 주어지면, 시각 $t=1/2$에서 두 점 $P_1$과 $P_2$가 수직선 위의 점 $-1/2$에서 만나서 사라진다. 점 $P_3$은 다른 점과 만나서 사라지지 않고 계속 움직인다.


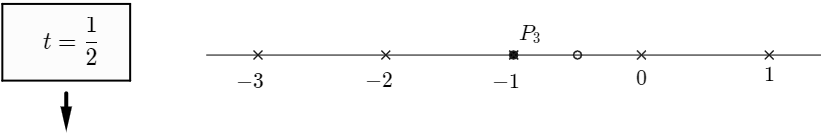
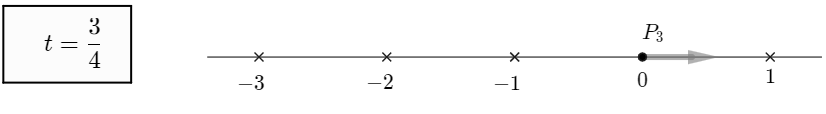
2-1 $n=5$인 경우, 5개의 점들이 움직이는 속도가 다음과 같이 주어져 있다.
| $$v_1$$ | $$v_2$$ | $$v_3$$ | $$v_4$$ | $$v_5$$ |
| 1 | 4 | 6 | 18 | 20 |
사라지지 않고 계속 움직이는 점을 구하시오.
2-2 $n=7$인 경우, 7개의 점들이 움직이는 속도가 다음과 같이 주어져 있다.
| $$v_1$$ | $$v_2$$ | $$v_3$$ | $$v_4$$ | $$v_5$$ | $$v_6$$ | $$v_7$$ |
| $a$ | 4 | 7 | 8 | $b$ | 15 | 25 |
사라지지 않고 계속 움직이는 점이 $P_1$이 되도록 하는 순서쌍 $(a,b)$를 모두 구하시오. (단, $a,\;\;b$는 양의 정수)
2-3. $n=100$인 경우, 100개의 점들이 움직이는 속도가 다음과 같이 주어져 있다.
$$v_k=\cases{k^2+d \quad\quad (1\leq k\leq 50)\\ k^2+d+9 \quad (51\leq k \leq 100)}$$
시각 $\displaystyle{t=\frac{1}{106}}$사라지지 않고 남아 있는 점의 개수를 구하시오. (단, $d$는 양의 정수이다.)
2-4 문제 2-3의 상황에서, 100개의 점 중 원점을 통과한 뒤 사라지는 점의 개수가 50이 되도록 하는 양의 정수 $d$의 개수를 구하시오. (단, 어떤 점이 원점에서 다른 점과 만나서 사라졌다면, 이 점은 원점을 통과하지 못한 것으로 한다.)
풀이
수직선 위에서 움직이는 운동이므로 아래와 같은 1차 함수로 생각할 수 있다.
$$P_k (x)=-k+v_k x$$
예제에 있는 상황을 1차 함수의 그래프로 나타내면 아래와 같다.
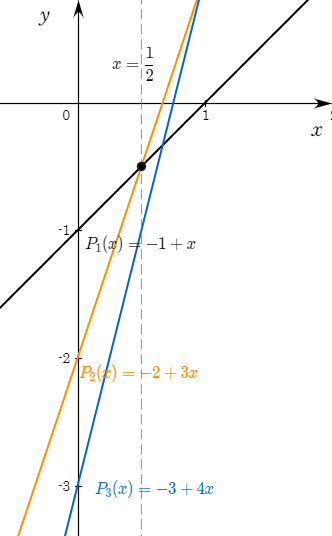
두 점 $P_m, P_n$이 만나는 시각을 대수적으로 표현하면 아래와 같다.
$$-m+v_m t= -n+v_n t$$
$$t=\frac{m-n}{v_m -v_n}$$
속도의 차가 크고 떨어진 거리는 짧은 점들이 먼저 만나서 사라진다.
2-1
먼저 $\displaystyle{t=\frac{4-3}{v_4-v_3}=\frac{1}{12}}$일 때, $P_3, P_4$가 만나서 사라짐을 쉽게 알 수 있다.
다음으로 $\displaystyle{t=\frac{5-2}{v_5-v_2}=\frac{3}{16}}$일 때, $P_2, P_5$가 만나서 사라지지 않고 남는 점은 $P_1$이다.
2-2
먼저 $\displaystyle{t=\frac{7-6}{v_7-v_6}=\frac{1}{10}}$일 때, $P_6, P_7$가 만나서 사라짐을 쉽게 알 수 있다.
다음으로 $0<a<4$이고 $8<b<15$이므로 순서쌍을 차근차근 찾으면 된다.
$a=1$일 때,
$b$의 값에 상관없이 $t=1/3$에서 $P_1,P_2, P_3$가 동시에 사라진다.
$a=2$일 때,
$b=9,10$이라면 $t=1/3$에서 $P_2, P_3$가 사라진 다음 $P_1, P_4$가 사라진다.
따라서 $b=11,12,13,14$이다.
$a=3$일 때,
$b=9$이라면 $t=1/3$에서 $P_2, P_3$가 사라진 다음 $P_1, P_4$가 사라진다.
따라서 $b=10,11,12,13,14$이다.
하나하나 적으려니 너무 귀찮다.
2-3
$k=m$과 $k=m+1$인 점이 만나는 시각을 구해보자.
$m\not=50$일 때, $\displaystyle{t=\frac{(m+1)-m}{(m+1)^2-m^2}=\frac{1}{2m+1}}$
$m=50$일 때, $\displaystyle{t=\frac{51-50}{(51^2+d+9)^2-(50^2+d)}=\frac{1}{101+9}=\frac{1}{110}}$
$\displaystyle{\frac{1}{199}}$일 때, $P_{99}$과 $P_{100}$이 만나서 사라진다.
$\vdots$
$\displaystyle{\frac{1}{107}}$일 때, $P_{53}$과 $P_{54}$가 만나서 사라진다.
한편, 중간에 $\displaystyle{\frac{1}{110}}$일 때, $P_{50}$과 $P_{51}$이 만나서 사라진다.
따라서 $\displaystyle{\frac{1}{106}}$일 때, 사라지지 않고 남아 있는 점은 $P_1, P_2, \cdots P_{49}, P_{52}$로 모두 50개이다.
2-4
점이 짝을 이루어 사라지므로 25번째로 사라지는 두 점은 음수인 위치에서 만나고 26번째 사라지는 두 점은 양수인 위치에서 만난다고 생각하면 된다.
25번째로 $P_{53},P_{54}$가 사라지는 시각은 $\displaystyle{\frac{1}{107}}$이다.
$\displaystyle{\frac{1}{107}}$일 때, $P_{53}$의 위치는
$$-53+\frac{53^2+d+9}{107}\leq 0\tag{1}$$
26번째로 $P_{49},P_{52}$가 사라지는 시각은
$$\frac{3}{52^2+d+9-(49^2+d)}=\frac{3}{101\times 3+9}=\frac{1}{104}$$
$\displaystyle{\frac{1}{104}}$일 때, $P_{49}$의 위치는
$$-49+\frac{49^2+d}{104}\geq 0\tag{2}$$
(1), (2)에서
$$2695<d\leq 2853$$
정답은 $2853-2695=158$이다.