피타고라스 정리로 푸는 기하 문제_영재학교 입시
중학교에서 벌써 4년째 접어들었다. 영재학교 신입생 선발을 위한 평가 문제를 풀었다. 늘 고등학교 문제만 푸느라 이제까지 영재학교 문제를 풀 기회가 없었다. 요즘 평범한 학생은 교과서 수준만으로도 충분하다. 그러나 사람의 욕심은 끝이 없는 법 영재고나 과학고를 다니고 싶다면 뭔가 깊이 있는 문제를 풀어 봐야 한다. 이런 문제를 해결하려면 학원의 도움을 얻어야 된다고 생각할 것이다. 하지만 누가 돕는다고 영재성이 쉽게 길러지지 않는다. 평범한 중학생에게 이런 문제를 풀게 하고 싶다. 사실 피타고라스 정리만 하더라도 단순하게 외워서 적용하는 문제만 풀면 창의성은 길러지지 않는다. 심화 문제를 풀어야 하는 까닭이다.
2024학년도 세종과학예술영재학교 신입생 선발 2단계 영재성평가 문제
그림과 같이 길이가 26인 선분 $AB$를 빗변으로 하는 직각삼각형 $ABC$와 선분 $AB$를 지름으로 하는 반원이 평면 위에 있다. 선분 $AC$ 위의 점 $D$를 $\overline{CD}=2\overline{CB}$가 되도록 잡고 호 $AB$ 위의 점 $E$를 $\angle ADE=90^{\circ}$가 되도록 잡는다. $\overline{DA}=\overline{DE}$일 때, 다음 물음에 답하시오. [총 16점]
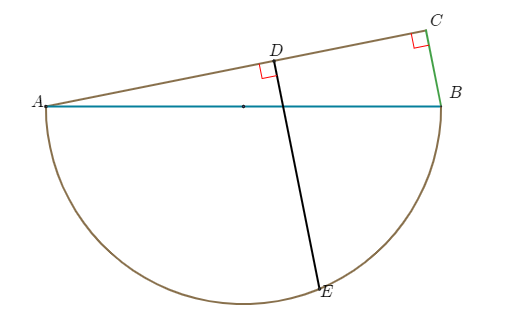
(1) 선분 $BC$의 길이를 구하고 그 과정을 설명하시오. [8점]
(2) 선분 $AB$와 선분 $DE$의 교점을 $N$이라 하고 선분 $AB$ 위에 점 $B$가 아닌 점 $F$를 $\overline{CF}=2\overline{CB}$가 되도록 잡을 때, 선분 $NF$의 길이를 구하고 그 과정을 설명하시오. [8점]
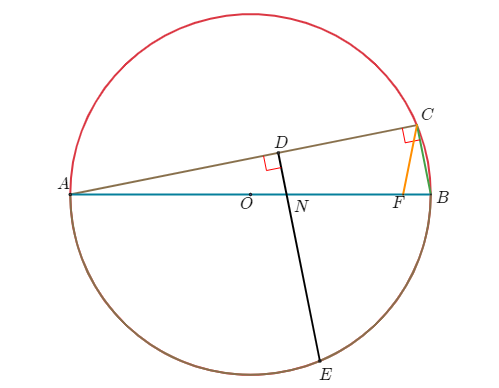
역시 영재학교 문제는 쉽게 접할 수 있는 문제가 아니다. 중학교 교과 수준만으로 풀기 위해 노력하였다. 이런 문제도 피타고라스 정리와 삼각비만 알면 풀 수 있다. 당연히 이론상으론 그렇다이다. 과연 사교육없이 교과서 위주로 공부한 학생이 풀 수 있을까는 의심스럽다.
선분 $AB$를 지름으로 하는 원은 삼각형 $ABC$의 외접원이다. 직각이 많이 등장하고 있으므로 먼저 피타고라스 정리를 떠오른다. 일단 문제 해결에 필요한 미지수를 정해주자.
$\overline{BC}=x$라고 하면 $\overline{CD}=2x$이다. $\overline{AD}=\overline{ED}=y$라고 하고 점 $A$에서 직선 $BC$에 내린 수선의 발을 $F$라 하자. 피타고라스 정리를 쓰자.
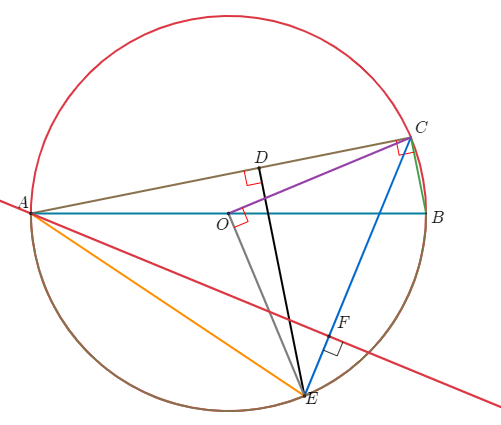
$\triangle DCE $에서 피타고라스 정리를 쓰면
$$\overline{DC}^2+\overline{DE}^2=\overline{EC}^2$$
$$(2x)^2+y^2=(13\sqrt2)^2$$
$$4x^2+y^2=13^2\times2\tag{1}$$
$\overline{AD}=\overline{ED}$이므로 $\angle{DAE}=\angle{DEA}=45^{\circ}$이다.
원주각의 성질에 따라
$$\angle{COD}=2\angle{DAE}=90^{\circ}$$
$$\overline{AE}=y \sqrt{2} ,\;\;\overline{EC}=13\sqrt 2$$
먼저 $\angle{ABC}=\angle{AEC}=\theta $라고 하자.
다음은 삼각비를 쓰자.
$$\cos \theta=\frac{x}{26},\;\;\sin \theta=\frac{2x+y}{26}$$
$\sin^2 \theta+\cos^2 \theta=1$임을 확인해 두자.
$$\overline{EF}=\overline{AE}\cos \theta$$
$$\overline{AF}=\overline{AE}\sin \theta$$
이다. $\triangle AFC$에서 피타고라스 정리를 쓰면
$$\overline{AF}^2+\overline{FC}^2=\overline{AC}^2$$
$$(\overline{AE}\sin \theta)^2+(\overline{EC}-\overline{AE}\cos \theta)^2=\overline{AC}^2$$
$$(y\sqrt2\sin \theta)^2+(13\sqrt2-y\sqrt2 \cos \theta)^2=(2x+y)^2$$
$$2y^2\sin^2 \theta+13^2\times 2 -2\times 13\sqrt2\times y\sqrt2 \cos \theta+2y^2 \cos^2\theta=4x^2+4xy+y^2$$
$$2y^2 +13^2\times 2 -52\times y \times \frac{x}{26}=4x^2+4xy+y^2\quad (\because \sin^2 \theta+\cos^2\theta=1)$$
정리하면
$$4x^2+6xy-y^2=13^2 \times2\tag{2}$$
이다. 이것은 제2코사인법칙으로 구하면 간단하지만 교육과정 밖이라. ㅠㅠ
(1)-(2)에서
$$2y^2-6xy=0$$
$$\therefore y=3x\tag{3}$$
(3)을 다시 (1)에 대입하면 $x=\sqrt {26}$이다.
답을 구하고 보니 빗변의 길이의 제곱근이다. 뭔가 훨씬 간단하게 구하는 방법이 있을 것 같은데 영재가 아니라 쉽게 떠오르지 않는다.
1번을 풀면 2번은 매우 간단하다.
점 $C$에서 선분 $AB$에 내린 수선의 발을 $G$라 하자.
$$\overline{AC}\times\overline{BC}=\overline{AB}\times\overline{CG}$$
$$\overline{CG}=5$$
피타고라스 정리에 따라
$$\overline{BG}^2 +\overline{CG}^2=\overline{BC}^2$$
이므로 간단하게 $\overline{GB}=1$임을 알 수 있다.
닮음비를 이용하면
$$\overline{NB}=\frac{2}{5}\times\overline{AB}=\frac{52}{5}$$
$$\therefore \overline{NF}=\overline{NB}-\overline{FB}=\frac{42}{5}$$