수학이야기
원과 직선으로 세상을 만들다
수학이야기
2024. 10. 8. 09:13
반응형
아래 그림은 국립중앙박물관에 소장된 '복희여와도'이다. 아스타나 고분에서 발굴된 그림이다. 중국 신화에 나오는 복희와 여와가 주인공이다. 오른쪽은 남신이 복희이고 왼쪽 여신이 여와이다. 작은 원들은 해와 달 그리고 별이다. 복희는 직선을 긋는 자(곡척)를 여와는 원을 그리는 컴퍼서(규)를 들고 있는 것이 눈에 띈다면 뭘 좀 아는 사람이다. 중학교 1학년에서 배운 작도가 떠오른다면 많이 아는 사람이다. 그렇다. 중국 사람들은 원과 직선으로 세상을 만들었다고 생각했다. 달리 말하면 원과 직선으로 세상 만물의 이치를 깨우쳤다고 할 수 있다.

규칙의 규가 컴퍼스를 부르는 이름인 것은 아는 사람은 매우 드물다. 법률신문에 나온 글을 옮겨 놓는다.
규칙(規則)은 여러 사람이 다 함께 지키기로 하고 정해 놓은 준칙(準則)이라고 할 수 있습니다. 준칙(準則)은 근거나 기준이 되는 법칙입니다 그러므로 정해 놓은 규칙(規則)을 지키는 것은 당연한 민주 시민의 의무입니다.
이 규칙(規則)은 법 규(規)와 법칙 칙(則)이 합한 말입니다. 규(規)는 부(夫)와 견(見)이 합한 글자입니다. 부(夫)는 지아비라 훈(訓)을 하는 것으로 여기서는 표준보다 나은 사람이라는 뜻이고 그런 사람이 보는(見) 것은 바르고 공평할 것이라 해서 법 규(規)가 나왔습니다.
바르게 보려면 어떤 척도가 있어야 합니다. 이 규(規)가 척도로 쓰인 것입니다. 이는 오늘날의 컴퍼스의 의미로도 쓰입니다. 규구준승(規矩準繩)도 그래서 나온 말입니다. 규(規)는 컴퍼스, 구(矩)는 ㄱ자의 굽은 것을 그리는 자, 준(準)은 수평을 맞추는 밀대, 승(繩)은 먹줄입니다. 모두 기준과 관계가 있습니다.
칙(則)은 패(貝)와 도(刀)가 합한 글자입니다. 이때의 패(貝)는 솥을 뜻하는 정(鼎)의 원글자라 합니다. 솥 면에 칼로 글을 새겨 이를 지키도록 한 데서 칙(則)이 나왔습니다. 규(規)나 칙(則)이나 지켜야 할 법도임이 분명합니다.
https://www.lawtimes.co.kr/opinion/59472
천원지방(天圓地方)은 하늘은 둥글고(圓) 땅은 네모(方)라는 말이다. 옛날 동전인 상평통보의 가운데 네모난 구멍을 낸 까닭이다. 규(規)로 원을 그리고 칙(則)으로 네모를 그린다.

『주비산경』권상5 에 “네모는 땅에 속하고, 원은 하늘에 속한다. 하늘은 둥글고 땅은 네모나다.”(方屬地圓屬天天圓地方)고 했고, 또한 주공이 “수가 어디에서 나왔는가?”하고 묻자, 이에 대해 상고가 卷上2에서 “수의 법은 원과 방에서 나온다. 원은 방에서 나오고, 방은 구에서 나오며, 구는 구구 팔십일에서 나온다.”고 대답한다(數之法出于圓方 圓出 于方方出于矩矩出于九九八十一)
주비산경에는 아래 그림은 '구고현 정리'를 나타낸다.
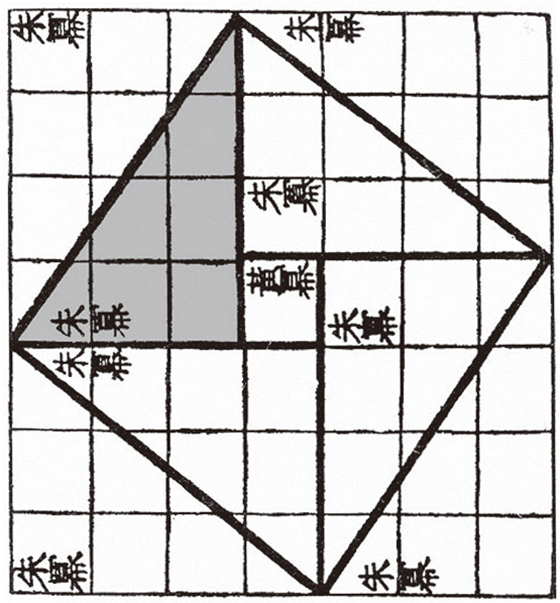
주비산경』권상2에 구고현(句股弦) 정리가 있다. “구를 잘라서 밑변(句)의 길이를 3으로 하고, 높이를 4로 하며, 빗변을 5로 만든다.”(故折矩以為句廣三股修四徑隅五)이 때 句는 삼각형의 밑변으로 3이고, 股는 삼각형의 높이로 4가 되며 弦은 삼각형의 빗변으로 5가 된다고 한다. 그런데 왜 각각 3, 4, 5로 했는지는 바로 원과 방의 이치 때문이다. 원의 지름이 1일 때 원의 둘레는 3이 되는데, 이것은 원주율($\pi$)을 3으로 보았기 때문이다. 바로 원의 둘레 값 3을 구(3)로 보았기 때문이다. 방(정사각형) 경우는 한 변의 길이를 1이면 둘레는 4가 되어 이를 고 (4)라 했다. 이는 수학의 기본 도형을 원과 방으로 보았고, 원과 방이 의미하는 천지가 만물의 근원임을 나타내는 것이다.
더 많이 알고 싶다면 아래 다큐멘터리를 보자. 이런 다큐가 좋아지면 수학은 저절로 잘 하게 되지 않을까 싶다.
반응형