수학 문제란?
수준은 중3 정도인 문제다.
문제 정삼각형 $ABC$의 내부에 있는 점 $P$에서 세 변에 이르는 거리의 합이 10이라고 할 때, 이 삼각형의 넓이를 구하시오.
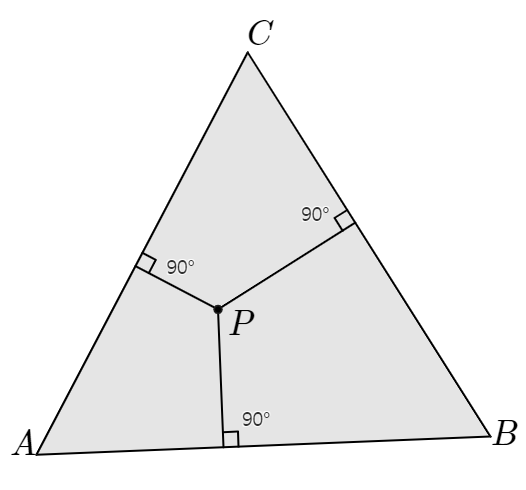
풀이 삼각형의 넓이는 밑변과 높이를 알면 구할 수 있다.
한 변의 길이를 $a$라고 하자.
넓이를 구하는 모든 문제는 잘라 붙이기로 해결할 수 있다. 넓이를 구하는 일은 결국은 넓이가 1인 정사각형으로 잘라 재배치하는 일이기 때문이다. 심지어 고등학교에서 배우는 정적분도 결국은 잘라 붙이기이다.
변과 평행인 아래 점선을 따라 자른 다음 이어 붙이면 높이가 10 임을 쉽게 알 수 있다.

따라서 $a\sin 60^{\circ}=10$에서 $$a=10\times \frac{2}{\sqrt3}$$이다. 따라서 넓이 $A$는
$$A=\frac{1}{2}\times 10 \times \frac{2}{\sqrt3}\times 10=\frac{100\sqrt3}{3}$$
평범한 학생에게 점선을 따라 잘라 붙이는 과정을 알아채는 일은 매우 어렵다.
이럴 때 공식이 필요하다.
한 변의 길이가 $a$인 정삼각형의 넓이는
$$\frac{a^2\sin 60^{\circ}}{2}=\frac{\sqrt 3 a^2}{4}\tag{1}$$
이다.
한편 각 변에 이르는 거리를 각각 $l,\;m,\;n$으로 놓으면 아래와 같이 넓이를 구할 수 있다.
$$\frac{1}{2} a(l+m+n)\tag{2}$$
(1), (2)를 사용하면 아무 생각 없이 답을 찾을 수 있다.
이런 장점 때문에 공식을 수도 없이 만들고 외운다.
삼각형의 넓이를 구하는 공식도 여러 가지다.
하지만 사람의 뇌는 단순한 암기로 쉽게 기록한 자료는 쉽게 지워지도록 진화했다.
공식은 외우는 것이 아니라 필요할 때 만들어 써야 하는 까닭이다.
이래서 수학이 어렵다. ㅠㅠ