방정식과 항등식
수학을 가르칠 때, 많은 학생이 용어를 제대로 정리하고 있지 않음을 알게 된다. 문제를 잘 푸는 학생이라 당연히 알고 있을 것 같은데 막상 물어보면 방정식과 같은 용어조차 명확하게 파악하고 있지 않을 때가 있다. 무슨 학문이든 용어를 명확하게 정의하고 시작하여야 한다. 특히 수학은 더욱 그렇다. 뜻도 모른채 문제만 푸는 일은 바둑으로 치자면 아무 생각없이 기보를 따라 돌을 놓는 일과 같다.
방정식의 뜻
대한수학회 수학용어 사전에서 방정식을 열쇠말로 검색하니 아벨방정식부터 시작한 목록은 백 개를 가뿐히 넘긴다.
kms 대한수학회
www.kms.or.kr
방정식은 영어로 'equation'이다.

한자로 적으면 方程式이다. 방정(方程)은 옛 중국 수학책 '구장산술'에도 등장한다. 네이버 국어사전은 '1. 수학 어떤 문자가 특정한 값을 취할 때에만 성립하는 등식.'으로 다음 사전은 '미지수가 포함된 식에서, 그 미지수에 특정한 값을 주었을 때에만 성립하는 등식'으로 적었다.
네이버가 좀 더 간결하다. 어떤 문자는 미지수로 부르는 것은 방정식이 있고 난 다음의 일이다. 어쨌든 방정식은 문자를 포함한 등식이다. 문자가 많으면 어려우니까 문자가 한두 개인 것을 먼저 공부한다.
참고 $x$를 미지수를 나타내는 대표적인 문자로 고른 까닭은 책을 인쇄할 판본을 만들 때 남아도는 활자였기 때문이란다. 요즘 젊은 세대를 $MZ$로 부르듯이 옛날에는 새로운 세대란 뜻으로 1970년대 태어난 이들을 $X$세대라 불렀다. 어디로 튈지 모르는 신세대라 미지수처럼 보인다는 뜻이었다. 그랬던 세대가 이제는 꼰대라 불리는 뻔한 세대 취급을 받고 있으니 세월이 무상하다.
다시 본론으로 돌아가자. 등식을 방정식으로 다루기 위해선 어떤 문자를 미지수로 볼 것인가 정해야 한다.
$$ax^2 +c=0\tag{1}$$
(1)은 $x$에 대한 이차방정식이지만 $a$나 $c$에 대한 일차방정식으로 보아도 된다. 대체로 상수는 $a,b,c$를 쓰고 미지수는 $x,y,z$로 나타낸다. 중고등학교에선 $x$를 미지수로 보면 되지만 때에 따라 잘 정해주어야 한다. 귀찮더라도 무엇에 대한 방정식인가를 늘 생각하는 것이 좋다.
먼저 $x$에 대한 방정식을 아래와 같이 정리하자.
$x$에 대한 방정식은 미지수 $x$에 따라 참과 거짓이 성립하는 등식이다. 방정식이 참이 되도록 하는 $x$의 값을 이 방정식의 '근' 또는 '해'라고 한다. 방정식의 해를 구하는 것을 '방정식을 푼다'고 한다.
모든 $x$에 대한 방정식은 잘 정리하면 $f(x)=0$꼴로 정리할 수 있다. 이때 식 $f(x)$에 따라 방정식을 분류한다. 다항식이면 다항방정식, 분수식이면 분수방정식, 미분이 있으면 미분방정식과 같이 분류한다. 다항방정식은 다시 차수에 따라 일차방정식, 이차방정식, 삼차방정식 등으로 나눈다.
$$x^2+3x-4=0\tag{2}$$
(2)는 $x$에 대한 이차방정식이다. 등식을 참이 되게 만드는 $x=1$ 또는 $x=-4$가 해이다. 이 해를 구하는 과정을 방정식을 푼다고 한다.
$$3x+2x=5x\tag{3}$$
(3)은 (2)와 달리 $x$의 값에 관계없이 항상 참이다. 모든 수가 해이므로 굳이 해를 구할 이유가 없다. 이런 등식을 항등식이라고 한다. 문자를 포함한 등식은 방정식과 항등식 두 갈래로 나눌 수 있다.
항등식의 뜻
주어진 등식의 문자에 어떤 값을 대입해도 항상 성립하는 등식을 그 문자에 대한 항등식이라고 한다.
주로 곱셈 공식이나 인수분해 공식으로 불리는 등식이다.
$$(a+b)(a-b)=a^2 -b^2$$
$$a^3-b^3=(a-b)(a^2 +ab+b^2)$$
아래와 같은 과정을 보면 모양은 다르지만 내용은 같은 식을 찾는 과정을 되풀이 한다. 수학 문제를 해결하는 과정은 항등식을 잇달아 찾아내 식을 간단하게 만드는 과정이다.
$$\begin{split}x^2 y+x^3 -x-y&=x^2 (x+y)-(x+y)\\&=(x^2 -1)(x+y)\\&=(x-1)(x+1)(x+y)\end{split}$$
수를 복소수 범위까지 확장하면 모든 다항식을 일차식의 곱으로 나타낼 수 있다. 아무리 복잡한 다항식도 모두 간단한 일차식으로 바꿔서 해결할 수 있으니 이 얼마나 아름다운가!
항등식에서 가장 많이 나오는 문제는 나머지 정리와 인수정리이다.
예제. 다항식 $x^3 +ax^2 +bx+1$을 $x^2 -1$로 나눈 나머지가 $x+1$일 때, $a^2 +b^2$의 값을 구하여라.(단, $a,\,b$는 상수이다.)
괄호 안에 $a,\,b$는 상수라고 했으니 몫을 $Q(x)$라고 하면 아래와 같이 $x$에 대한 항등식을 적을 수 있다.
$$x^3 +ax^2 +bx+1=(x^2 -1)Q(x)+x+1\tag{4}$$
직접 나누어 몫과 나머지를 구해도 되지만 몫을 구하지 않고도 구할 수 있다. 항등식은 $x$에 어떤 값을 넣어도 성립하므로 $x^2 -1=0$인 값을 대입하면 된다.
$x=1$이면 $1+a+b+1=2$
$x=-1$이면 $-1+a-b+1=0$
$a=-1,\,\,b=1$이므로 $a^2 +b^2 =2$이다.
연립이차방정식
위에서 밝혔듯이 어떤 문자를 미지수로 볼 것인가는 자유롭다. 당연히 미지수는 둘 이상일 수 있다.
$$2x+y=3\tag{5}$$
(5)는 미지수가 둘이므로 해는 순서쌍 $(x,y)$로 나타낼 수 있다. 이 방정식은 해가 무수히 많은데 그래프는 직선이므로 보통 직선의 방정식으로 부른다. 아래와 같은 이차함수도 방정식으로 볼 수 있다.
$$y=x^2 +2x+3\tag{6}$$
방정식은 최고차항의 차수를 차수로 한다. 당연히 (5)와 (6)을 동시에 만족하는 공통해를 구할 수 있다. 중학교에서 배운 연립방정식을 생각하면 쉽다.
미지수 $y$를 소거하기 위해 (5)-(6)을 하자.
$$2x=-x^2 -2x$$
$$x^2 +4x=0$$
$x=0$ 또는 $x=-4$
(6)에 대입하여
$$\cases{x=0\\y=3}\,\,\,\text{또는}\,\,\,\cases{x=-4 \\ y=11}$$
를 얻을 수 있다.
이때, 해를 좌표로 표현할 수 있다. 즉, $(0,3)$과 $(-4,11)$을 얻는다. 기하로 해석하면 (6)의 그래프인 포물선과 (5)의 그래프인 직선은 두 점 $(0,3)$과 $(-4,11)$에서 만난다.

아래와 같은 연립방정식도 있다.
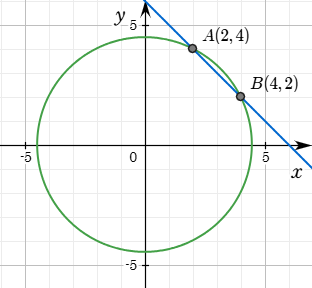
$$\cases{x+y=6\,\,\,\cdots\cdots(1)\\x^2 +y^2 =20\,\,\cdots\cdots(2)}$$
(1)을 정리한 $y=6-x\,\,\,\cdots(3)$을 (2)에 대입하면
$x^2 +(6-x)^2 =20,\,\,\,x^2 -6x+8=0$
이것을 풀면 $x=2$ 또는 $x=4$이다.
(3)에 대입하여
$$\cases{x=2\\y=4} \,\,\,\text{또는}\,\,\, \cases{x=4\\y=2}$$
를 얻을 수 있다.
참고로 (2)는 중심이 원점이고 반지름은 $2\sqrt5$인 원의 방정식이다.