별자리 그리기
밤하늘을 가만히 쳐다보고 있으면 별이 점점 많아진다.
"청천 하늘엔 잔별도 많고요 우리네 가슴속엔 눈물도 많다. 아리 아리랑 쓰리 쓰리랑 아라리가 났네"
진도 아리랑이다. 요즘 사람들은 별을 볼 일이 없다. 아주 가끔 캠핑이라고 가면 밤하늘에 반짝이는 별을 보며 감상에 잠긴다. 아주 오래전에 군대에서 보초 서면서 보았던 밤하늘엔 별이 보기 좋았다. 전기도 없던 시절엔 사람들이 별을 보는 일이 많았을 것이다. 옛사람들이 별을 보며 만든 수많은 이야기가 있다. 별이 워낙 많아서 하나하나 자리를 외우기 쉽지 않으니 여러 별을 묶어서 별자리를 만들고 이름을 붙였다. 카시오페아, 헤라클레스, 페르세우스, 큰곰자리, 백조자리, 사냥개자리 $\cdots$

한데 묶인 별자리 가운데 가장 밝게 보이는 별을 '알파별'이라 불렀다. $\alpha$는 그리스 알파벳 첫 글자이다. 훗날 밝기를 정밀하게 재 보니 가장 밝지 않은 '알파별'도 있다고 한다.
중학교 1학년 기본 도형 점, 선, 면을 배운다. 별자리 그림으로 점, 선, 면을 다루고자 한다. 별자리 가운데 황도 12궁이 있다. 태어난 때에 따라 별자리를 정할 때 쓴다. 요즘은 음력 생일을 가진 아이가 없으니 태어난 별자리도 찾기 쉽다. 24절기가 있는데 차례로 둘씩 묶어서 황도 12궁이 된다.

이제 별자리 그림을 수학과 연결지어 보자.
선의 끝은 점이다. 따라서 선과 선이 만나는 곳은 점이다. 선의 끝이나 선과 선이 만나는 점을 꼭짓점이라고 하자. 점과 점을 잇는 선분을 변이라고 하자. 변으로 둘러싸인 영역은 면이라고 하자. 영어로 꼭짓점은 vertec, 변은 edge, 면은 face이므로 꼭짓점, 변, 면 각각의 개수를 v, e, f로 나타내자.
처녀자리는 $v=14,\;\; e=14,\;\; f=1$이다. 별자리를 보고 각각 $v,\;\; e,\;\; f$를 구해보자. $v-e+f=1$ 임을 확인해 보자.
아래와 같은 평면 도형에서도 확인해 보자.
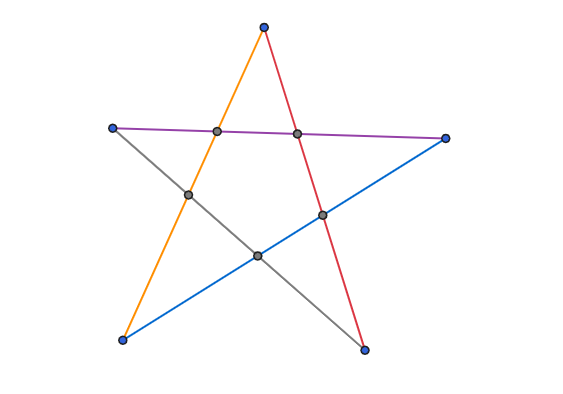
물음. 평면 도형은 모두 $v-e+f=1$를 만족하는가? 어떻게 증명할 수 있을까?
오일러 정리는 공간도형에서는 $v-e+f=2$가 성립한다는 정리이다. 링크를 눌러서 증명을 확인해 보자.
https://horoscopes.lovetoknow.com/about-astrology/constellations-zodiac
Constellations and the Zodiac | LoveToKnow
Even if you're skeptical about the validity of astrology, reading about and understanding the nature of the constellations and their historical relationship with the 12 signs of the astrological zodiac can be fascinating. Constellation Aries: The Ram Over
horoscopes.lovetoknow.com
참고: 별자리는 constellation, 황도는 천구에서 태양이 지나는 자리에 동물을 자리매김한 그리스말에서 온 zodiac, 별자리 점성술은 horoscope이다. 아무래도 우리말보다는 영어로 찾을 때 더 많은 자료가 검색된다.