삼각형의 내심과 헤론의 공식
모든 다각형은 잘라서 삼각형으로 나눌 수 있다. 따라서 삼각형의 넓이를 구하는 일은 매우 중요하다. 여기에 삼각형 넓이를 구하는 몇 가지 공식을 정리해 두려고 한다. 중학교 3학년을 마치면 이해할 수 있도록 설명하고자 한다. 따라서 증명 과정이 지루할 수 있고 때로는 약간의 비약이 있을 수 있다.
시작_밑변과 높이의 길이를 알 때
초등학교에서 삼각형 넓이를 구하는 공식을 배운다. 사실 초등학교 수준에서 이 공식을 완벽하게 이해하기는 쉽지 않지만 대부분 학생은 일단 외워서 잘 사용하고 있다.
삼각형 넓이$=\displaystyle{\frac {1}{2}}\times$ 밑변 $\times$ 높이
중학교에선 문자와 식을 배우니까 삼각형 $ABC$의 넓이 $A$는 아래와 같이 표현한다. 평행사변형의 성질을 배우고 나면 증명할 수 있다.

$$A=\frac{1}{2}ah\tag{1}$$
발전_내접원의 반지름과 세 변의 길이를 알 때
중학교 2학년에서 내심을 배우고 나면 삼각형의 넓이를 구하는 또 다른 공식을 하나 알게 된다. 먼저 그림과 같이 $\triangle ABC$의 내심을 $I$라고 하고 세 변에 내린 수선을 발을 각각 $D$, $E$, $F$라고 하자.
내심의 성질에 따라 $\overline{ID}=\overline{IE}=\overline{IF}$이고 이들은 내접원의 반지름의 길이와 같다.

내접원의 반지름을 $r$이라 놓자. (참고: 수학책에서 편하게 나타내기 위해 변의 길이는 아래와 같이 대각의 이름(건너편 꼭짓점 이름)을 소문자로 나타낸다.)
$$\overline{BC}=a,\;\;\overline{CA}=b,\;\;\overline{AB}=c$$
전체 삼각형의 넓이는 내심과 꼭짓점을 잇는 선분으로 나누어지는 세 삼각형의 넓이를 더한 것과 같다. 이것을 정리하면 삼각형의 넓이를 구하는 새로운 공식을 얻을 수 있다.
$$\begin{split}\triangle ABC&=\triangle IBC+\triangle ICA+\triangle IAB\\&=\frac{1}{2}\times a\times r+\frac{1}{2}\times b\times r+\frac{1}{2}\times c \times r\end{split}$$
$$\therefore \;\;A=\frac{1}{2}r(a+b+c)\tag{2}$$
중학생은 여기까지만 알면 된다. 그래도 욕심이 난다면 몇 가지 공식을 더 만들어 보자.
그림 (2)에서 몇 가지 성질을 정리해 두자.
이제 간단하게 나타내기 위해 $$\frac{1}{2}(a+b+c)=s\tag{2.1}$$라고 하자.
한 점에서 원에 그은 접선은 길이가 같으므로
$$\overline{BD}=\overline{DC},\quad \overline{CE}=\overline{EA},\quad\overline{AF}=\overline{FB}$$
이다. 따라서
$$2\overline{BD}=a+b+c-(\overline{AF}+\overline{EA}+\overline{CE}+\overline{DC})=a+b+c-2b$$
$$\overline{BD}=\overline{BF}=\frac{1}{2}(a+b+c)-b=s-b\tag{2.2}$$
마찬가지로
$$\overline{CE}=\overline{CD}=s-a\tag{2.3}$$
$$\overline{AF}=\overline{AE}=s-c\tag{2.4}$$
다음_세 변의 길이를 알 때
삼각형의 내심과 헤론의 공식
이제 그림을 덧붙여 그린다. 점 $I$는 내심이다. 점 $O$는 두 외각의 이등분선이 만나는 점이다. 이 점을 방심이라고 하는데 우리나라 교육과정에선 이제 배우지 않는다. 이름은 그다지 중요하지 않다. 방심에서 한 변과 다른 두 변의 연장선에 이르는 거리가 같다. 이것도 증명할 수 있지만 이글에선 생략한다.
$$\overline{OL}=\overline{OM}=\overline{ON}=r_1$$

$$\overline{BL}=\overline{BN}\tag{3.1}$$
$$\overline{AL}=\overline{AM},\;\;\;\overline{CM}=\overline{CN}$$
$$\therefore\quad \overline{BL}+\overline{BN}=a+b+c\tag{3.2}$$
(3.1)와 (3.2)에 따라
$$\overline{BL}=\overline{BN}=\frac{1}{2}(a+b+c)=s$$이다. 위에서 $(a+b+c)/2=s$라고 하였으므로 공식 (2)를 다시 적으면 $A=rs$이다. 이제 $r$을 $s$로 나타낼 수 있다면 세 변의 길이만으로 삼각형의 넓이를 구할 수 있게 된다. 새로운 공식을 만들 수 있는 것이다. 먼저 아래를 확인하자.
$$\overline{BD}=s-b,\quad \overline{DC}=s-a, \quad \overline{CN}=s-a$$이다.
$\triangle{BDI}$와 $\triangle{BNO}$는 닮음이다.
$$\overline{BD}:\overline{ID}=\overline{BN}:\overline{NO}$$
$$s-b:r=s:r_1$$
$$rs=r_1(s-b)$$
$$r_1=\frac{rs}{s-b}\tag{3.3}$$
$\triangle{IDC}$와 $\triangle{CNO}$는 닮음이다.
$$\overline{ID}:\overline{DC}=\overline{CN}:\overline{NO}$$
$$r:s-a=s-c:r_1$$
$$rr_1=(s-a)(s-c)\tag{3.4}$$
(3.3)과 (3.4)에서 $r_1$을 소거하자.
$$r^2=\frac{(s-a)(s-b)(s-c)}{s}$$
$$r=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}}\tag{3.5}$$
바라던 대로 $r$을 대칭 구조를 가진 예쁜 식으로 정리했다. (2)에 대입하면 새로운 공식을 얻는다.
$$A=\sqrt{s(s-a)(s-b)(s-c)}\tag{3}$$
공식 (3)은 헤론의 공식으로 널리 알려졌다.
피타고라스 정리와 헤론의 공식
이 공식을 증명하는 여러 가지 방법이 있다. 피타고라스 정리를 이용해서 공식을 만들 수 있다. 아마도 헤론은 이 방법을 쓰지 않았을까?
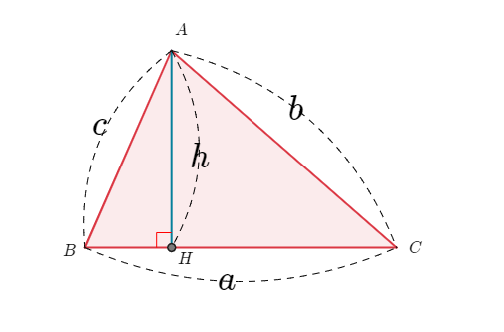
(1)에서 $h$를 세 변의 길이로 나타내면 된다.
먼저, $\overline{BH}=x$라고 하자. 피타고라스 정리에 따라
$$h^2=c^2 -x^2=b^2-(a-x)^2$$
이다. 이를 정리하면
$$c^2 -x^2=b^2-a^2+2ax-x^2$$
$$x=\frac{a^2+c^2-b^2}{2a}$$
$$h^2=c^2 -\left(\frac{a^2+c^2-b^2}{2a}\right)^2$$
이다.
$$\begin{split}A^2&=\frac{1}{4}a^2 h^2\\&=\frac{1}{4}a^2\left(c^2 -\left(\frac{a^2+c^2-b^2}{2a}\right)^2\right)\\&=\frac{4a^2c^2-(a^2+c^2-b^2)^2}{16}\\&=\frac{(2ac+a^2+c^2-b^2)(2ac-a^2-c^2+b^2)}{16}\\&=\frac{((a+c)^2-b^2)((b^2-(a-c)^2)}{16}\\&=\frac{(a+b+c)(a+c-b)(b+a-c)(b-a+c)}{16}\\&=\frac{2s(2s-2b)(2s-2c)(2s-2a)}{16}\\&=s(s-a)(s-b)(s-c)\end{split}\tag{3.6}$$
정리하면 (3)과 같은 식을 얻는다.
절정_두 변의 길이와 끼인 각의 크기를 알 때
중학교 3학년에서 삼각비를 배운다. 삼각비를 배우면 두 변과 사이에 끼인 각의 크기만 알면 넓이를 구할 수 있다. 사실 삼각비는 피타고라스 정리를 쉽게 활용하기 위해 고안한 것과 마찬가지다.
위 그림에서 아래와 같이 나타낼 수 있다.
$$\sin B=\frac{h}{c},\quad\sin C=\frac{h}{b}$$
(1)을 다시 정리하자. 각의 크기와 혼동을 피하기 위해 넓이를 $S$라고 하자.
$$S=\frac{1}{2}ah=\frac{1}{2}ac \sin B =\frac{1}{2}ab\sin C=\frac{1}{2}ab\sin C\tag{4}$$
여기서부터는 고등학생에게 알맞은 수준이다. 뭐 중학교 3학년 1학기를 마쳤다면 이해할 수 있을 것이다.
아래에 있는 원은 삼각형의 외접원이다. 외접원의 반지름의 길이를 $R$로 놓으면 아래와 같은 사인법칙이 성립한다.

$$\sin A=\frac{a}{2R},\quad \sin B=\frac{b}{2R},\quad\sin C=\frac{c}{2R}\tag{sine law}$$
$$S=\frac{abc}{4R}\tag{4.1}$$
내심은 덧셈과 외심은 곱셈과 연결된다. 이래서 수학은 참 아름답다.
한편 코사인 법칙은 아래와 같이 표현할 수 있다.
$$\cos B=\frac{a^2+c^2-b^2}{2ac}\tag{cosine law}$$
$$\sin B=\sqrt{1-\cos^2 B}$$
정리하는 과정은 (3.6)을 정리하는 과정과 같다.
각의 크기보다는 변의 길이를 측정하는 일이 더 쉽다. 따라서 삼각형의 넓이를 구할 때 세 변의 길이만 알면 되는 헤론의 공식을 쓰는 것이 쉬울 것이다. 뭐 요즘이야 정밀한 측량 도구가 있고 정확하고 빠른 계산기가 있으므로 오차가 거의 없을 것이다. 하지만 고대엔 헤론의 공식으로 넓이를 구하는 기술은 아무나 흉내 낼 수 없는 최첨단 기술이었음이 분명하다. 교육과정에서 코사인 법칙도 빠져서 좀처럼 구경하기 어렵다. 학교 공부하다가 살짝 뭔가 부족함이 느껴지면 아래 링크를 열어 공부해 보자.
사인, 코사인 법칙
사인법칙 삼각비를 이용하여 삼각형의 세 변의 길이와 세 각의 크기 사이의 관계를 알아보자. 삼각형 $ABC$에서 $\angle A ,\; \angle B,\; \angle C$의 크기를 각각 $A,\; B,\; C$로 나타내고, 이들의 대변의
suhak.tistory.com