제곱근 2는 유리수가 아니다
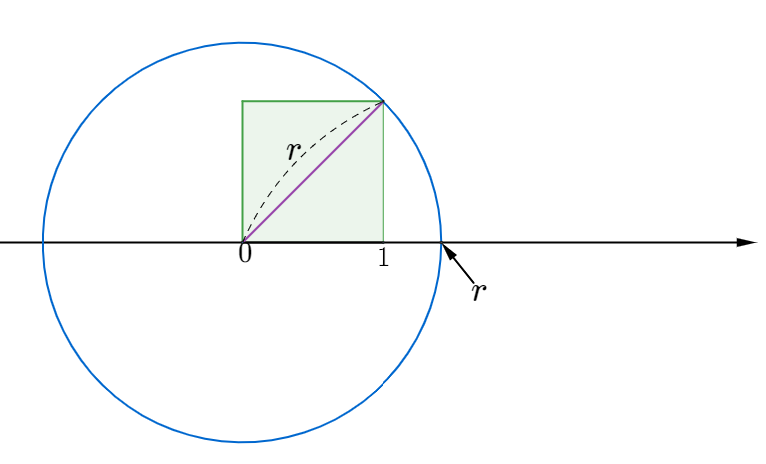
제곱해서 2가 되는 수가 있는가는 피타고라스 정리로 쉽게 확인할 수 있다. 아래 그림과 같이 수직선 위에 한 변의 길이가 1인 정사각형의 대각선의 길이에 해당하는 점이 존재한다.
$$r^2=1^2+1^2=2$$
고대 바빌로니아를 비롯한 여러 문명에서 이 대각선의 길이를 구하기 위한 도전이 이어졌다.
피타고라스 학파는 자연수의 비율로 나타낼 수 없는 양을‘잴 수 없는 양’ 이라고 불렀고, 수에 포함시키지 않았다. 그리고 이런 유리수가 아닌 수의 존재를 숨겼다. 프로클로스의 글은 이러한 정황을 잘 보여 준다.
감춰져 있던 유리수가 아닌 수를 처음으로 공개하는 사람은 파멸하여 죽을 것이다. 그것은 모두에게 적용될 것이다. 말로 표현할 수 없는 것과 형체가 없는 것은 감추어질 필요가 있기 때문이다.
피타고라스 학파였던 수학자 히파소스는 대각선의 길이는 자연수의 비로 나타낼 수 없는 무리수임을 알아내고 바깥으로 알렸다는 까닭으로 동료들에게 암살되었다고 전해진다.
https://suhak.tistory.com/1450
YBC7289와 무리수 $\sqrt{2}$
차례 고대 바빌로니아인은 점토판에 정보를 새겼다. YBC7289 점토판은 기원전 1800년에서 1600년 사이에 남부 메소포타미아에 살던 어떤 학생이 남긴 것으로 여겨진다. 아래 사진과 같이 정사각형을
suhak.tistory.com
다들 정답을 알고 있지만 갑자기 물으면 말문이 막히는 문제가 있다.
$\sqrt {2}$는 무엇인가?
정답은 "제곱해서 2가 되는 양수"이다. 여기서 1.414니 뭐 이런 대답을 하면 실력 부족이다.
$\sqrt{2}$는 왜 유리수가 아닌가?
요즘은 그냥 $\sqrt{2}$는 무리수라고 하자로 시작하지만 아주 먼 옛날엔 중학교 교과서에는 증명이 있었다. 뭐 그렇게 어려운 증명이 아닌데 왜 교육과정에서 다루지 않는지 모르겠다. 아무튼 이제는 대학에서 수학을 전공하는 이들만 만나는 증명이 되어 버렸다.
$r^2=2$를 만족하는 유리수 $r$는 존재하지 않는다.
증명 유리수는 서로소인 두 정수의 분수꼴로 나타낼 수 있는 수이다.
이제 $r^2=2$이고 $r=p/q$라고 가정하자. (단, $p,\;\;q$는 서로소인 정수, $q\not=0$)
$$\left(\frac{p}{q}\right)^2=2$$
$$p^2 =2q^2\tag{1}$$
$p^2$이 2의 배수이므로 $p$도 2의 배수이다.
$p=2m$이라고 하면 (1)에서
$$(2m)^2=2q^2,\quad \therefore q^2=2m^2$$
$q$도 2의 배수이다.
$p,\;\;q$는 서로소라는 가정에 모순이다.
따라서 $r^2=2$를 만족하는 유리수는 존재하지 않는다.
$\blacksquare$
사실 엄밀한 증명은 아니다. 엄밀함을 위해선 아무래도 집합을 도입해야 하는데 중학교 수준에 맞지 않는다고 판단했을 것이다. 올바른 판단이긴 하다. 하지만 교육과정이 너무 쉬워서 중학생 가운데 수학적 재능이 뛰어난 학생에겐 어떤 흥미도 유발하지 못하고 있어 안타깝다. 그렇다고 평범한 학생까지 고생스럽게 수학을 공부해야 한다고 생각하진 않는다.
다만 누군가는 어린 시절에 수학에 흥미를 가지고 평생을 연구할 주제를 찾을 수도 있어야 한다. 그래야 우리나라 기초과학 특히 수학 분야에 인재가 유입될 수 있다. 요즘 미국에 가지 않고 태어난 나라에서 수학을 제대로 공부할 수 있는 나라가 거의 없다. 그래서 미국이 세계 최강이고 당분간 어떤 나라도 역전시키지 못하는 까닭이다.
https://suhak.tistory.com/1461
유리수는 완비(complete)가 아니다
해석학 책에 있는 일부를 옮겨 놓는다. 정의 유리수 집합에서 반직선(ray)은 다음과 같은 성질을 만족하는 유리수 $\mathbb{Q}$의 부분집합 $U \subset \mathbb{Q}$이다. (a) $x\in U$이고 $y>x$이면 $y\in U$이다.
suhak.tistory.com