킬리만자로의 높이를 재는 방법
우연히 읽은 기사가 재밌어서 연결해 놓는다.
요약하면 네팔과 중국이 공동으로 에베레스트산의 높이를 새로 쟀는데 이전과 달라졌다는 이야기와 함께 지구 중심으로부터 재거나 바닥으로부터 재면 에베레스트보다 더 높은 산이 있다는 이야기가 함께 있다.
아주 먼 옛날에도 산에 오르지 않고 높이를 재는 방법이 있었다는 걸 아는가?

먼저 중학교에서 배우는 삼각비를 이용하여 간단하게 건물이 높이를 잴 수 있다.
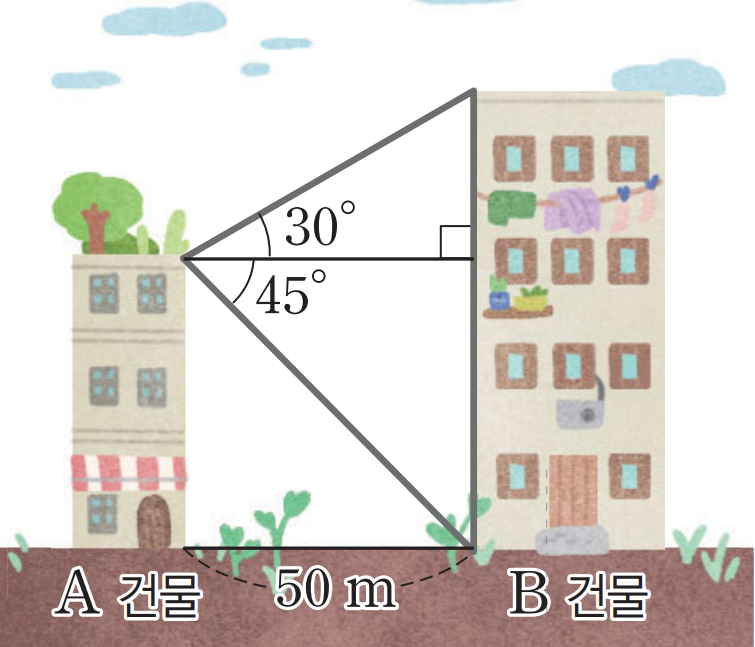
A건물의 높이는 50m이다. B건물의 높이는 여기에 $50\tan 30^{\circ}$를 더한 값이다.
$$50+50\tan 30^{\circ}=50\left(1+\frac{\sqrt3}{3}\right)$$
이런 문제에서 두 건물 사이의 거리인 50m를 재는 일은 어렵지 않다. 하지만 산의 높이를 잴 때는 다르다. 관측지점에서 산꼭대기에서 해수면에 내린 수선의 발까지 거리를 알아야 하는데 이걸 재는 일이 어렵다.

먼저 킬리만자로처럼 평지에 우뚝 솟아 있다고 가정하자. 이것도 짐작이다. 킬리만자로엘 가본 적이 없으니 말이다. 아무튼 수학 문제에서 가정은 자유다.
아래 그림에서 산꼭대기는 $A$, 관측자 위치는 $B$, 지면에 내린 수선의 발은 $C$라고 하자.
이미 말한대로 $B$에서 $A$를 올려단 본 각 $\alpha$는 측정할 수 있지만 $\overline{BC}$는 측정할 수 없다. 이때 또 다른 관측 지점 $D$를 잡는다. 자 이제 어떤 것을 측정할 수 있는가?

두 각 $\beta,\;\;\gamma$와 $\overline{BD}$를 측정할 수 있다. 고등학교에서 배우는 사인법칙을 이용하여 $\overline{BC}$를 구하면 중학교에서 배운 삼각비로 $h$를 구할 수 있다.
$$\angle C=\pi-(\beta+\gamma)$$
$$\frac{\overline{BC}}{\sin\gamma}=\frac{\overline{BD}}{\sin \angle C}$$
$$\overline{BC}=\frac{\overline{BD}\sin\gamma}{\sin (\beta+\gamma)}$$
$$h=\overline{BC}\tan\alpha=\frac{\overline{BD}\sin\gamma\tan\alpha}{\sin (\beta+\gamma)}$$
https://www.hani.co.kr/arti/science/science_general/973902.html
86cm 높아진 에베레스트...더 높은 산이 있다?
www.hani.co.kr