닮음과 피타고라스 정리
이글도 '선행 학습'에 빠져서 제대로 된 수학 공부를 하지 않는 중학생을 위해 쓰는 글이다. 먼저 용어를 하나 정리해 보자. 직각이 무엇이냐고 물으면 대부분은 90도가 직각이라고 대답한다. 왜 90도인 각을 직각이라고 하느냐고 묻는다면 어떻게 대답해야 할까? 대부분 중요하게 여기지 않고 지나치지만 모든 교과서에는 용어가 잘 설명되어 있다. 수학 교과서의 교과서는 고대 그리스 수학자 유클리드가 쓴 '원론'이다.
직각이란 무엇인가?
영어로 직각은 right angle이다. 그대로 옮기면 '바른 각'이다. 삐뚤어지지 않은 각이란 뜻이다. '원론'에서 직각을 아래와 같이 정의하였다.
Definition 10.When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
직선에 서 있는 한 직선이 만드는 이웃한 각이 서로 같을 때, 두 각은 직각이다. 그리고 다른 직선에 서 있는 직선을 수선이라고 부른다.
바로 서 있던 수선이 한쪽으로 기울면 예각과 둔각이 생긴다. 삼각형을 덧붙이면 여러 가지 다각형을 만들 수 있다. 이렇게 보면 직각과 삼각형은 유클리드 기하의 바탕이다. 따라서 직각삼각형이 품고 있는 성질을 탐구하는 일은 수학을 공부하는 이에게 매우 중요한 과정이다. 직각삼각형이 품고 있는 성질 가운데 으뜸은 바로 직각삼각형의 세 변의 길이가 이루는 관계를 밝힌 피타고라스 정리이다.
각 $C$가 직각인 직각삼각형 $ABC$에서 세 변의 길이를 각각 $\overline{BC}=a,\;\;\overline{AC}=b,\;\;\overline{AB}=c$라고 하면 아래와 같은 관계를 이룬다.
$$a^2 +b^2 =c^2\tag{1}$$
워낙 유명한 정리라 이름은 대부분 알고 있지만 정확하게 뜻을 이해하고 있는 학생은 생각보다 적다. 중학교에서 단순 암기하고 문제 풀이에만 매달리면 훗날 고등학교에서 심화 문제를 다룰 때 큰 어려움을 겪게 된다. 따라서 피타고라스 정리를 이해하는 일은 중학생이 반드시 해야 할 중요한 일이다. 중요한 정리라 증명하는 방법이 매우 많다. 여기선 닮음으로 살펴보려고 한다.
직각삼각형은 잘라도 모양은 그대로...
원을 그리면 직각삼각형을 쉽게 얻을 수 있다. 지름을 빗변으로 다른 꼭짓점은 원둘레 위에 있는 삼각형을 그리면 직각삼각형이 된다. 모든 직각삼각형은 그림과 같이 직각인 꼭짓점에서 빗변에 내린 수선으로 나누어지는 두 삼각형은 모두 처음에 있던 삼각형과 닮음이다.
$$\triangle ABC \sim \triangle ACD\sim \triangle CBD$$

먼저 $\overline{AD}=x,\;\;\overline{DB}=y$라고 하자.
$\triangle ABC \sim \triangle ACD$이다. 따라서 $$\overline{AB}:\overline{AC}=\overline{AC}:\overline{AD}$$
$$c:b=b:x\quad \therefore x=\frac{b^2}{c}$$
$\triangle ABC\sim \triangle CBD$ 이다. 따라서 $$\overline{AB}:\overline{CB}=\overline{CB}:\overline{BD}$$
$$c:a=a:y\quad \therefore y=\frac{a^2}{c}$$
$x+y=c$이므로
$$\frac{b^2}{c}+\frac{a^2}{c}=c\tag{2}$$
이것을 정리하면 (1)과 같다. 제곱은 정사각형의 넓이로 생각할 수 있다. 따라서 (2)가 길이를 나타내는 식이라면 (2)는 넓이를 나타내는 식이다. 이것을 그림으로 나타낸다. 주로 정사각형인 그림을 보았을 것이다. 하지만 다른 정다각형을 바꾼다고 달라지는 것은 없다.
피타고라스 정리를 넓이로 생각하기


원이 된다고 하더라도 마찬가지다. 닮음인 도형의 넓이는 닮음비의 제곱과 같은 비를 이룬다.

중학교 3학년에서는 직각삼각형에서 세 변이 이루는 비를 아래와 같이 이름을 붙여서 삼각비로 다룬다.
$$\frac{b}{c}=\frac{x}{b}=\cos A,\;\;\;\frac{a}{c}=\frac{y}{a}=\sin A$$
피타고라스 정리는 고등학교에선 제2 코사인정리와 연결된다. 이처럼 중학교에선 앞으로 밟아야 할 과정을 위해 중학교 교과서에 나오는 공식을 이해하는 일에 힘써야 한다. 그런데 수많은 학생들이 선행이란 이름으로 고등학교 과정을 밟고 있다. 걷지도 못하는 애들을 뛰게 만드는 일과 마찬가지다. 대부분의 선행 학습은 쓸데없이 돈과 시간과 정력을 낭비하는 일이다. 아래 문제를 풀어보자. 삼각비를 배운 중학교 3학년이라면 잘 잘라서 붙이면 쉽게 해결할 수 있을 것이다.
잘 잘라서 붙이면 풀리는 문제
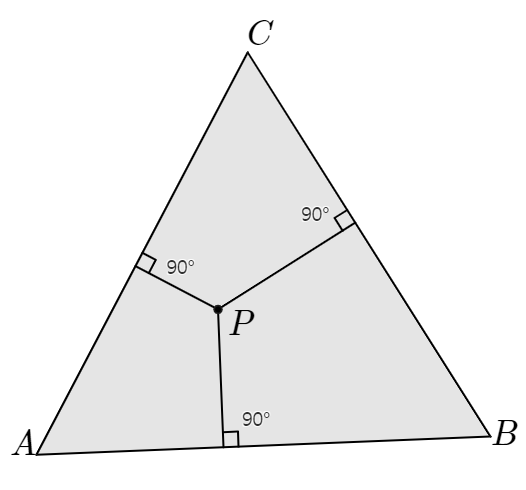
아래 삼각형 $ABC$는 정삼각형이다. 내부에 있는 점 $P$에서 세 변에 이르는 거리의 합은 $10$이다. 이 삼각형의 넓이를 구하시오.
수학 문제란?
수준은 중3 정도인 문제다.문제 정삼각형 $ABC$의 내부에 있는 점 $P$에서 세 변에 이르는 거리의 합이 10이라고 할 때, 이 삼각형의 넓이를 구하시오. 풀이 삼각형의 넓이는 밑변과 높이를 알면 구
suhak.tistory.com
피타고라스 정리는 어디에 쓸까?
학력이 중학교 2학년 이상이라면 누구나 한 번쯤은 '피타고라스(Pythagoras)'란 이름을 들어 보았다. 수학을 싫어하는 사람도 분명 뭔가 중요한 사람임을 알 것이다. 피타고라스는 워낙 많은 분야에
suhak.tistory.com
피타고라스 정리의 증명을 몇 가지 알고 있나요?
피타고라스 정리는 유클리드 원론에 등장한다. 유클리드 원론에 있는 명제 47과 48은 아래와 같다. Proposition 47.In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the
suhak.tistory.com
