 ko
ko 피타고라스 정리의 증명을 몇 가지 알고 있나요?
수학이야기/기하벡터 2013. 12. 10. 12:43피타고라스 정리는 유클리드 원론에 등장한다. 유클리드 원론에 있는 명제 47과 48은 아래와 같다.
Proposition 47.In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle. 직각삼각형에서 직각과 마주 보는 변을 가지고 정사각형을 만들면, 넓이는 나머지 다른 변으로 만든 정사각형 넓이를 더한 것과 같다.
Proposition 48.If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right. 어떤 삼각형이 있는데, 한 변을 가지고 만든 정사각형의 넓이가 다른 변으로 만든 두 정사각형 넓이를 더한 것과 같다면 다른 두 변 사이의 각은 직각이다.
직각삼각형은 세 변의 길이 사이에 피타고라스 정리가 성립하고 피타고라스 정리가 성립하는 삼각형은 직각삼각형이다. 어떤 삼각형이 직각삼각형이라는 조건과 변의 길이 사이에 피타고라스 정리가 성립한다는 조건은 필요충분조건이므로 같은 말이다.
피타고라스 정리를 증명하는 방법은 무척 많다. 몇 가지 정리해 둔다.

가장 널리 알려진 증명으로 유클리드가 '원론'에서 증명한 방법이다.
¯BC2+¯AC2=¯AB2
(Pythagorean Theorem)
a2+b2=c2

¯AB=¯AE,¯AF=¯AC,∠FAB=∠CAE
∴△ABF≡△AEC
◻FACG=2△FAC=2△ABF
◻EAML=2△EAM=2△ACE
∴◻FACG=◻EAML
마찬가지로
∴◻KBCH=◻DBML
∴◻FACG+◻KBCH=◻ABDE
◼
이 증명은 삼각형에서 두 꼭짓점을 고정하고 나머지 다른 꼭짓점을 고정된 변과 평행으로 이동하여 만드는 삼각형은 모두 넓이가 같다는 성질을 이용한다.
평행이동을 이용하면 모양은 다르지만 넓이가 같은 도형을 쉽게 만들 수 있다. 이런 성질을 증명에 활용하면 아주 좋다.
아래는 세 꼭짓점 A,B,C을 빗변의 길이 ¯AB 만큼 평행이동한 그림이다.

직사각형 AEFG와 평행사변형 A′ACC′은 넓이가 같다.
평행사변형 A′ACC′와 정사각형 HACI는 넓이가 같다.
∴◻AEFG=¯AC2
마찬가지로
∴◻GFDB=¯BC2
∴¯AC2+¯BC2=¯AB2
◼
위키피디아에 움직이는 그림으로 표현한 그림이 있다.

 |
 |
왼쪽 그림은 아래와 같이 증명할 수도 있다.
(a+b)2=4⋅12ab+c2
마찬가지로 오른쪽 그림은 아래와 같이 증명한다.
c2=4⋅12ab+(a−b)2

아래 첫 번째 그림에서 직각 삼각형 둘을 회전하면 두 번째 그림이 된다. 넓이는 달라지지 않으므로 a2+b2=c2이다.

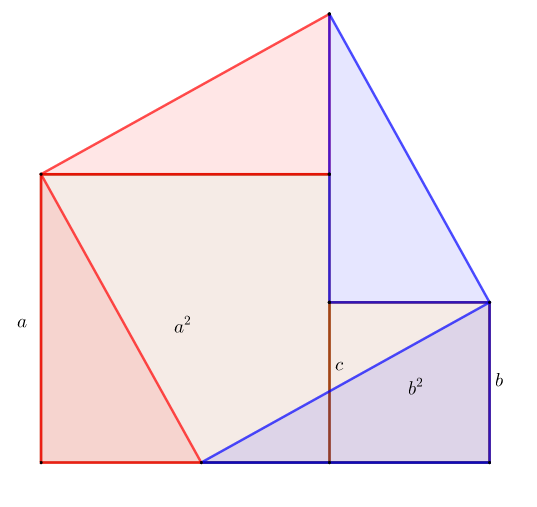
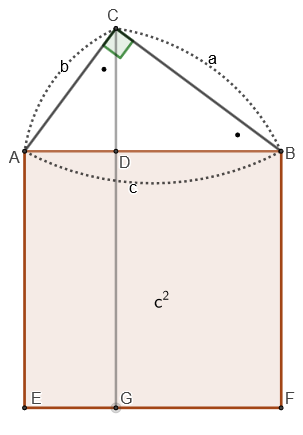
△ACD∼△CBD∼ABC
c:a=a:DB⇒a2=c×DB
c:b=b:AD⇒b2=c×AD
a2+b2=c×DB+c×AD=c×(DB+AD)=c2
이것은 1번 증명에서도 쉽게 알 수 있다.
AE×AD=b2,BF×BD=a2

아래와 같이 사다리꼴을 삼각형으로 잘라서 보일 수도 있다.

사다리꼴을 조금 다르게 써서 보일 수도 있다.
2b2=2×12×(b+a)×(b−a)+12×2c×c
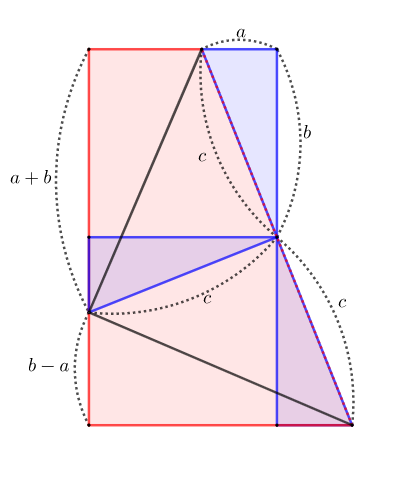
넓이의 비는 닮음비의 제곱과 같다.
닮음비 a:b:c이므로 넓이는 각각 ka2,kb2,kc2으로 놓을 수 있다.
kc2=ka2+kb2
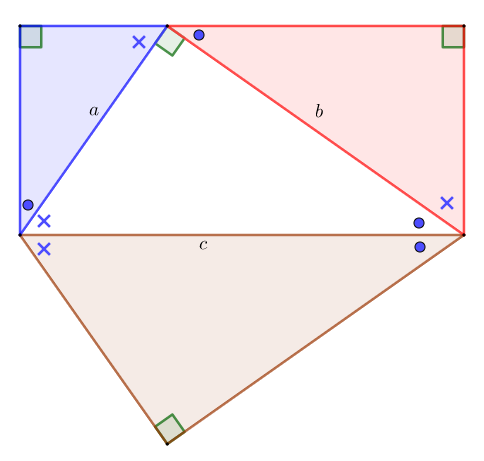
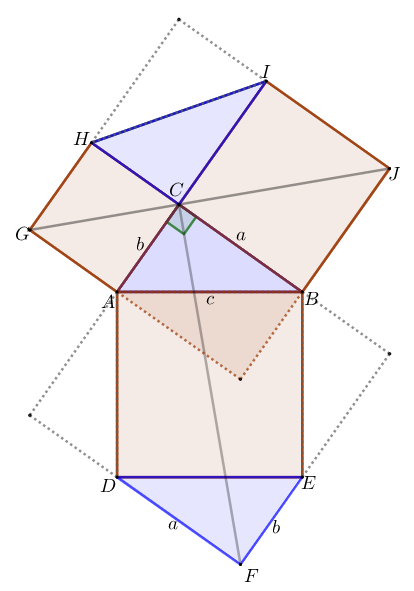
아래 그림에 있는 두 육각형 ABJIHG와 CADFEB는 넓이가 같다. 한 변이 a+b인 정사각형에서 △ABC와 같은 삼각형을 둘씩 잘라낸 다각형이기 때문이다.
넓이 (ABJIHG)= 넓이(CADFEB)
a2+b2+12ab=c2+12ab

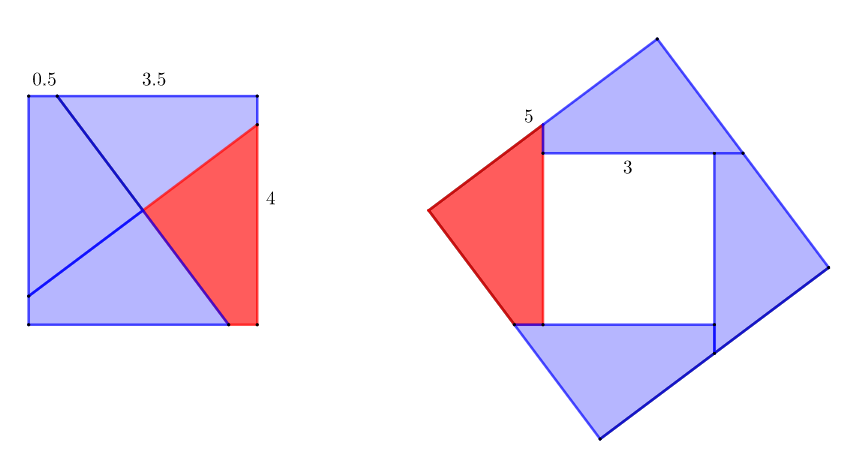
구장산술에는 구고현의 정리로 부르는 정리와 증명이 있다. 변의 길이가 3:4:5일 때를 보이고 있다.

왼쪽은 그림은 아래와 같이 색종이 오려 붙이기로 보일 수 있다.
Pythagorean Theorem and its many proofs
Pythagorean Theorem 'An exceedingly well-informed report,' said the General. 'You have given yourself the trouble to go into matters thoroughly, I see. That is one of the secrets of success in life.' Anthony Powell The Kindly Ones, p. 51 2nd Movement in A
www.cut-the-knot.org
피타고라스 정리를 퍼즐로 만든 상품이 많다. 조금 비싸긴 하지만 학교마다 다 사두고 있을 것이다. 수업 시간에 퍼즐을 해 보니 중학교 2학년에는 어려워하는 아이들이 보인다. 갑자기 하려고 하니 뚝딱 되지는 않는다. 나중을 위해서 답을 만들어 사진을 찍어둔다.








https://en.wikipedia.org/wiki/Pythagorean_theorem
Pythagorean theorem - Wikipedia
en.wikipedia.org
수학이야기님의
글이 좋았다면 응원을 보내주세요!