그림으로 증명하기
옛날 수학자들은 그림으로 증명하기를 꺼렸다. 엄밀함을 잃을 가능성이 있기 때문이다. 점, 선, 면 모두 이데아 속에 있는 것인데 눈에 보이는 그림으로 나타내면 왜곡이 있을 수 있다. 이제는 그림을 손이 아니라 컴퓨터로 그리기 때문에 상당히 정확하게 그릴 수 있다. 그만큼 왜곡된 그림으로 잘못된 결론에 도달할 가능성이 줄었다. 그림은 우리에게 직관하는 즐거움을 안겨주기도 한다. 몇 가지 예를 들어 보자.
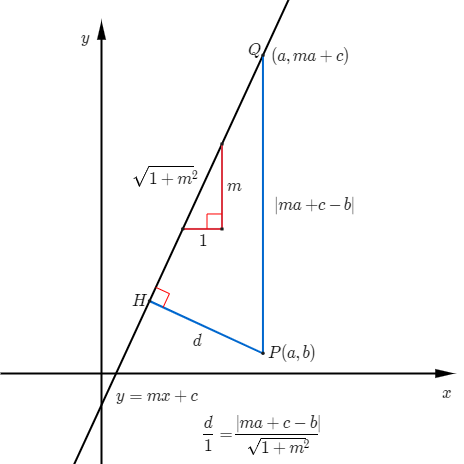
점과 직선 사이의 거리
점 $P$에서 직선 $y=mx+c$까지 거리 $d$를 구하는 방법을 설명하는 그림이다.
코사인 법칙
원의 성질로 증명
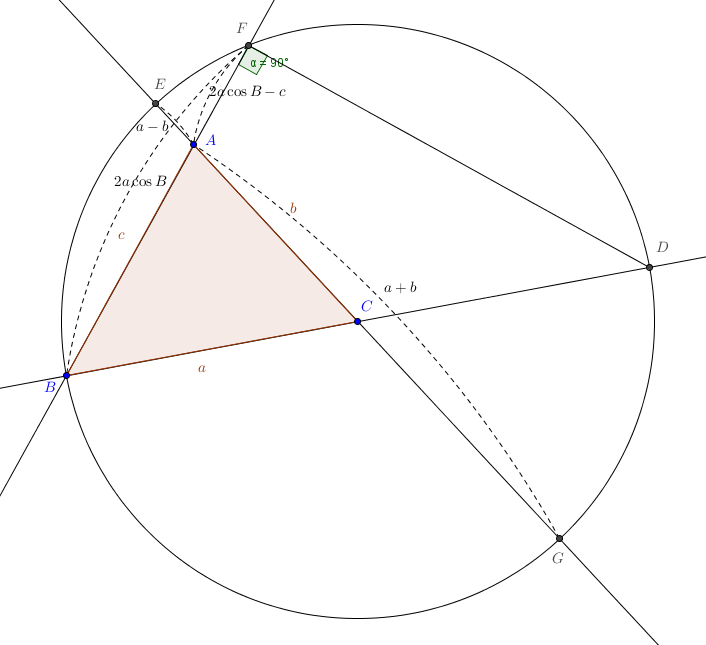
$$\overline{BA}\times \overline{AF}=\overline{EA}\times \overline{AG}$$
$$c(2a\cos B-c)=(a-b)(a+b)$$
$$c^2 =a^2 +b^2 -2ab\cos \theta$$
Timothy A. Sipka의 증명
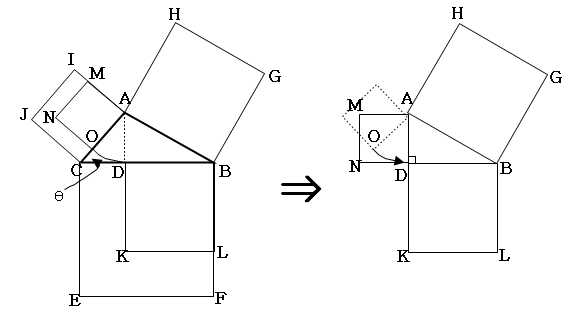
톨레미 정리로 증명
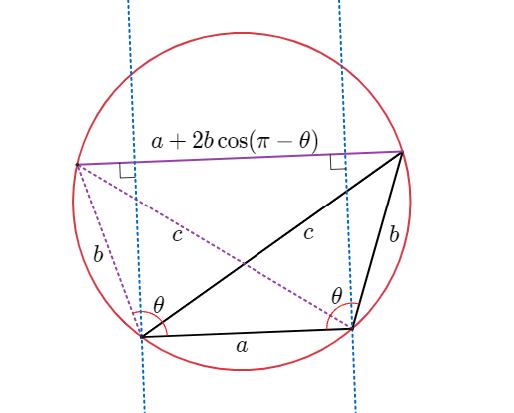
$$c\cdot c=b\cdot b+(a+2b\cos(\pi-\theta))\cdot a$$
$$c^2 =a^2 +b^2 -2ab\cos \theta$$
톨레미의 정리 - 수학노트
wiki.mathnt.net
수열의 합
자연수의 합
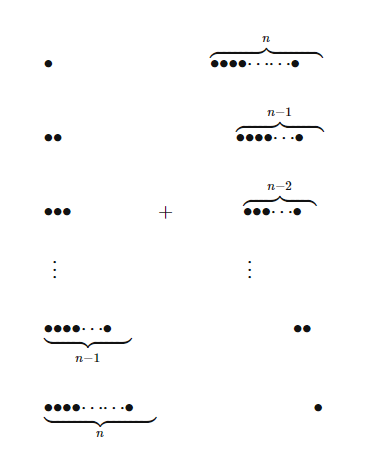
$$\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)$$
자연수 거듭제곱의 합
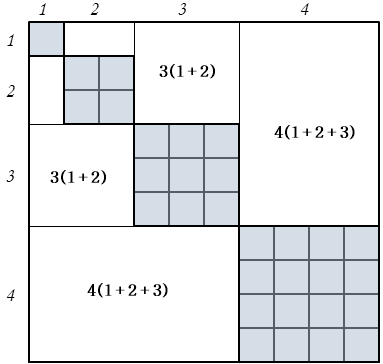
$$\begin{align}\sum_{k=1}^{n}k^2 &=\left(\sum_{k=1}^{n}k \right)^2- 2\sum_{k=1}^{n-1}\left[ \left(\sum_{i=1}^{k}i\right)(k+1)\right] \\&=\left(\sum_{k=1}^{n}k \right)^2-2\sum_{k=1}^{n-1}\frac{1}{2}k(k+1)(k+1)\\ &=\left(\sum_{k=1}^{n}k \right)^2-\sum_{k=1}^{n-1}(k^3 +2k^2+k)\\ &=\left(\sum_{k=1}^{n}k \right)^2-\sum_{k=1}^{n}(k^3 +2k^2+k)+n^3 +2n^2+n\\&=-2\sum_{k=1}^{n}k^2-\sum_{k=1}^{n}k+n^3+2n^2+n \end{align}$$
$$\begin{split}3\sum_{k=1}^{n}k^2&=-\frac{1}{2}n^2-\frac{1}{2}n+n^3+2n^2+n\\&=\frac{1}{2}n(2n^2+3n+n)\\&=\frac{1}{2}n(n+1)(2n+1)\end{split}$$
자연수 거듭제곱의 합
먼저 자연수의 합은 등차수열 합으로 간단히 적을 수 있다. 이를 그림으로 나타내면 아래와 같다. $$\sum _{k=1} ^{n} k =1 +2 +3 + \cdots +n = \frac{1}{2}n(n+1)$$ $\bullet$ $\overbrace{\bullet \bullet \bullet \bullet \cdots \
suhak.tistory.com
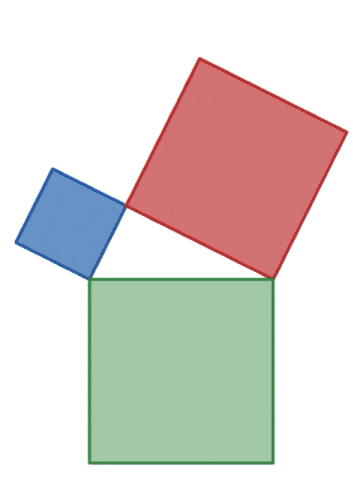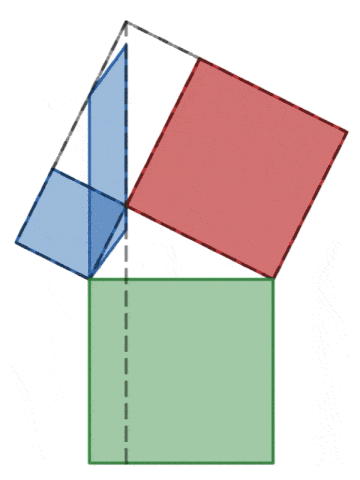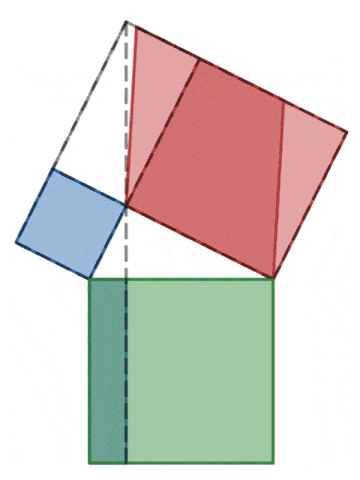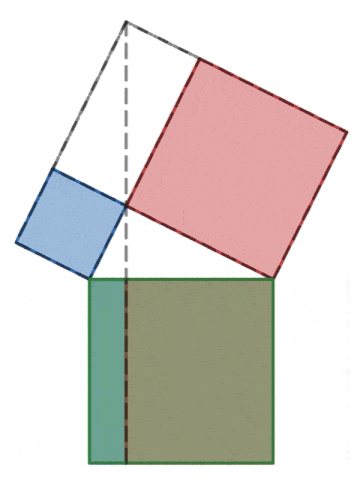
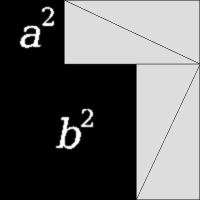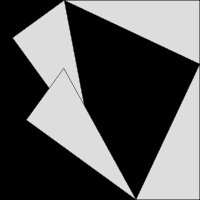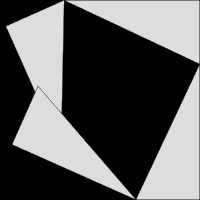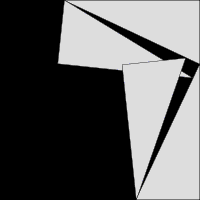
피타고라스 정리
 |
 |
피타고라스 정리의 증명을 몇 가지 알고 있나요?
피타고라스 정리는 유클리드 원론에 등장한다. 유클리드 원론에 있는 명제 47과 48은 아래와 같다. Proposition 47.In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the
suhak.tistory.com