나머지를 쉽고 빠르게 구하는 방법

수학을 전공한다면 대개 1학년 때 정수론(Number Theory)을 배우게 된다. 정수론은 수학을 공부할 때 반드시 거쳐야 하는 과목이다. 정수론의 세계도 얼핏 보기엔 쉽지만 마냥 쉽지만은 않다. 이 글은 정수론 맛보기를 위한 글이다.

정수론의 시작과 끝에는 소수가 있다. 소수는 중학교를 다녔다면 누구나 알고 있을 것이다.

소수(素數, prime number)는 한자로 '본디 소(素)'와 '셀 수(數)'를 쓰고 읽을 때는 '소쑤'이다. 소수는 1과 자기 자신만을 약수로 갖는 1보다 큰 자연수로 2, 3, 5, 7, 11,$\cdots$ 과 같은 수다. 한편,  0.1이나 2.4와 같은 소수(小數, decimal)는 '작을 소(小)'와 '셀 수(數)'를 쓴다.

소수는 무한하다. 당연히 끝을 알 수 없다. 에라토스테네스의 체라고 부르는 소수를 찾는 알고리즘이 있다. 이것도 중학교 1학년에서 배운다. 

1. 가장 작은 소수인 2를 남기고 모든 2의 배수를 지운다.

2. 다음 소수인 3을 남기고 모든 3의 배수를 지운다.

3. 4는 지워졌으므로 5를 남기고 모든 5의 배수를 지운다.

위와 같이 크기가 작은 소수를 찾고 그 소수의 배수를 지우는 알고리즘을 되풀이하면 된다.

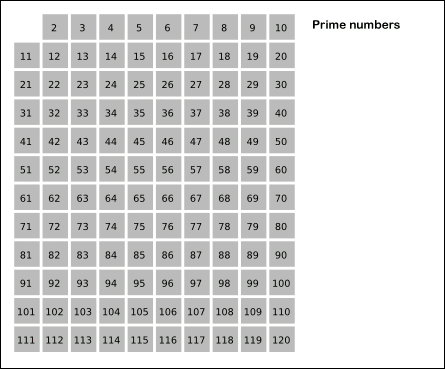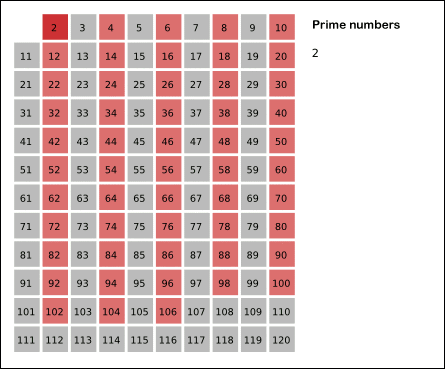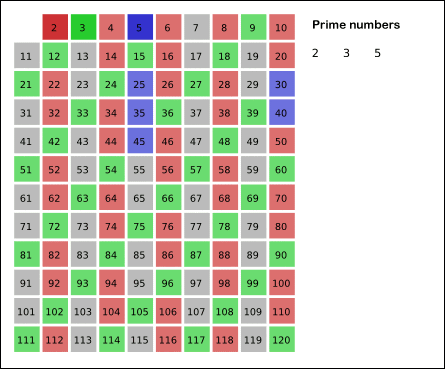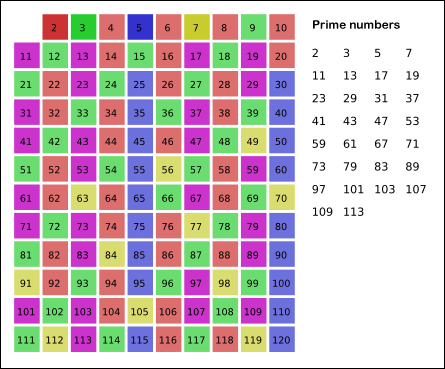
이 알고리즘을 컴퓨터 공학과에서 프로그래밍 연습 과제로 제시하는 모양이다. 여러 곳에서 눈에 띈다.

알고리즘에 따르면 주어진 수 $n$이 소수인가 판정하려면 $n/2$보다 작은 소수로 나누어 보아야 한다. 약수와 배수를 배우는 까닭이다.

배수판정법

주어진 수가 어떤 수의 배수인가를 판정할 때, 나눈 나머지가 0인가를 계산해야 한다. 주어진 수가 작을 때는 쉽지만 큰 수라면 쉽지 않다. 이때 아래와 같은 배수판정법을 알고 있다면 큰 도움이 된다.

$321,535,344$은 $m$의 배수인가?

$m$의 배수	판정법	$321,535,344$ 판정
2	일의 자리 수를 2로 나눈 나머지가 0	4는 2의 배수이므로 2의 배수
3	모든 자리 수의 합을 3으로 나눈 나머지가 0	3+2+1+5+3+5+3+4+4=30이므로 3의 배수
4	끝에서 두 자리 수를 4로 나눈 나머지가 0	44는 4의 배수이므로 4의 배수
5	일의 자리 수를 5로 나눈 나머지가 0	5로 나눈 나머지가 4이므로 5의 배수 아님
6	2의 배수이고 3의 배수	6의 배수
8	끝에서 세 자리 수를 8로 나눈 나머지가 0	344를 8로 나눈 나머지가 0이므로 8의 배수
9	모든 자리 수의 합을 9로 나눈 나머지가 0	자리 수 합은 30이므로 9의 배수가 아님
10	일의 자리 수가 0	10의 배수 아님

나머지가 같은 수를 나타내는 기호

$7^2$을 5로 나눈 나머지는 $49=5\times 9+4$이므로 $4$임을 쉽게 알 수 있다.

$7^4$을 $5$로 나눈 나머지는 얼마일까?

그나마 $7^4=49^2=(50-1)^2=2500-100+1=5(500-20)+1$이므로 나머지가 1임을 알 수 있지만 상당히 귀찮다.

하지만 $7^{41}$을 $5$로 나눈 나머지는 좀처럼 구하기 어렵다. 바로 이 순간이 수학이 필요한 순간이다. 나머지를 쉽게 다루기 위해서 나머지가 같은 것을 나타내는 새로운 기호를 하나 만들자.

두 자연수 $a,\,\,b$을 자연수 $m$으로 나눈 나머지가 같을 때, 아래와 같이 적는다. 
$$a\equiv b\quad \pmod{m}\tag{1}$$

참고: (1)에서 $a,b,m$을 정수로 바꿔도 문제없다. $m|(a-b)$로 써도 된다.(기호 $a|n$은 $a$는 $n$의 약수이다.)

읽을 때는 'a는 법 m에 대하여 b와 합동이다.'라고 읽는다. 영어로 법은 modular, 합동은 congruence이다. 'a is congruent to b modulo m' or 'a is congruent to b mod m'

자세한 것은 아래를 참고하자.

합동식

합동식의 몇 가지 성질을 보자.

' 두 수의 합이나 차를 나눈 나머지는 각각의 나머지의 합이나 차를 나눈 나머지와 같다.'

$a=mq_1+b$, $c=mq_2 +d$라고 하면 $$a\pm c=(mq_1 +b)\pm (mq_2+d)=m(q_1 \pm q_2)+b\pm d$$이다.

'두 수의 곱을 나눈 나머지는 나머지를 먼저 구하여 곱한 수를 나눈 나머지와 같다.' 

$a=mq_1+b$, $c=mq_2 +d$라고 하면 $$ac=(mq_1 +b)(mq_2+d)=m(mq_1q_2+q_2b+q_1d)+bd$$이다.

위를 합동식으로 나타내면 아래와 같다.

$$a\equiv b\pmod{m},\,\,c\equiv d \pmod{m}\Rightarrow a\pm c\equiv b\pm d\pmod{m}\tag{2}$$

 

$$a\equiv b\pmod{m},\,\,c\equiv d \pmod{m}\Rightarrow ac\equiv bd\pmod{m}\tag{3}$$

아래와 같은 성질도 쉽게 확인할 수 있다.

$$a\equiv b\pmod{m}\Rightarrow a^k\equiv b^k\pmod{m}\tag{4}$$

이제 $7^4$을 5로 나눈 나머지는 아래와 같이 구할 수 있다.

$$7^4\equiv 2^4 \equiv 1\pmod{5}$$

$7^{41}$을 5로 나눈 나머지도 가볍게 구할 수 있다.

$$7^{41}\equiv 2^{41} \equiv (2^4)^{10}\times 2\equiv 2\pmod{5}$$

배수판정법의 근거

이제 합동식으로 주어진 수를 $m$으로 나눈 나머지를 빠르게 구하는 방법을 알아보자. 우리는 수를 10진법으로 나타낸다. 예를 들면 아래와 같다.

$$12345=1\times 10^4+2\times 10^3 +3\times 10^2+4\times 10+5$$

밑이 10인 거듭제곱을 m으로 나눈 나머지를 먼저 구하면 편하다. 즉 법 m에 대한 합동식으로 생각하면 된다.

2의 배수와 5의 배수

$10\equiv 0 \pmod{2}$이므로 $10^k\equiv 0\pmod{2}$이다.

따라서 일의 자리가 2의 배수인 수는 모두 2의 배수이다.

$10\equiv 0 \pmod{5}$이므로 $10^k\equiv 0\pmod{5}$이다.

5의 배수는 2의 배수와 마찬가지로 일의 자리가 5의 배수인 수는 5의 배수이다.

3의 배수와 9의 배수

$10\equiv 1 \pmod{3}$이므로 $10^k\equiv 1\pmod{3}$이다.

따라서 $$\begin{align*}12345 &\equiv 1\times 10^4+2\times 10^3 +3\times 10^2+4\times 10+5\\ &\equiv 1+2+3+4+5\\ &\equiv 0 \pmod{3}\end{align*}$$

12345처럼 각 자리의 수를 더한 값이 3의 배수이면 3의 배수이다.

$10\equiv 1 \pmod{9}$이므로 $10^k\equiv 1\pmod{9}$이다.

9의 배수도 3의 배수와 마찬가지다.

4의 배수와 8의 배수

$10\equiv 2 \pmod{4}$이므로 $10^2\equiv 0\pmod{4}$이다. 따라서 $10^k \equiv 0 \pmod{4} (k \geq 2)$이므로 끝의 두 자리가 4의 배수인가 확인하면 된다.

$10\equiv 2 \pmod{8}$이므로 $10^3\equiv 0\pmod{8}$이다. 따라서 $10^k \equiv 0 \pmod{4} (k \geq 3)$이므로 끝의 세 자리가 8의 배수인가 확인하면 된다.

나머지가 음수

11의 배수

11의 배수를 판정하려면 나머지가 음수인 경우로 생각하면 된다.

$10=11\times 1+(-1)$로 생각하여 $10\equiv -1\pmod {11}$로 놓을 수 있다.

$k$가 홀수이면 $10^k\equiv -1\pmod {11}$, $k$가 짝수이면 $10^k\equiv \pmod {11}$이다.

11의 배수는 일의 자리부터 홀수 번째는 그대로 짝수 번째는 $-1$을 곱해서 더한 값을 11로 나누어서 확인할 수 있다.

$$\begin{align*}312345 &\equiv 3\times 10^5+1\times 10^4+2\times 10^3 +3\times 10^2+4\times 10+5\\ &\equiv -3+1-2+3-4+5\\ &\equiv 0\pmod{11}\end{align*}$$

$312345$는 11의 배수이다. 

참고: 도서를 분류하기 위한 ISBN 바코드의 체크 기호는 11로 나눈 나머지와 관련 있다.

7의 배수

마지막 7의 배수가 남았다. 이건 좀 복잡하다.

$10\equiv 3\pmod{7}$,

$10^2\equiv 3^2\equiv 2 \pmod{7}$,

$10^3\equiv 2\times 3\equiv 6\equiv -1\pmod{7}$

$10^6 \equiv 1\pmod{7}$

$$\begin{align*}312345 &\equiv 3\times 10^5+1\times 10^4+2\times 10^3 +3\times 10^2+4\times 10+5\\ &\equiv 10^3(3\times 10^2+1\times 10+2) +3\times 10^2+4\times 10+5\\ &\equiv -312+345\\ &\equiv 33\equiv 5 \pmod{7}\end{align*}$$

위와 같이 일의 자리부터 세 자리씩 끊어서 짝수 번째에 $-1$을 곱한 수를 더한 값을 구하여 확인한다.

$$-(3\times 2+1\times 3+2)+(3\times 2 +4\times 3+5)\equiv -11+23\equiv 5\pmod{7}$$

위와 같이 '일의 자리수$+$십의 자리수 $\times3+$백의 자리수$\times2$'로 계산하면 더 빠르다. 외우기 쉽게 세 자리씩 끊어서 생각하자.

$3214535344$를 7로 나눈 나머지는 얼마인가?

$$321535344\equiv 321-535+344 \equiv 130 \equiv 4\pmod{7}$$

이쯤에서 정수론 맛보기를 끝낸다. 뭔가 재미를 느꼈다면 수학을 잘할 자질을 갖춘 것이다. 짜증만 난다면 앞으로 수학 공부가 마냥 쉽지만은 않을 것이다.

거듭제곱은 복소수와 행렬에도 등장한다. 수학은 가장 간단한 원리로 가장 복잡한 문제를 해결할 수 있게 해주기때문에 아름답다. 이 글을 읽고 거듭제곱이 어려울 때 차수를 0부터 차근차근 올리며 일어나는 일을 살펴보면 된다는 사실을 새겨두면 좋겠다.