미분으로 할 수 있는 일 1

접선의 방정식

미분계수는 접선의 기울기이므로 먼저 접선을 구할 수 있다. 함수 $y=f(x)$ $x=a$에서 미분가능하다고 하자. 점 $(a,f(a)$에서 접선의 방정식은 아래와 같다.

$$y=f^{\prime}(a)(x-a)+f(a)$$ 함수 $y=\sin x$의 도함수는 $y^{\prime}=\cos x$이다. 따라서 $x=\pi$일 때 접선의 방정식은 $y=-x+\pi$이다.

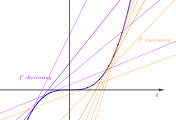
그림에서 보이듯이 $\varepsilon$이 충분히 작다면 $x=a$를 포함한 구간 $(a-\varepsilon, a+\varepsilon)$에서 두 함수의 그래프가 아주 비슷하다. 정리하면 곡선과 아주 비슷한 직선을 찾을 수 있으므로 미분으로 복잡한 함수를 간단한 1차 함수로 바꿔서 다룰 수 있게 된다.

함수의 증가와 감소

 

정의 1 어떤 구간 $I$에 있는 임의의 $x_1 ,\;\;x_2$에 대하여

$x_1<x_2$이면 $f(x_1)<f(x_2)$를 만족하면 이 구간에서 증가한다고 한다.

$x_1<x_2$이면 $f(x_1)>f(x_2)$를 만족하면 이 구간에서 감소한다고 한다.

 

정의 2 함수 $y=f(x)$의 정의역 $D$의 모든 $x$에 대하여 

$f(x)\leq f(c)$라면 이 함수는 $x=c$에서 최댓값(absolute maximum) $f(c)$를 가진다고 한다. 

$f(x)\geq f(c)$라면 이 함수는 $x=c$에서 최솟값(absolute minimum) $f(c)$를 가진다고 한다. 

 

정의 3 함수 $y=f(x)$에서 $f(c)$가 최댓값이 되는 정의역 $D$의 부분집합인 $c$를 포함하는 어떤 열린구간이 존재하면 $f(c)$는 극댓값(local maximum)이다. $f(c)$가 최솟값이 되는 구간이 존재한다면 극솟값(local minimum)이다. 이 값을 극값(local or relative extreme values)이라고 한다.

위에 있는 정의는 연속이나 미분가능성과 관계없이 정의한다. 함수가 연속이거나 미분가능하면 아래 정리가 성립한다.

정리 1 최대 최소 정리

닫힌구간 $[a,b]$에서 정의된 함수 $y=f(x)$는 주어진 구간에서 반드시 최댓값과 최솟값을 가진다. 다시 말해서 모든 $x$에 대하여 $f(x_1)=m\leq f(x)\leq M =f(x_2)$를 만족하는 $x_1 ,x_2\in[a,b]$가 존재한다.

이 정리는 증명이 어렵다. 해석학에서 실수의 완비성을 참고하자.

 정리 2 함수 $y=f(x)$의 정의역 $D$의 내부점 $c$에서 극값을 가지고 $x=c$에서 미분가능하면 $f^{\prime}(c)=0$이다.

증명

함수 $f$가 $x=c$에서 극댓값을 가진다고 하면 $c$에 충분히 가까운 $x$에 대하여 $f(x)-f(c)\leq 0$이다.

$x=c$에서 미분가능하므로 $$f^{\prime}(c)=\lim_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}$$가 존재한다.

$$f^{\prime}(c)=\lim_{x\rightarrow c+}\frac{f(x)-f(c)}{x-c} \leq 0\;\;(\because x-c>0)$$

$$f^{\prime}(c)=\lim_{x\rightarrow c-}\frac{f(x)-f(c)}{x-c} \geq 0\;\;(\because x-c<0)$$

$$\therefore\;\;f^{\prime}(c)=\lim_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}=0$$

극솟값을 가지는 경우도 마찬가지로 $f^{\prime}(c)=0$임을 증명할 수 있다.

 

정리 3 롤의 정리(Rolle's theorem)

함수 $y=f(x)$가 닫힌구간 $[a,b]$에서 연속이고 열린구간 $(a,b)$에서 미분가능하다고 하자. $f(a)=f(b)$라면 $f^{\prime}(c)=0$을 만족하는 $c$가 열린구간 $(a,b)$에 적어도 하나 존재한다.

증명

위에 있는 정리 1에 따라 연속인 함수 $f$는 닫힌구간 $[a,b]$에서 반드시 최댓값과 최솟값을 가진다.

1. $x=a$또는 $x=b$일 때 최댓값과 최솟값을 가진다면 함수 $f$는 상수함수이므로 $f^{\prime}(x)=0$이다. 따라서 구간에 있는 모든 $x$가 정리를 만족한다.

2. $a<c<b$인 $c$에서 최댓값 또는 최솟값을 가진다고 하자.

위에서 증명한 정리 2에 따라 $f^{\prime}(c)=0$이므로 정리를 만족한다.

 

이 정리를 일반화한 정리가 바로 평균값 정리다.

롤의 정리는 곡선 위에 있는 어떤 두 점을 잇는 직선이 $x$축과 평행하다면 반드시 수평인 접선horizontal tangent line이 존재함을 말한다. 

 정리 4 평균값 정리(Mean value theorem)

함수 $y=f(x)$가 닫힌구간 $[a,b]$에서 연속이고 열린구간 $(a,b)$에서 미분가능하다고 하자. 

$$f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}$$을 만족하는 $c$가 열린구간 $(a,b)$에 적어도 하나 존재한다.

 

증명

양 끝점 $(a,f(a)),(b,f(b))$를 지나는 직선의 방정식은 아래와 같다.

$$g(x)=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$$

$$h(x)=f(x)-g(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)$$

라고 하면 함수 $h$는 롤의 정리의 가정을 만족한다. 닫힌구간 $[a,b]$에서 연속이고 열린구간 $(a,b)$에서 미분가능하며  $h(a)=h(b)=0$이다.

따라서 $h^{\prime}(c)=0$인 $c$가 존재한다.

$$h^{\prime}(c)=f^{\prime}(c)-\frac{f(b)-f(a)}{b-a}=0$$

$$\therefore\;\;f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}$$

 

 

평균값 정리는 위 그림을 기억하면 쉽게 떠올릴 수 있다.

이 정리를 활용하면 함수의 증가와 감소를 미분계수로 쉽게 파악할 수 있다.

따름정리

함수 $f$가 닫힌구간 $[a,b]$에서 연속이고 열린구간 $(a,b)$에서 미분가능하다고 하자. 

1. $\forall x\in(a,b)\;\;f^{\prime}(x)>0$이면 함수 $f$는 구간 $[a,b]$에서 증가한다.

2. $\forall x\in(a,b)\;\;f^{\prime}(x)<0$이면 함수 $f$는 구간 $[a,b]$에서 감소한다.

증명

$x_1 ,x_2\in [a,b]$이고 $x_1 < x_2$ 라고 하자. 구간 $[x_1,x_2]$에서 평균값 정리에 따라

$$f(x_2)-f(x_1)=f^{\prime}(c)(x_2-x_1)$$인 $c$가 존재한다.

$x_2 -x_1 >0$이므로 $f^{\prime}(c)>0$이면 $f(x_1)<f(x_2)$이고, $f^{\prime}(c)<0$이면 $f(x_1)>f(x_2)$이다.

 

따름정리

1. 구간 $(a,b)$에 있는 모든 $x$에 대하여 $f^{\prime}(x)=0$이라면 함수 $\forall x \in (a,b)$에 대하여 $f(x)=C$인 상수함수이다.

2.  구간 $(a,b)$에 있는 모든 $x$에 대하여 $f^{\prime}(x)=g^{\prime}(x)$라면 $\forall x \in (a,b)$에 대하여 $f(x)=g(x)+C$인 상수가 존재한다.

증명 1 

$x_1 ,x_2\in [a,b]$이고 $x_1 < x_2$ 라고 하자. 구간 $[x_1,x_2]$에서 평균값 정리에 따라

$$f(x_2)-f(x_1)=f^{\prime}(c)(x_2-x_1)$$

이므로 $f(x_2)=f(x_1)$이다.

증명 2 $h(x)=f(x)-g(x)$라고 하면

$h^{\prime}(x)=f^{\prime}(x)-g^{\prime}(x)=0$이므로 따름정리 2도 성립한다.