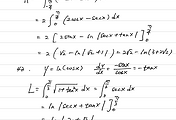$\int \sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)

치환적분은 여러 가지 어려운 문제를 해결해 준다. 그 가운데 삼각치환은 멋지다. 삼각치환을 넘어 쌍곡치환까지 정리해 둔다. 

$$\int \sqrt{1+x^2}dx$$

간단한 꼴이지만 풀려고 나서면 쉽지는 않다. 먼저 삼각치환을 써보자.

$$x=\tan\theta\quad\quad dx=\sec^2\theta d \theta$$

정리하면

$$\int \sqrt{1+\tan^2\theta}\sec^2\theta d \theta=\int \sec^3 \theta d\theta$$

결국 $I=\int \sec^3 \theta d\theta$의 부정적분을 찾아야 한다.

$$I=\int \sec \theta \cdot \sec^2 \theta  d\theta=\int \sec\theta \frac{d(\tan \theta)}{d\theta}d \theta$$

부분적분을 쓰자.

$$\begin{split}&=\sec\theta\tan\theta-\int \sec\theta\tan^2\theta d \theta\\&=\sec\theta\tan\theta-\int \sec\theta(\sec^2\theta -1)d \theta\\&=\sec\theta\tan\theta-\int \sec^3\theta d \theta+\int\sec\theta d \theta\\2I&=\sec\theta\tan\theta+\int\frac{\sec\theta(\sec\theta+\tan\theta)}{\sec\theta+\tan\theta} d \theta\\I&=\frac{1}{2}\sec\theta\tan\theta+\frac{1}{2}\ln{|\sec\theta+\tan\theta|} +C\end{split}$$

위에서 치환했던 변수를 되돌려 놓자.

$$\tan\theta=x,\quad\quad \sec\theta =\pm\sqrt{1+\tan^2 \theta}=\sqrt{1+x^2}$$

이므로 $\sec \theta>0$이라고 한다면

$$\int \sqrt{1+x^2}dx=\frac{1}{2}x\sqrt{1+x^2} +\frac{1}{2}\ln{|\sqrt{1+x^2}+x|} +C$$

이다. 생각보다 복잡하다.

참고로 $\int \sec^3 x dx$를 구하는 또 다른 방법도 있다.

$$\int \sec^3 x \, dx = \int \frac{dx}{\cos^3 x} = \int \frac{\cos x\,dx}{\cos^4 x} = \int \frac{\cos x\,dx}{(1-\sin^2 x)^2} = \int \frac{du}{(1-u^2)^2}$$

$$u = \sin x,\quad du = \cos x\,dx$$

$$\frac{1}{(1-u^2)^2} = \frac{1/4}{1-u} + \frac{1/4}{(1-u)^2} + \frac{1/4}{1+u} + \frac{1/4}{(1+u)^2}$$

$$=-\frac 1 4\ln (1-u) + \frac{1/4}{1-u} + \frac 1 4 \ln(1+u) - \frac{1/4}{1+u} + C$$

$$= \frac 1 4 \ln \frac{1+u}{1-u} + \frac 1 2 \frac{u}{1-u^2} + C$$

$$= \frac 1 4 \ln\frac{1+\sin x}{1-\sin x} + \frac 1 2 \frac{\sin x}{\cos^2 x} = \frac 1 4 \ln\frac{1+\sin x}{1-\sin x} + \frac 1 2 \sec x \tan x + C$$

 

다른 쉬운 방법은 없을까? 뜬금없어 보이지만 $$x=\frac{1}{2}(e^t -e^{-t})$$ 로 치환해 보자.

$$1+x^2 =1+ \frac{1}{4}(e^t -e^{-t})^2=\frac{1}{4}(e^t +e^{-t})^2,\quad dx=\frac{1}{2}(e^t +e^{-t})dt$$

이므로

$$\int \sqrt{1+x^2}dx=\int\frac{1}{4}(e^t +e^{-t})^2 dt=\frac{1}{4}\int(e^{2t} +e^{-2t}+2) dt$$

$$=\frac{1}{4}(\frac{1}{2}e^{2t}-\frac{1}{2}e^{-2t}+2t)+C=\frac{1}{8}(e^t -e^{-t})(e^t+e^{-t})+\frac{t}{2}+C$$

$2x=e^t -e^{-t}\quad e^{2t}-2x e^t -1=0$에서 $e^t =x+\sqrt{1+x^2}$이므로 $t=\ln|x+\sqrt{1+x^2}|$이다.

또한, $\displaystyle{x^2 +1= \frac{1}{4}(e^t +e^{-t})^2}$이므로 $\displaystyle{\frac{1}{2}(e^t+e^{-t})=\sqrt{1+x^2}}$이다.

다시 정리하면 삼각치환으로 했을 때와 같다. 지수함수를 적분하는 일이 매우 쉽기때문에 두 번째 치환이 훨씬 편하다. 이렇게 적분을 쉽게 해주는 치환을 생각하기 위해 아래와 같이 새로운 함수를 정의한다.

$$\sinh x=\frac{1}{2}(e^x -e^{-x}), \quad \cosh x =\frac{1}{2}(e^x +e^{-x})$$

이 함수가 쌍곡 함수인데 삼각함수와 매우 닮아서 이름도 비슷하게 붙였다. '하이퍼블릭 사인', '하이퍼볼릭 코사인'으로 읽는다. '신치 (/ˈsɪŋ, ˈsɪntʃ, ˈʃaɪn/) '와 '코시 (/ˈkɒʃ, ˈkoʊʃ/)'로 읽기도 한다. 하이퍼볼릭 우리말로 쌍곡선 $x^2 -y^2 =1$을 매개화한 것으로 생각하면 된다. 그림을 참고하자.

쌍곡선 $x^2 -y^2 =1$과 $x$축 그리고 원점을 지나는 직선으로 둘러싸인 붉은색 영역 넓이가 $a/2$일 때, 직선과 쌍곡선이 만나는 점을 $(\cosh a, \sinh a)$로 정의한다. 이것은 원 $x^2+y^2 =1$과 $x$축 그리고 원점을 지나는 직선으로 둘러싸인 부채꼴 넓이가 $\theta/2$일 때 직선과 원이 만나는 점을 $(\cos\theta, \sin\theta)$로 정의하는 것과 같다. 더 자세하게 알고 싶다면 아래 연결고리를 열어 보자.

hyperbolic_Function.ggb

다운로드

 

https://en.wikipedia.org/wiki/Hyperbolic_function