#9 1차 미분방정식(First-Order Differential Equations)

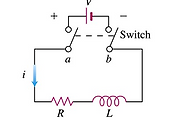
미리보기 우리가 실제로 만나는 많은 문제는 수학 공식으로 만들려 하면 미분방정식이 세워진다. 앞 선 단원에서 직선 위 운동, 인구 성장, 방사성 원소 붕괴, 낮은 온도의 매개체에 놓인 물체가 냉각되는 현상을 공부하였다. 4.8 단원에서 $dy/dx=f(x)$와 같은 꼴을 소개하였다. 함수 $f$가 연속인 구간이 있다면 바로 적분하여 $y=\int f(x)dx$ 일반해를 구할 수 있다. 다음으로 7.2 단원에서 $dy/dx=f(x,y)$과 같은 꼴인 미분방정식을 공부했다. 여기서 $x$는 독립변수이고 $y$는 종속변수이며 두 변수를 따로 떼어 놓을 수 있는 분리형(Separable) 문제를 배웠다. 9 장에서는 1차 미분방정식(일계 도함수만 포함된)이지만 조금 더 확장된 꼴을 공부한다. 간단한 전기 회로(RL circuit)나 화합물 혼합과 같은 문제를 다룬다.

9.1 해(Solutions), 기울기 장(Slope Field), 오일러 방법(Euler’s Method)

먼저 일계 도함수를 포함하고 있는 미분방정식을 정의한다. 다음으로 해를 기하적으로 보일 수 있는 기울기 장을 살펴본다. 많은 미분방정식은 해를 겉으로 드러난 양함수 꼴로 나타내기 어렵다. 그렇지만 수치 해석으로 해에 가까운 값을 구할 수 있다. 근삿값을 구하는 다른 여러 방법의 바탕이 되는 오일러 방법을 소개한다.

일반적인 1차 미분방정식과 해

1차 미분방정식은 다음 방정식과 같은 꼴이다. $$\frac{dy}{dx}=f(x,y)$$ $f(x,y)$는 $xy$평면에 표현할 수 있는 변수가 둘인 함수다. 일계 도함수(first derivative) $dy/dx$만 포함하고 있어서 1차(first-order)다. 다른 꼴로 다음과 같이 쓸 수 있는데 차이가 없는 같은 식이다. $$y^{\prime}=f(x,y)\quad \frac{d}{dx}y=f(x,y)$$ 어떤 구간 $I$에서 정의된 미분 가능한 함수 $y=y(x)$가 $$\frac{d}{dx}y(x)=f(x,y(x))$$ 와 같이 주어진 방정식을 만족하면 정의된 구간에서 방정식의 해가 된다. 즉, $y(x)$와 그 도함수 $y^{\prime}(x)$를 방정식에 대입하여 성립한다. 일반해(general solution) 는 가능한 모든 해를 포함하고 있다. 일반해는 항상 임의의 상수를 품고 있지만 상수를 가지고 있다고 모두 일반해인 것은 아니다. 어떤 해가 일반해가 되는 것을 밝히려면 미분방정식에 있는 깊은 내용이 필요하므로 더 심화된 책에서 배워야 한다. $y^{\prime}=f(x,y)$의 일반해 가운데서 $y(x_0)=y_0$를 만족하는 해를 찾으면 이 해는 특수해(particular solution)이다. 이와 같은 문제는 1차 초깃값 문제(first-order initial value problem)다.

기울기 장(slope field) : 곡선 해를 보이기 

초깃값 $y(x_0)=y_0$이 주어진 미분방정식을 만족하는 곡선 해는 $(x_0,y_0)$에서 접선 기울기는 $f(x_0,y_0)$가 된다. 미분방정식이 주어져 있으므로 선택한 점 $(x,y)$에서 기울기가 $f(x,y)$인 짧은 직선으로 나타낼 수 있다. 이 짧은 직선은 해가 되는 곡선 위 점에서 접선과 같다. 이렇게 그려진 그림을 기울기 장(방향 장 : direction field)으로 부른다. 이 그림에서 특수해를 그릴 수 있다.

기울기 장을 손으로 그리는 것은 엄청나게 지루한 일이다. 이 방법은 컴퓨터를 활용하는 것이 좋다,

오일러 방법(Euler’s Method)

미분방정식의 해를 쉽게 겉으로 드러나는 공식으로 구하기 어려울 때 컴퓨터를 써서 근삿값을 구할 수 있다. 해가 되는 곡선 위 점을 근삿값으로 구한 것을 수치 해(numerical solutions)라고 한다. 오일러 방법은 근삿값을 구하는 여러 가지 방법의 바탕이 되는 방법이다.

$$\frac{dy}{dx}=f(x,y)\quad y(x_0)=y_0$$

먼저 점 $(x_0,y_0)$에서 접선 기울기는 $f(x_0,y_0)$이므로 곡선을 접선으로 근사하면 된다.

$$L(x)=f(x_0,y_0)(x-x_0)+y_0$$

함수 $L(x)$는 $x_0$에 아주 가까운 구간에서는 매우 좋은 근삿값이 된다. 이제 충분히 작은 $dx$를 잡아서 다음 점을 찾는다.

$$x_1=x_0+dx\quad y_1=f(x_0,y_0)(x_1 -x_0)+y_0=f(x_0,y_0)dx+y_0$$

같은 방법을 되풀이하면 수치 해를 구할 수 있다.

$$x_2=x_1+dx\quad y_2=f(x_1,y_1)(x_2-x_1)+y_1=f(x_1,y_1)dx+y_1$$