만만하지 않은 상수 $\pi$와 $e$

수학 시간에 만나는 상수는 변수보다 만만하다. 그러나 깊이 들어가면 상수도 만만치 않다. 세상에 있는 많은 변수를 이해하려면 먼저 상수부터 알아야 한다. 아래 함수를 보면 생각나는 것이 있는가?

$$\phi(x)= \frac{1}{\sqrt{2\pi}}e ^ {-\frac{x^2}{2}}$$

표준정규분포의 확률밀도함수임을 알고 있다면 수학 공부 좀 한 사람이다. 세상에서 일어나는 많은 걸 분석할 수 있게 해주는 함수다. 신기하게도 이 함수에는 수학에서 자주 사용하는 두개의 상수 원주율 $\pi$와 오일러 상수 $e$가 함께 쓰였다. 세상을 알려면 먼저 원주율부터 공부해야 한다.

 

원주율 $\pi$

원주율 $\pi$는 지름(d)에 대한 원의 둘레(C)의 비율이다. $$\pi=\frac{C}{d}$$

원주율을 흔히 π라고 표시하는 이유는 그리스어로 둘레를 뜻하는 "페리페레스"(περιφηρής) 또는 "페리메트론"(περίμετρον)의 머리글자에서 따왔기 때문에 누가 처음 사용했는지 확실하지는 않으나 18세기 스위스의 수학자 ‘오일러(Leonhard Euler; 1707~1783)’가 쓰기 시작한 다음부터 다른 학자들도 이 표현을 따랐다고 한다.

$\pi$는 무리수이다. 근삿값은 $3.141592653589793238 \cdots$인데 고대 이집트 피라미드를 세운 사람은 $\displaystyle{2\pi=\frac{1760}{280} ≈ 6.2857}$로 계산했다고 하니 무척 정확하게 알고 있었다. 바깥 고리 위키백과

$\pi$는 이름도 무섭게 다가오는 초월수이기도 하다. 초월수는 어떤 대수 방정식의 답이 될 수 없는 수이다. 초월수는 작도할 수 없는 수이다. 따라서 원과 넓이가 같은 정사각형은 작도할 수 없다.

 

그리스 수학자 ‘아르키메데스(Archimedes; B. C. 287?-212)’는 원에 내접, 외접하는 다각형 둘레를 계산해 원주율은 $3$과 $\displaystyle{\frac{10}{71}}$ 보다는 크고, $3$과 $\displaystyle{\frac{1}{7}}$보다는 작다고 했는데 $\pi = 3.14\cdots$임을 밝힌 것이다. 영국 수학자 ‘샹크스(William Shanks; 1812-1882)’는 손으로 1873년경에 소수점 이하 $707$자리까지 원주율 값을 계산했지만, 안타깝게도 20세기 이후 소수점 이하 $528$자리까지는 맞고 그 뒤부터는 틀렸음이 밝혀졌다. 

아래와 같이 연분수로 나타낼 수 있다.

 

더 정확한 원주율을 찾기 위해선 미적분학이 필요하다. 15세기 인도 수학자 마드하반은 $\pi$의 값을 수렴하는 유리수의 무한급수로 나타낼 수 있음을 보였다. 1671년 스코틀랜드의 수학자 제임스 그레고리와 1674년 라이프니츠도 다시 찾아낸 식은 탄젠트의 역함수인 아크 탄젠트를 급수로 나타낸 식이다.

$$\begin{align}\arctan(z) &= z - \frac{z^3}{3} +\frac{z^5}{5} - \frac{z^7}{7} + \cdots \\&= \sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{2n+1} \, ; \qquad |z| \le 1 \qquad z \neq i,-i\end{align}\tag{1}$$

$\arctan (z)$에서 $z=1$일 때, 무한급수의 값은 $\pi/4$이다.

$$\pi=4\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{2k-1}=4(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots)$$

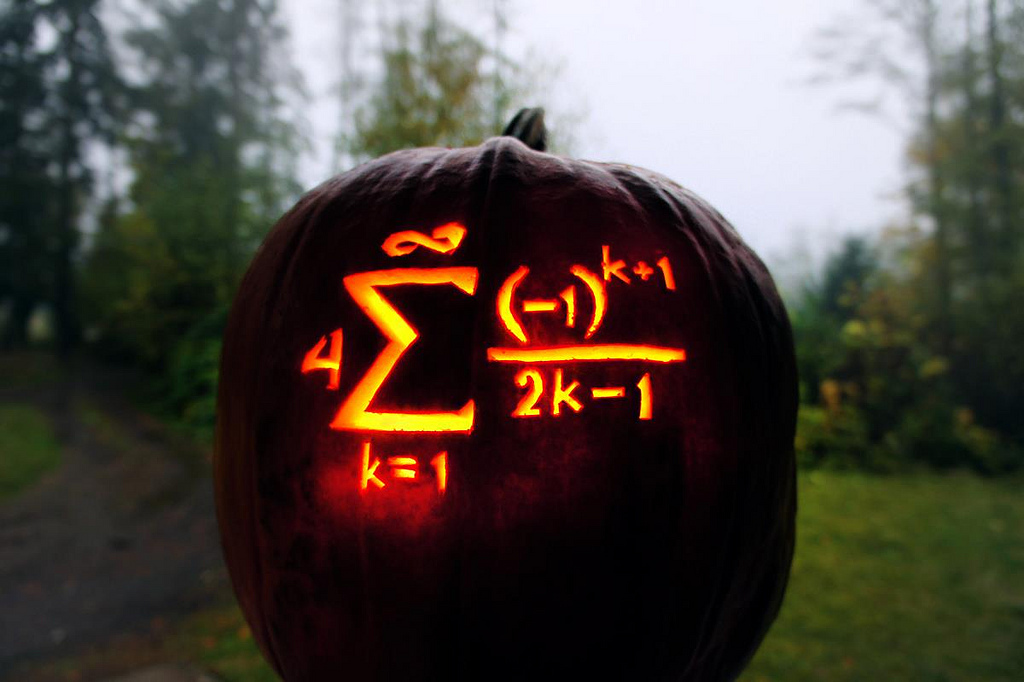
뉴턴은 아크 사인 함수를 나타내는 무한급수로 $\pi$의 근삿값을 찾았다. $\arcsin (z)$에서 $z=1$일 때, 무한급수의 값은 $\pi/2$이다.

$$\begin{align} \arcsin(z) & = z + \left( \frac{1}{2} \right) \frac{z^3}{3} + \left( \frac{1 \cdot 3}{2 \cdot 4} \right) \frac{z^5}{5} + \left( \frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6} \right) \frac{z^7}{7} + \cdots \\[5pt] & = \sum_{n=0}^\infty \frac{(2n-1)!!}{(2n)!!}\frac{z^{2n+1}}{2n+1} \\[5pt] & = \sum_{n=0}^\infty \frac{(2n)!}{(2^n n!)^2} \frac{z^{2n+1}}{2n+1} \, ; \qquad |z| \le 1 \end{align}\tag{2}$$

뉴턴은 1665년에서 1666년에 걸쳐 이 급수로 $\pi$의 값을 소수점 아래 열다섯 자리까지 구했다. 이 계산을 하는 동안은 다른 일을 하지 못했다고 한다.

요즘 슈퍼 컴퓨터의 성능은 무한급수로 $\pi$의 근삿값을 얼마나 빨리 구할 수 있는가로 측정한다고 한다.

한편  $\pi$는 무한곱으로 나타낼 수도 있다. 아래와 같은 월리스 곱이 그것이다.

$${\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)\\[6pt]&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \\\end{aligned}}}\tag{3}$$

오일러 상수 $e$

오일러 상수 $e$는 로그와 관계가 있다.

$e$가 계산된 최초의 기록은 1618년 존 네이피어가 발간한 로그표이다. 그러나 네이피어는 로그 계산 과정에서 나온 결과 값만을 간단히 다루었을 뿐 $e$를 상수로 취급하지는 않았다. 네이피어의 로그는 $N = 10^7 (1 - 10^{-7})^L $과 동치이다.

이를 오일러가 정의하여 오늘날까지 사용하고 있는 로그함수 정의로 옮기면 네이피어의 로그는

$$N = \log_n L \cdots \cdots n = ( 1- 10^{-7} )^{10^7} $$

인 로그함수이다. 위의 로그에서 사용된 밑은 $e$의 역수인 $\displaystyle{\frac{1}{e}}$와 매우 가까운 근삿값이다. 훗날 윌리엄 오트리드가 네이피어의 로그표를 사용하여 로그 계산자를 만들었지만 그 역시 $e$를 특별한 상수로 취급하지는 않았다.

$e$가 특정한 상수임을 발견한 사람은 자코브 베르누이다. 그는 복리 이자의 계산이 다음과 같은 극한을 취할 수 있다는 것을 발견하였다.

연이율이 100%라면 1년이 지나면 1원이 2원이 된다. 복리 이자 계산을 더 자주 한다면 원리합계는 어떻게 될까?  

$$\lim_{n\to\infty} (1+\frac{1}{n})^n $$

베르누이는 위 극한이 수렴한다는 것을 발견하였다. 물론 그 값은 $e$이다. 베르누이가 정리한 위의 급수를 처음으로 상수로서 표현한 사람은 고트프리트 빌헬름 라이프니츠이다. 라이프니츠는 1690년에서 1691년 사이에 크리스티안 하위헌스에게 쓴 편지에서 이 급수를 “b”로 표현하였다.

한편, 오일러는 1727년에서 1728년 사이에 이 상수를 $e$로 표현하여 사용하기 시작하였다. $e$라는 표기가 정식 출판물에 처음 등장한 것은 1736년 출판된 오일러의 《메카니카》이다. 그 이전에는 수학자마다 여러 알파벳을 사용하여 이 상수를 표기하였으나 《메카니카》의 출판 이후 $e$로 표기하는 것이 관례가 되었다. 오일러는 스위스 화폐에 등장한다. 우리나라 지폐에도 수학자가 등장할 날이 올까?