포락선(envelope)

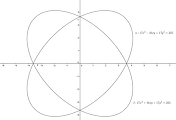
그림에서 파란 직선은 모두 $\displaystyle{\frac{x}{t}+\frac{y}{10-t}=1 \;\;(0<t<10)}$을 만족한다. 이 직선들을 직선무리 $C_t$로 놓을 때, 무리에 있는 직선마다 어떤 점에서 접하는 붉은 곡선을 이 직선무리의 포락선(envelope)으로 부른다. 일반적으로 미분 가능한 곡선은 모두 접선들로 이루어진 직선무리의 포락선이다.

$C_t$를 나타내는 방정식 $F_t (x,y)=0$을 $F(t,x,y)=0$으로 표현하면 포락선 위의 점 $P(x,y)$는 아래를 만족한다.

$$F(t,x,y)=\frac{\partial F(t,x,y)}{\partial t}=0$$

예를 들어 $\displaystyle{C_t : \frac{x}{t}+\frac{y}{1-t}=1}$라고 하자.

$$(1-t)x+ty-t(1-t)=t^2 +(-x+y-1)t +x=0$$이다.

$t$에 대하여 편미분하면 $2t+(-x+y-1)=0$이므로 $\displaystyle{t=\frac{x-y+1}{2}}$이므로 포락선은 아래를 만족한다.

$$\left(\frac{x-y+1}{2} \right)^2 +(-x+y-1)\frac{(x-y+1)}{2} +x=0$$

$$(-x+y-1)^2 -4x=0$$이다.

정리하면 $(x-y)^2 -2(x+y)+1=0$이다.

envelope.ggb

포락선으로 부르지만 일반화하면 평면일 수도 입체일 수도 있다. '포락'이란 말에서 뭔가 둘러싼다는 느낌이 오는가? 한자가 짧아서 그다지 느껴지지 않지만 영어말 'envelope'에선 느껴진다. 차라리 구글 번역처럼 '봉투'로 옮겨도 좋을 듯하다. '보자기'로 부르면 어떨까?^^

아무튼 포락선 놀이를 해보자. 원둘레에 있는 한 점과 원 안에 있는 한 점에서 같은 거리에 있는 직선무리를 생각해보자.

envelope_ellipse.ggb

원 $O$ 위의 점 $P$와 원 내부 점 $F$를 잇는 선분의 수직이등분선 무리를 $C_t$라고 하자. 점 $P$를 원 둘레로 회전하면 아래와 같이 타원이 포락선임을 알게 된다. 이차곡선의 정의를 안다면 증명은 간단하다.

envelope_parabola.ggb

타원과 같은 방법으로 초점을 원 밖에 두면 쌍곡선을 얻을 수 있다. 이를 활용하면 종이접기로 이차곡선을 찾아볼 수 있다.

아래 그림과 같이 원에 반사된 빛이 겹쳐지는 부분에 만들어지는 무늬인 화선(Caustics)도 포락선으로 생각할 수 있다.

잔에 담긴 커피에 빛을 비추면 아래 사진과 같이 사랑스러운 하트곡선이 나타난다.

소개팅 나가서 커피 마실 때 이야기해 보자. 결과가 좋다는 보장은 없다.

$$x=\cos\theta -\frac{1}{2}\cos\theta\cos 2\theta,\;\;y=\sin\theta-\frac{1}{2}\cos\theta \sin 2\theta$$