극좌표(Polar Coordinates)에서의 접선

1. 접선의 기울기

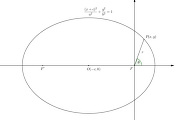
$P(r,\theta)$를 곡선 $C$ 위의 점이라 하고 곡선의 방정식을 $$r=f(\theta)$$라 하자.

점 $P$에서 기울기 $\tan \alpha$를 구해보자.

 

$$x=r\cos\theta,\;\;y=r\sin\theta$$

에서

$$\frac{dx}{d\theta}=r^{\prime}\cos\theta-r\sin\theta,\;\;\frac{dy}{d\theta}=r^{\prime}\sin\theta+r\cos\theta\;\bigg(r^{\prime}=\frac{dr}{d\theta}\bigg)$$

이다. 여기서 $\displaystyle{\frac{dx}{d\theta}\not=0}$이면 접선의 기울기는

$$\tan \alpha=\frac{dy}{dx}=\frac{r^{\prime}\sin\theta+r\cos\theta}{r^{\prime}\cos\theta-r\sin\theta} $$

$\displaystyle{\frac{dx}{d\theta}=0,\;\frac{dy}{d\theta}\not=0}$이면 접선은 $x$축과 수직이다. $\displaystyle{\frac{dx}{d\theta}=0,\;\frac{dy}{d\theta}=0}$인 점 $P$는 특이점(singular point)이라고 부른다.

문제 원 $r= 2\cos\theta$의 $\displaystyle{\theta=\frac{\pi}{4}}$에서의 접선의 기울기를 구하여라.

2. 동경벡터와 접선 사이의 각

이제 동경벡터 $\overrightarrow{OP}$와 접선이 이루는 각 $\varphi$라고 하고 이를 구해보자.

$r^{\prime},\cos\theta$가 모두 0이 아니라면 아래와 같이 바꿀 수 있다.

$$\tan \alpha=\frac{r^{\prime}\tan\theta+r}{r^{\prime}-r\tan\theta}$$

그림에서 $\varphi=\alpha-\theta$이므로

$$\tan\varphi=\tan(\alpha-\theta)=\frac{\tan\alpha-\tan\theta}{1+\tan\alpha\tan\theta}$$

대입하여 정리하면 아래와 같은 정리를 얻는다.

$$\tan\varphi=\frac{r}{r^{\prime}}$$

$\alpha<\theta$이면 $\varphi=\alpha+(\pi-\theta)=\alpha-\theta+\pi$이므로 같은 결과를 얻는다.

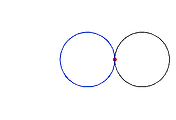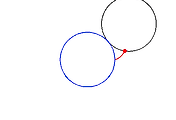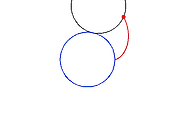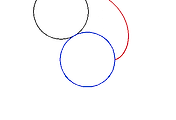
3. 두 곡선이 이루는 각

두 곡선 $C_0, C_1$이 점 $P$에서 만날 때 두 직선의 교각은 접선이 이루는 각으로 정의한다.

 

교각 $\phi=|\varphi_0 -\varphi_1|$이므로

$$\tan\phi=\bigg|\frac{\tan\varphi_0-\tan\varphi_1}{1+\tan\varphi_0\tan\varphi_1}\bigg|$$