5. Integration

고전 기하학에서 삼각형, 구, 원뿔의 넓이와 부피를 구한 것은 뛰어난 성취이다. 이제 더 일반적인 모양의 넓이와 부피를 구하는 방법을 살펴보자. 적분법(Integration)으로 부르는 이 방법은 더 많은 넓이와 부피를 구하는 도구이다. 적분(Integral)은 통계, 과학, 공학에서 중요한 기초다. 확률과 평균, 에너지 소비, 댐 수문에 미치는 힘과 같은 양을 계산하는데 쓴다. 여기에선 적분 개념이 곡선으로 둘러싸인 영역의 넓이를 구하는데 쓰임을 주로 살펴본다.

5.1 넓이와 유한합으로 추정하기 (Area and Estimating with Finite Sums)

수학, 과학에서 정적분(Definite integral)은 넓이, 부피, 곡선 길이, 확률, 무게와 같은 중요한 양을 계산하고 정하는 미적분의 중요한 도구다. 적분은 이런 값을 효과적으로 계산하기 위해 작은 조각으로 나누고 각 조각으로부터 구한 값을 합산하는 것이 기본 개념이다. 점점 더 많은 조각으로 점점 더 작은 조각으로 나눌 때 일어나는 일을 생각하자. 마침내 합에 쓰이는 부분의 개수가 무한히 커질 때 합의 극한을 다루는데 그 결과가 정적분이다.

정적분 공식의 기본은 알맞은 유한합(finite sum)을 구하는 데 있다. 일반적인 영역의 넓이와 닫힌 구간에서 함숫값의 평균을 엄밀하게 정의해야 하지만 먼저 직관적인 개념을 파악해야 한다. 따라서 유한합으로 근사하는 것에서부터 접근해 간다.

넓이(Area)

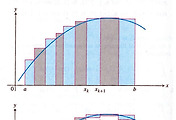
$y=1-x^2$의 그래프와 $x,y$축으로 둘러싸인 부분의 넓이를 찾아보자. 당연히 간단한 공식이 없다. 간단한 방식으로 근사시켜 보자.

 

 

구간 $[0,1]$을 등분하고 왼쪽 끝점에서의 함숫값을 세로로 등분된 구간을 가로로 하는 사각형의 넓이를 더한 값을 근삿값으로 생각하자. 이때 구해지는 값을 상합(upper sum)으로 부른다.

$$a) \quad A \approx 1\cdot \frac{1}{2}+\frac{3}{4}\cdot \frac{1}{2}=\frac{7}{8}=0.875$$

$$b) \quad A \approx 1\cdot \frac{1}{4} +\frac{15}{16}\cdot \frac{1}{4}+\frac{3}{4}\cdot \frac{1}{4}+\frac{7}{16}\cdot\frac{1}{4} =\frac{25}{32}=0.78125$$  

오른쪽 끝점에서 함숫값으로 계산하는 합은 하합(lower sum)으로 부른다.$$a) \quad A \approx \frac{15}{16}\cdot \frac{1}{4}+\frac{3}{4}\cdot \frac{1}{4}+\frac{7}{16}\cdot\frac{1}{4} +0\cdot\frac{1}{4}=\frac{17}{32}=0.53125$$  

아래와 같이 추정할 수 있다. $$0.53125<A<0.78125$$ 중간에 있는 점으로 근사할 수 있다.(midpoint rule)

$$b) \quad A \approx \frac{63}{64}\cdot \frac{1}{4}+\frac{55}{46}\cdot \frac{1}{4}+\frac{39}{64}\cdot\frac{1}{4} +\frac{15}{64}\cdot\frac{1}{4}=\frac{172}{64}\cdot\frac{1}{4}=0.671875$$  

일반화하면 구간 $[a,b]$를 $n$개의 부분구간(subinterval)로 등분했다고 하자. 구간 길이는 $\Delta x =(b-a)/n$이고 $c_k$는 $k$번 째 구간에 있는 점이라고 하면 아래와 같은 유한합을 생각할 수 있다.

$$f(c_1)\Delta x + f(c_2)\Delta x + f(c_3)\Delta x + \cdots +f(c_n)\Delta x $$

사각형을 점점 더 많이 만들면 사각형은 점점더 가늘어지고 부분구간의 길이가 거의 $0$에 가까워지면 근삿값은 점점 넓이 $A$에 가까워질 것이다. 이것을 넓이를 구하는 방법으로 삼는다.

이동거리(Distance Traveled)

방향을 바꾸지 않는 운동을 하는 물체의 속력이 $v(t)$로 주어졌다고 하자. 이때,

$$Distance=velocity\times time$$

이므로 이동거리 $D$는 아래와 같이 근삿값을 구할 수 있다.

$$D\approx v(t_1)\Delta t +v(t_2)\Delta t +\cdots +v(t_n)\Delta t$$

운동방향을 바꾸는 운동까지 생각하면 변위(displacement)와 이동거리(distance)를 구별해야 한다. 위에 주어진 식은 단지 위치의 차이인 변위를 나타내므로 속도가 아닌 속력(speed)로 계산한다.

$$D\approx |v(t_1)|\Delta t +|v(t_2)|\Delta t +\cdots +|v(t_n)|\Delta t$$

5.2 리만합 (Rieman Sums)

합의 기호 $\Sigma$를 써서 리만합을 정의하자.

먼저 구간 $[a,b]$에 $n-1$개의 점을 잡는다.

$$a<x_1 <x_2 <\cdots<x_{n-1}<b$$

$$a=x_0<x_1 <x_2 <\cdots<x_{n-1}<x_n =b$$

 

이때 집합 $P=\{x_0 ,x_1, x_2, \cdots ,x_{n-1}, x_n \}$을 구간 $[a,b]$의 분할(partition)이라고 부른다. 분할 $P$의 $k$번 째 부분구간은 $[x_{k-1},x_k]\quad k=1,2,\cdots n$각각의 부분구간의 길이를 $\Delta x_k=x_k-x_{k-1}$로 나타낸다. 구간의 길이가 같을 필요는 없다. 이제 $c_k \in [x_{k-1},x_k]$라고 하고 얻어지는 아래와 같은 부분합 $S_p$를 리만합이라고 한다.

$$S_P=\sum_{k=1}^{n}f(c_k)\Delta x_k$$

분할 $P$에서 가장 긴 구간의 길이를 크기(norm)로 정의하고 $||P||$로 적는다.

 

5.3 정적분 (Definite Integral)

Definition Let $f(x)$ be a function defined on a closed interval $[a,b]$. We say that a number $J$ is the definite integral of $f$ over $[a,b]$ and that $J$ is the limit of the Riemann sums $\displaystyle{\sum_{k=1}^{n}f(c_k)\Delta x_k}$ if the following condition is satisfied :

Given any number $\epsilon>0$ there is a corresponding number $\delta>0$ such that for every partition $P=\{x_0 ,x_1, x_2, \cdots ,x_{n-1}, x_n \}$ of $[a,b]$ with $||P||<\delta$ and any choice of $c_k\in[x_{k-1},x_k]$, we have

$$\left|\sum_{k=1}^{n}f(c_k)\Delta x_k-J\right|<\epsilon$$