6. Applications of Definite Integrals

 정적분을 활용하여 부피, 곡선길이, 회전체의 표면적을 구해보자.

부피(Volume)

부피도 넓이와 마찬가지로 먼저 리만합으로 근삿값을 구하고 이 합의 극한값으로 정의한다고 이해하자.

1. 평행한 판으로 자르기(Slicing by Parallel Planes)



 

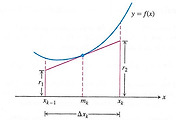
그림에서와 같이 먼저 구간 $[a,b]$를 분할하자.

$$a=x_0 <x_1 <x_2 <\cdots<x_n =b$$

$x_k$를 지나고 $x$축에 수직인 평면을 $P_k$라고 하자.

평행한 평면 $P_k$로 입체를 자른다고 하자.

$k$번 째 부분구간에서 만들어지는 판(slab)은 밑면이 넓이가 $A(x_k)$이고 높이가 $\Delta x_k=x_{k}-x_{k-1}$인 기둥과 비슷한 부피를 가진다고 생각하면 근삿값을 아래와 같이 적을 수 있다.

$$V_k=A(x_k)\Delta x_k$$

전체 부피는 아래와 같은 유한합으로 근사할 수 있다.

$$V\approx \sum_{k=1}^{n}V_k =\sum_{k=1}^{n}A(x_k)\Delta x_k$$

앞에서 리만합의 극한값으로 정적분을 정의하였다.

그러므로

$||P||\rightarrow 0$일 때, 극한을 생각하면

$$\lim_{n\rightarrow \infty}\sum_{k=1}^{n}A(x_k)\Delta x_k=\int_{a}^{b} A(x)dx$$

따라서 아래와 같이 정의한다.

Definition

The volume of a solid of integrable cross-sectional area $A(x)$ from $x=a$ to $x=b$ is the integral of $A$ from $a$ to $b$,

$$V=\int_{a}^{b} A(x)dx$$



보기 1. 높이가 3이고 밑면은 한 변이 3인 정사각형인 피라미드의 부피를 구하여라.

풀이 ))

꼭짓점을 원점으로 하고 높이를 $x$축으로 놓는다.

점 $x$를 지나고 $x$축에 수직인 평면으로 잘린 단면의 넓이는 $x^2$이다.

따라서 $V=\int_{0}^{3}x^2 dx=9$이다.

 

보기 2. 밑면의 반지름이 3인 원기둥을 그림과 같이 지름을 지나고 밑면과 이루는 각이 $45^{\circ}$인 평면으로 자를 때 생기는 쐐기 모양의 부피를 구하여라.

풀이))

그림과 같이 축을 설정하면

$$A(x)=height \times width=(x)(2\sqrt{9-x^2})$$

$$V=\int_{0}^{3}2x\sqrt{9-x^2} dx=18$$

 

 

2. 회전체의 부피(Solid of Revolution: The Disk Method)

축을 둘레로 회전한 입체의 부피는 아래와 같이 구할 수 있다.

$$V=\int_{a}^{b} A(x)dx=\int_{a}^{b} \pi [R(x)]^2 dx$$

$$V=\int_{c}^{d} A(y)dy=\int_{c}^{d} \pi [R(y)]^2 dy$$

3. 회전체의 부피(Solid of Revolution: The Washer Method)

두 곡선으로 둘러싸인 부분을 축을 둘레로 회전한 입체의 부피는 아래와 같이 구할 수 있다.



$$V=\int_{a}^{b} A(x)dx=\int_{a}^{b} \pi ([R(x)]^2 -[r(x)]^2)dx$$

 



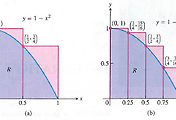
보기 3. 곡선 $y=x^2 +1$과 직선 $y=-x+3$으로 둘러싸인 부분을 $x$축을 둘레로 회전하였을 때 생기는 입체의 부피를 구하여라.

풀이))

그림 (a)를 참고하자.

바깥쪽 반지름은 $R(x)=-x+3$

안쪽 반지름은 $r(x)=x^2 +1$

그림 (b) 나타난 얇은 판은 볼트와 너트 사이에 끼워 풀리는 것을 막아주는 와셔를 닮았다.

위, 아래끝(Limit of integration)을 찾기 위하여 곡선과 직선이 만나는 점을 찾으면

$$-x+3=x^2 +1$$

$$x^2 +x-2=0$$

$$x=-2,\quad x= 1$$

이다.

$$V=\int_{a}^{b} A(x)dx=\int_{a}^{b} \pi ([R(x)]^2 -[r(x)]^2)dx$$

$$=\int_{-2}^{1} A(x)dx=\int_{a}^{b} \pi ([-x+3]^2 -[x^2 +1]^2)dx$$

$$=\int_{-2}^{1} A(x)dx=\int_{a}^{b} \pi (8-6x-x^2 -x^4)dx$$

$$=\pi\big[8x-3x^2 -\frac{x^3}{3}-\frac{x^5}{5}\big]_{-2}^{1}=\frac{117 \pi}{5}$$

 

4. 원기둥 껍질로 구하는 부피(Solid of Revolution: Cylindrical Shells)

$x$축과 포물선 $f(x)=3x-x^2$으로 둘러싸인 부분을 $x=-1$을 축으로 회전하여 만드는 입체의 부피를 구해보자.

이 경우도 $x$축 방향으로 $1$만큼 평행이동하여 와셔법을 쓸 수도 있다. 하지만 계산이 매우 복잡해진다. 따라서 새로운 방법을 고안할 필요가 있다. 두께가 $\Delta y$인 수평 띠가 아니라 두께가 $\Delta x$인 수직 띠를 회전한 것으로 생각하는 것이다. 와셔가 아니라 원기둥이 생기므로 원기둥 껍질법으로 부르자.

 

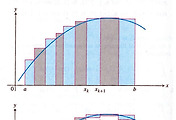
먼저 구간 $[0,3]$을 분할하자.

그림과 같은 원기둥은 두께가 $\Delta x_k$, 높이는 $y_k$, 반지름은 $1+x_k$이다. 따라서 $k$번 째 구간에서 만들어지는 입체의 부피는

$$V_k=2\pi(1+x_k)\cdot(3x_k -{x_{k}}^2)\Delta x_k$$

이다.

이 부피를 더하면 근삿값을 얻는다. $$V\approx \sum_{k=1}^{n}V_k =\sum_{k=1}^{n}2\pi(1+x_k)\cdot(3x_k -{x_{k}}^2)\Delta x_k$$ 마찬가지로 $||P||\rightarrow 0$일 때, 극한을 생각하면 정적분의 정의에 따라 부피를 구할 수 있다.

$$V=\lim_{n\rightarrow \infty}\sum_{k=1}^{n}2\pi(1+x_k)\cdot(3x_k -{x_{k}}^2)\Delta x_k$$

$$=\int_{0}^{3} 2\pi(x+1)(3x-x^2)dx=\frac{45\pi}{2}$$

Shell Formula for Revolution About a Vertical Line

The volume of the solid generated by revolving the region between the x-axis and the graph of a continuous function $y=f(x) \geq 0, \;\;L\leq a \leq b$, about a vertical line $x=L$ is

$$V=\int_{a}^{b} 2\pi (x-L)f(x)dx$$

$$V=\int_{a}^{b} 2\pi (shell\;\;radius)(shell\;\; height)dx$$

 

호 길이(Arc Length)

$x=a$에서 $x=b$까지 곡선 $y=f(x)$의 길이를 구해보자.

 

먼저 구간 $[a,b]$의 분할 $P$를 생각하자.

$$a=x_0 <x_1<x_2<\cdots<x_n=b$$ 

$y_k =f(x_k)$라면 점 $P_k (x_k ,y_k )$는 곡선 위에 있다. 곡선 길이의 근삿값은 다각형 경로로 구할 수 있다.

$\Delta x_k=x_k -x_{k-1}, \Delta y_k=y_k -y_{k-1}$라고 하면

$$L_k=\sqrt{(\Delta x_k )^2 +(\Delta y_k)^2}$$

호 길이를 $L$이라고 하면

$$L\approx\sum_{k=1}^{n}L_k=\sum_{k=1}^{n}\sqrt{(\Delta x_k)^2 +(\Delta y_k)^2}$$

이다. 평균값에 정리에 의해 구간 $[x_{k-1},x_k]$에 아래를 만족하는 $c_k$가 존재한다.

$$\Delta y_k =f^{\prime}(c_k)\Delta x_k$$

따라서,

$$\sum_{k=1}^{n}L_k=\sum_{k=1}^{n}\sqrt{ 1 +[f^{\prime}(c_k)]^2}\sqrt{ (\Delta x_k )^2}=\sum_{k=1}^{n}\sqrt{ 1 +[f^{\prime}(c_k)]^2}\Delta x_k $$

정적분 정의에 따라 아래와 같이 곡선 길이를 정의한다.

$$L=\lim_{n\rightarrow \infty}\sum_{k=1}^{n}\sqrt{ 1 +[f^{\prime}(c_k)]^2}\Delta x_k=\int_{a}^{b}\sqrt{1+[f^{\prime}(x)]^2}dx$$

다시 적으면

구간 $[a,b]$에서 연속인 곡선 $y=f(x)$ 길이(호 길이)는

$$L=\int_{a}^{b}\sqrt{1+[f^{\prime}(x)]^2}dx=\int_{a}^{b}\sqrt{1+\bigg(\frac{dy}{dx}\bigg)^2}dx$$

$y=f(x)$와 $ f^{\prime}$이 $[a,b]$에서 연속이라면 미적분의 기본정리에 따라 아래와 같은 새로운 함수를 정의할 수 있다.

$$s(x)=\int_{a}^{x}\sqrt{1+[f^{\prime}(t)]^2}dt$$

이 함수를 호 길이 함수(Arc length function)으로 부른다.

$$\frac{ds}{dx}=\sqrt{1+[f^{\prime}(x)]^2}=\sqrt{1+\bigg(\frac{dy}{dx}\bigg)^2}$$

$$ds=\sqrt{1+\bigg(\frac{dy}{dx}\bigg)^2}dx$$

$$ds=\sqrt{dx^2 +dy^2}$$

이 식을 활용하면 많은 공식을 간단하게 표현할 수 있다.

회전체의 겉넓이(Areas of Surfaces of Revolution)

아래와 같이 원뿔대의 겉넓이는 펼친 그림으로 구한다.

이 개념을 정적분으로 일반화하면 회전체의 겉넓이도 정의할 수 있다.

그림에서 곡선 $PQ$가 쓸고 지나간 부분의 넓이는 선분 $PQ$가 쓸고 지나간 부분인 원뿔대의 겉넓이로 근삿값을 구할 수 있다. 위 그림에서 $2\pi y^* L$이다. 여기서 $y^*$는 선분 $PQ$ 높이의 평균이다.

$$y^* =\frac{f(x_{k-1})+f(x_k)}{2},\quad L=\sqrt{(\Delta x_k )^2 +(\Delta y_k )^2}$$

$$\therefore Frustum\;\;surfaces\;\;area=2\pi\cdot \frac{f(x_{k-1})+f(x_k)}{2}\cdot\sqrt{(\Delta x_k )^2 +(\Delta y_k )^2}$$

$$S\approx\sum_{k=1}^{n}\pi\big(f(x_{k-1})+f(x_k)\big)\sqrt{(\Delta x_k )^2 +(\Delta y_k )^2}$$

 

 

곡선의 길이와 마찬가지로 평균값 정리에 따라 구간 $[x_{k-1},x_k]$에 아래를 만족하는 $c_k$가 존재한다.

$$\Delta y_k =f^{\prime}(c_k)\Delta x_k$$

$$S\approx\sum_{k=1}^{n}\pi\big(f(x_{k-1})+f(x_k)\big)\sqrt{(\Delta x_k )^2 +(f^{\prime}(c_k)\Delta x_k )^2}$$

$$S\approx\sum_{k=1}^{n}\pi\big(f(x_{k-1})+f(x_k)\big)\sqrt{1 +(f^{\prime}(c_k) )^2}\Delta x_k $$

위에 있는 합은 리만합은 아니지만 $||P||\rightarrow0$라면 주어진 합은 아래와 같은 정적분으로 수렴한다.

$$\int_{a}^{b}2\pi f(x)\sqrt{1+(f^{\prime}(x))^2}dx$$

Definition

If the function $f(x)\geq 0$ is continuously differentiable on $[a,b]$, the area of the surfaces generated by revolving the graph $y=f(x)$ about the x-axis is

$$S=\int_{a}^{b}2\pi y\sqrt{1+\bigg(\frac{dy}{dx}\bigg)^2}dx=\int_{a}^{b}2\pi f(x)\sqrt{1+(f^{\prime}(x))^2}dx$$