2017학년도 카이스트 일반전형 수학문제
수학이야기/면접논술 2016. 11. 29. 13:20좌표평면 위의 점 $(a,0),(0,9-a)$를 잇는 모든 선분의 집합을 $D$라고 하자. 아래 물음에 답하여라.($0\leq a \leq 9$)
1) 선분이 점 $(1,4)$를 지나게 하는 모든 $a$의 값을 구하여라.
2) $D$가 점 $(1,y)$를 지날 때 $y$의 최댓값을 구하여라.
3) $D$의 모든 선분이 그리는 도형의 넓이를 구하여라.
풀이 $x,y$ 절편이 각각 $(a,0),(0,9-a)$인 직선의 방정식은
$$\frac{x}{a}+\frac{y}{9-a}=1$$
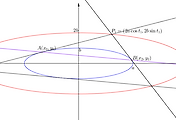
이다. 그림으로 나타내면 집합 $D$는 위 그림에서 1사분면에 있는 영역이다.
먼저 1)에서 점 $(1,4)$를 지난다고 하면
$$\frac{1}{a}+\frac{4}{9-a}=1$$
$$9-a+4a=a(9-a)$$
$$a^2 -6a+9=0\quad \therefore a=3$$
2)에서 점 $(1,y)$를 지난다고 하면
$$\frac{1}{a}+\frac{y}{9-a}=1$$
$$9-a+ya=a(9-a)$$
$$y= 9-a +\frac{a-9}{a}=10-a-\frac{9}{a}=10-\bigg(a+\frac{9}{a}\bigg) \leq 10-2\sqrt{a\times \frac{9}{a}}=4$$
3) 그림에서 집합 $D$가 그리는 영역의 윗쪽 경계는 $x=t$일 때 $y$의 최댓값을 구하면 알 수 있다.
$$\frac{t}{a}+\frac{y}{9-a}=1$$
$$t(9-a)+ya=a(9-a)$$
$$y= 9-a +\frac{t(a-9)}{a}=9+t-\bigg(a+\frac{9t}{a}\bigg) \leq 9+t-2\sqrt{a\times \frac{9t}{a}}$$
그러므로 경계는
$$y=9+x-6\sqrt{x}\;\;(0\leq x \leq 9)$$
이다. 그러므로 영역의 넓이 $S$를 구하면 아래와 같다.
$$S=\int_{0}^{9}(9+x-6\sqrt{x})dx=\bigg[ 9x+\frac{1}{2}x^2 -4x\sqrt{x}\bigg]_{0}^{9}=\frac{27}{2}$$
이 문제는 포락선(envelope) 문제로 해석할 수도 있다. 더 어렵게 느껴지지만 포락선 문제로 풀어보자.
그림에서 집합 $D$를 이루는 직선은 모두 $\displaystyle{\frac{x}{t}+\frac{y}{9-t}=1 \;\;(0<t<9)}$을 만족한다. 이 직선들을 직선무리 $C_t$로 놓을 때, 무리에 있는 직선마다 어떤 점에서 접하는 곡선을 이 직선무리의 포락선(envelope)으로 부른다. 일반적으로 미분 가능한 곡선은 모두 접선들로 이루어진 직선무리의 포락선이다.
$C_t$를 나타내는 방정식 $F_t (x,y)=0$을 $F(t,x,y)=0$으로 표현하면 포락선 위의 점 $P(x,y)$는 아래를 만족한다.
$$F(t,x,y)=\frac{\partial F(t,x,y)}{\partial t}=0$$
예를 들어 $\displaystyle{C_t : \frac{x}{t}+\frac{y}{1-t}=1}$라고 하자.
$$(1-t)x+ty-t(1-t)=t^2 +(-x+y-1)t +x=0$$이다.
$t$에 대하여 편미분하면 $2t+(-x+y-1)=0$이므로 $\displaystyle{t=\frac{x-y+1}{2}}$이므로 포락선은 아래를 만족한다.
$$\left(\frac{x-y+1}{2} \right)^2 +(-x+y-1)\frac{(x-y+1)}{2} +x=0$$
$$(-x+y-1)^2 -4x=0$$이다.
정리하면 $(x-y)^2 -2(x+y)+1=0$이다.
이 곡선을 원점을 중심으로 $\pi/4$ 회전하자.
$$\pmatrix{x^{\prime}\\y^{\prime}}= \frac{1}{\sqrt{2}} \pmatrix{1 &-1\\1 &1}\pmatrix{x\\y}$$
$$x-y=\sqrt2 x^{\prime},\;\;x+y=\sqrt2 y^{\prime}$$
$$y^{\prime}=\frac{\sqrt2}{2}(x^{\prime})^2 +\frac{\sqrt 2}{4}$$
로 포물선임을 알 수 있다.
주어진 문제를 같은 방식으로 풀면 아래와 같은 곡선을 얻을 수 있다.
$$\displaystyle{\frac{x}{a}+\frac{y}{9-a}=1 \;\;(0<a<9)}$$
$$F(a,x,y)=(9-a)x+ay-a(9-a)=a^2 -(x-y+9)a+9x=0$$
$$F(a,x,y)=\frac{\partial F(t,x,y)}{\partial a}=0$$
$$\therefore a=\frac{x-y+9}{2}$$
$$(x-y+9)^2 -36x=0$$정리하면
$$(x-y)^2 -18(x+y)+81=0$$이다. 이를 다시 원점을 중심으로 $\pi/4$ 회전하면
$$y=\frac{1}{9\sqrt2}x^2+\frac{9}{2\sqrt2}$$
$$S=2\int_{0}^{\frac{9\sqrt2}{2}} \bigg(\frac{1}{9\sqrt2}x^2+\frac{9}{2\sqrt2}-x\bigg)dx=\frac{27}{2}$$