포물선의 포락선(Envelope)

정리 포물선에서 준선 위의 점 $D$와 초점 $F$의 수직이등분선은 포물선에 접한다.

먼저 포물선 정의에 따라 기하적인 증명을 해보자.

증명보기 1

선분 $DF$의 수직이등분선을 $l$이라 하자.

준선 위의 점 $D$에서 준선에 수직인 직선을 $m$이라 하자.

$l$과 $m$이 만나는 점을 $P$라고 하자.

$$\overline{PD}=\overline{PF}$$

이므로 점 $P$는 포물선 위의 점이다.

이제 직선 $l$이 포물선과 $P$가 아닌 다른 점 $P^{\prime}$에서 만난다고 하자.

$$\overline{P^{\prime}D}=\overline{P^{\prime}F}\;\;(\because p^{\prime}\in l)$$

점 $P^{\prime}$에서 준선에 내린 수선의 발을 $H$라고 하면 $P^{\prime}$이 포물선 위에 있으므로

$$\overline{P^{\prime}H}=\overline{P^{\prime}F}$$

$$\therefore \overline{P^{\prime}D}=\overline{P^{\prime}H}$$

이는 모순이다. 그러므로 수직이등분선 $l$은 접선이다.

방정식으로 증명할 수도 있다.

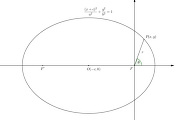
증명보기 2

초점 $F(p,0)$이고 준선 $x=-p$인 포물선 $y^2=4px$를 생각하자.

준선 위의 점을 $D(-p,y_1)$이라 하자.

수직이등분선을 구해보자.

선분 $DF$의 중점은 $M(0, y_1 /2)$이고 기울기는 $-y_1/2p$이므로 수직이등분선의 방정식은

$$y= \frac{2p}{y_1}x+\frac{y_1}{2}$$

포물선 $y^2=4px$와 만나는 점을 구해보자.

$$\bigg(\frac{2p}{y_1}x+\frac{y_1}{2}\bigg)^2=4px$$

정리하면

$$\bigg(\frac{2p}{y_1}\bigg)^2x^2-2px+\bigg(\frac{y_1}{2}\bigg)^2=0$$

$$D/4=p^2 -\bigg(\frac{2p}{y_1}\bigg)^2\bigg(\frac{y_1}{2}\bigg)^2=0$$

그러므로 준선 위의 점 $D$와 초점 $F$의 수직이등분선은 접선이다.

어떤 곡선의 모든 접선의 모임을 포락선으로 부른다. 그러므로 준선 위의 점과 초점의 수직이등분선들은 포물선의 포락선이다. 아래 그림에서 확인할 수 있다.