삼각함수 덧셈정리

덧셈정리를 증명하는 법

코사인 제2 법칙으로 증명

삼각함수 덧셈정리를 증명해보자.

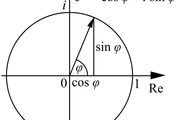
그림에서 두 점은 $P(\cos \alpha , \sin \alpha)$, $Q(\cos \beta , \sin \beta)$이다.

코사인 제 2법칙에 따라

$$\overline{PQ}^2 =\overline{OP}^2 +\overline{OQ}^2 -2 \overline{OP}\cdot \overline{OQ}\cdot \cos( \angle POQ)$$

$$(\cos \alpha -\cos \beta)^2 + (\sin \alpha -\sin \beta)^2 =1+1 -2  \cos( \alpha-\beta)$$

$$\cos^2 \alpha -2\cos \alpha \cos \beta +\cos^2 \beta + \sin^2 \alpha -2\sin \alpha \sin \beta +\sin^2 \beta =1+1 -2 \cdot \cos( \alpha-\beta)$$

$$2-2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )=2 -2  \cos( \alpha-\beta)$$

$$\therefore \cos( \alpha-\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$$

이 식은 항등식이다.

$\beta$ 자리에 $-\beta$를 대입하면

$$\cos( \alpha+\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$ 를 얻는다.

$\alpha$ 자리에 $\displaystyle{\frac{\pi}{2}-\alpha}$를 대입하면

$$\cos\bigg( \frac{\pi}{2}-\alpha-\beta \bigg)=\cos \bigg(\frac{\pi}{2}-\alpha \bigg) \cos \beta +\sin \bigg(\frac{\pi}{2}-\alpha \bigg) \sin \beta$$

$$\sin( \alpha+\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

마찬가지로 $\beta$ 자리에 $-\beta$를 대입하면

$$\sin( \alpha-\beta)=\sin \alpha \cos \beta -\cos \alpha \sin \beta$$

백터 내적으로 기억하기

벡터 내적을 배웠다면 아래와 같이 기억하자.

$$\overrightarrow{OP}\cdot \overrightarrow{OQ}=|\overrightarrow{OP}||\overrightarrow{OQ}|\cos(\alpha-\beta)$$

$$(\cos\alpha,\sin\alpha)\cdot (\cos\beta,\sin\beta)=\cos(\alpha-\beta)$$

$$\therefore \cos( \alpha-\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta$$

다시 정리하면

• 삼각함수 덧셈정리

$$\begin{align} & \quad  \cos( \alpha-\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta \tag{1} \\ & \quad \cos( \alpha+\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta \tag{2}\\ & \quad \sin( \alpha+\beta)=\sin \alpha \cos \beta +\cos \alpha \sin \beta \tag{3}\\ & \quad \sin( \alpha-\beta)=\sin \alpha \cos \beta -\cos \alpha \sin \beta\tag{4} \end{align}$$

덧셈정리를 변형하여 공식 만들기

덧셈정리에서 $\alpha=\beta$로 놓으면 배각 $2\alpha$ 공식을 얻을 수 있고 이를 변형하여 반각 $\displaystyle{\frac{\alpha}{2}}$ 공식을 얻을 수 있다.

• 배각공식

$$\begin{align} & \quad \sin 2\alpha=2\sin \alpha \cos\alpha \tag{1} \\ & \quad \cos 2\alpha=\cos^2 \alpha-\sin^2 \alpha=2\cos^2 \alpha-1=1-2\sin^2\alpha \tag{2} \\ & \quad \tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2 \alpha} \tag{3}\end{align}$$

• 반각공식

$$\begin{align} & \quad \sin^2 \frac{\alpha}{2}=\frac{1-\cos\alpha}{2}\tag{1} \\ & \quad \cos^2 \frac{\alpha}{2}=\frac{1+\cos\alpha}{2} \tag{2}\\ & \quad  \tan^2 \frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha}\tag{3}\end{align}$$

위에 있는 덧셈정리에서 (1)과 (2)를 더하면

$\cos( \alpha+\beta)+\cos( \alpha-\beta)=2\cos \alpha \cos \beta$이다. 이 식을 바꿔서 아래와 같은 공식을 얻을 수 있다.

• 곱을 합차로 고치기

$$\begin{align} &\quad \sin \alpha \cos \beta =\frac{1}{2}\{\sin( \alpha+\beta)+\sin( \alpha-\beta)\} \tag{1} \\ & \quad \cos \alpha \sin \beta =\frac{1}{2}\{\sin( \alpha+\beta)-\sin( \alpha-\beta)\} \tag{2} \\ & \quad \cos \alpha \cos \beta =\frac{1}{2}\{\cos( \alpha+\beta)+\cos( \alpha-\beta)\} \tag{3} \\ & \quad \sin \alpha \sin \beta =-\frac{1}{2}\{\cos( \alpha+\beta)-\cos( \alpha-\beta)\} \tag{4} \end{align}$$

• 합차를 곱으로 고치기

$$\begin{align}&\quad \sin A +\sin B=2 \sin \frac{A+B}{2}\cos\frac{A-B}{2} \tag{1} \\ & \quad \sin A -\sin B=2 \cos \frac{A+B}{2}\sin\frac{A-B}{2} \tag{2}\\ & \quad \cos A +\cos B=2 \cos \frac{A+B}{2}\cos\frac{A-B}{2} \tag{3} \\ & \quad \cos A -\cos B=-2 \sin \frac{A+B}{2}\sin\frac{A-B}{2} \tag{4} \end{align}$$

삼각함수의 합성

덧셈정리를 써서 두 파동이 중첩되었을 때 만들어지는 새로운 파동을 나타내는 식을 구할 수 있다. 이것을 수학 시간에는 삼각함수의 합성이라 부른다. 

$a\sin\theta+b\cos\theta(a\not=0,\;\;b\not=0)$을 $r\sin(\theta+\alpha)$와 같은 꼴로 고쳐보자. (단, $r>0,\;\;0\leq \alpha<2\pi$)

사인으로 만들기

그림과 같이 좌표평면 위에 점 $P(a,b)$를 잡고, 동경 $OP$가 $x$축 양의 방향과 이루는 각의 크기를 $\alpha$라고 하면 $\overline{OP}=\sqrt{a^2 +b^2}$이다.

따라서

$$\sin\alpha=\frac{b}{\sqrt{a^2 +b^2}},\;\;\cos\alpha=\frac{a}{\sqrt{a^2 +b^2}}$$ 이다.

$$\begin{align} \therefore \;\; a\sin \theta+b \cos \theta \;\;&=\;\; \sqrt{a^2 +b^2} \left(\frac{a}{\sqrt{a^2 +b^2}} \sin \theta+ \frac{b} {\sqrt{a^2 +b^2}}\cos\theta\right) \\&=\;\;\sqrt{a^2 +b^2}(\cos\alpha\sin\theta+\sin\alpha\cos\theta)\\&=\;\;\sqrt{a^2 +b^2}\sin(\theta+\alpha) \end{align}$$

 

코사인으로 만들기

한편 $\alpha$의 여각을 $\beta$라고 하면 코사인으로 바꿀 수 있다.

$\displaystyle{\beta=\frac{\pi}{2}-\alpha}$라고 하면

$$\sin\beta=\frac{a}{\sqrt{a^2 +b^2}},\;\;\cos\beta=\frac{b}{\sqrt{a^2 +b^2}}$$ 이다.

$$\begin{align} \therefore \;\; a\sin \theta+b \cos \theta \;\;&=\;\; \sqrt{a^2 +b^2} \left(\frac{a}{\sqrt{a^2 +b^2}} \sin \theta+ \frac{b} {\sqrt{a^2 +b^2}}\cos\theta\right) \\&=\;\;\sqrt{a^2 +b^2}(\sin\beta\sin\theta+\cos\beta\cos\theta)\\&=\;\;\sqrt{a^2 +b^2}\cos(\theta-\beta) \end{align}$$