2020학년도 서울대 면접 수학 기출문제_02

문제 2 실수 $a<b$에 대하여 닫힌구간 $[a,b]$가 주어졌을 때, 함수 $y=f_{[a,b]}(x)$를 실수 전체의 집합에서 다음과 같이 정의하자.

$$f_{[a,b]}(x)=\begin{cases}a+b-x\quad\quad&(x\in[a,b])\\x\quad\quad&(x\not\in[a,b])\end{cases}$$

2-1. 합성함수 $y=(f_{[0,2]}\circ f_{[1,3]})(x)$는 $x=1$,$2$에서 연속인지 아닌지 설명하시오.

2-2. 모든 실수 $x$에 대하여 $(f_{[0,1]}\circ f_{[a,b]})(x)=(f_{[a,b]}\circ f_{[0,1]})(x)$ 가 성립하도록 하는 점 $P(a,b)$를 모두 구하시오. (단, 실수 $a,b$의 범위는 $0\leq  a< b \leq 1$이다.)

풀이

1-1

먼저, 함수 $f_{[a,b]}$의 그래프를 그려보자.

$x\in[a,b]$일 때 $(a,b)$와 $(b,a)$를 지나고 기울기가 $-1$인 직선이고 $x\not \in [a,b]$일 때는 항등함수인 $y=x$이다.

 

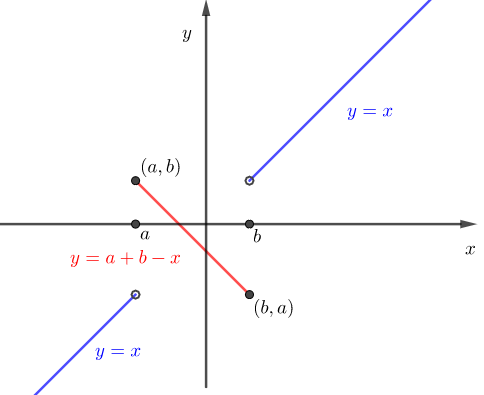
따라서 $y=f_{[1,3]}(x)$와 $y=f_{[0,1]}(x)$의 그래프는 각각 아래와 같다.

 

$$y=f_{[1,3]}(x)\quad\quad\quad\quad\quad\quad\quad\quad\quad y=f_{[0,1]}(x)$$

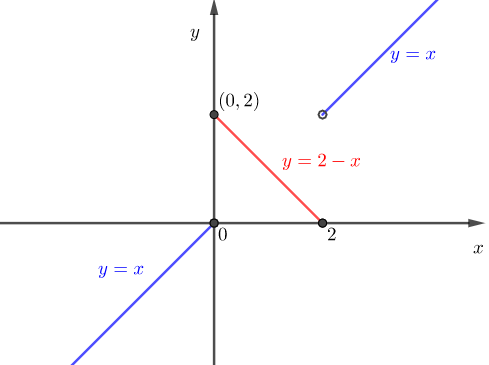
두 함수를 합성하기 위해서 함숫값 $f_{[1,3]}(x)$을 조사해서 구간 $[0,2]$에 포함되는가를 따져야 한다.

$0<x<1$일 때, $0<f_{[1,3]}(x)<1$이므로 $(f_{[0,2]}\circ f_{[1,3]})(x)=2-x$

$1\leq x<2$일 때, $2<f_{[1,3]}(x)\leq 3$이므로$(f_{[0,2]}\circ f_{[1,3]})(x)=4-x$

$2\leq x \leq 3$일 때, $1 \leq f_{[1,3]}(x)\leq 2$이므로 $(f_{[0,2]}\circ f_{[1,3]})(x)=2-(4-x)=x-2$

$x<0$, $3<x$일 때는 $(f_{[0,2]}\circ f_{[1,3]})(x)=x$

아래와 같이 그래프를 그려서 $x=1,2$에서 불연속임을 확인할 수 있다.

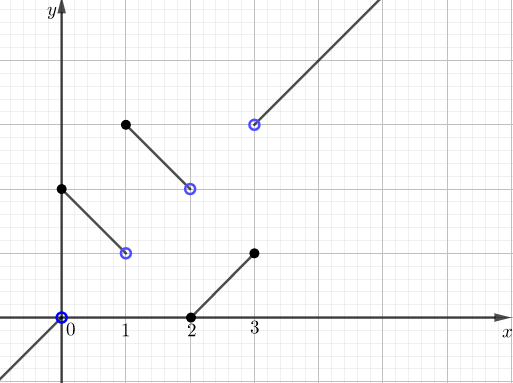
2-2

함수 $y=f_{[0,1]}(x)$의 그래프는 아래와 같다.

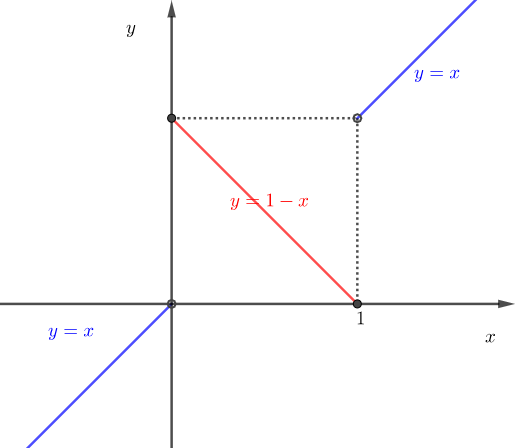
함수 $y=f_{[a,b]}(x)$의 그래프는 실수 $a,b$의 범위가 $0\leq  a< b \leq 1$로 주어졌으므로 아래와 같다.

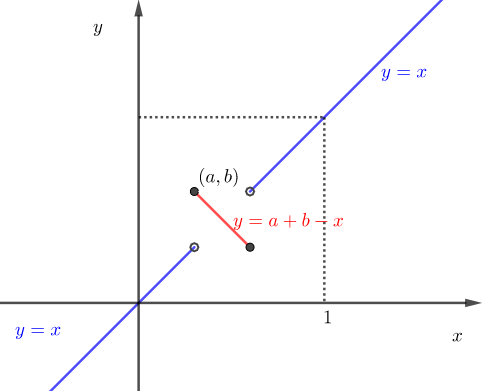
이 두 함수를 합성한 함수를 생각하자.

$(f_{[0,1]}\circ f_{[a,b]})(x)=(f_{[a,b]}\circ f_{[0,1]})(x)$를 만족시키려면 $a,b$는 어떻게 결정해야 하는가를 찾으면 된다.

$$1-(a+b-x)=a+b-(1-x)$$

$$\therefore\;\;\;a+b=1$$

따라서 점 $P(,a,b)$를 집합으로 나타내면 아래와 같다.

$$\{(a,b)\;\;|\;\;a+b=1,\;\;0\leq a < b \leq 1\;\;\}$$

여기까지는 공통 문제이고 자연 과정 문제는 조금 더 복잡하다.

문제 2 실수 $a<b$에 대하여 닫힌구간 $[a,b]$가 주어졌을 때, 함수 $y=f_{[a,b]}(x)$를 실수 전체의 집합에서 다음과 같이 정의하자.

$$f_{[a,b]}(x)=\begin{cases}a+b-x\quad\quad&(x\in[a,b])\\x\quad\quad&(x\not\in[a,b])\end{cases}$$

2-1. 합성함수 $y=(f_{[0,2]}\circ f_{[1,3]})(x)$의 $x=1$,$2$, $3$에서의 값을 구하시오. 또, 부등식

$$(f_{[0,2]}\circ f_{[1,3]})(x) \geq x+1 $$

을 만족하는 $x$값의 범위를 구하시오.

2-2. 두 함수

$$y=x^2,\quad y=(f_{[0,1]}\circ f_{[a,a+1]})(x)$$의 그래프라 좌표평면 위의 서로 다른 두 점에서 만나도록 하는 상수 $a$의 값의 범위를 구하시오. (단, $a$의 범위는 $0\leq a \leq 1$이다.)

2-3. 모든 실수 $x$에 대하여 $(f_{[0,1]}\circ f_{[a,b]})(x)=(f_{[a,b]}\circ f_{[0,1]})(x)$가 성립하도록 하는 점 $P(a,b)$의 영역을 구하시오. (단, $a$는 음이 아닌 실수이다.)

풀이

1번은 공통 문제에 있는 그래프를 참고하면 아주 쉽게 해결할 수 있으므로 생략.

2번부터 보자.

두 함수를 합성해 보면 위에서와 마찬가지로 네 구간으로 나누어서 방정식을 따로 구하면 된다.

1. $x<0$일 때, $f_{[0,1]}(f_{[a,a+1]}(x))=x$
2. $0\leq x <a$일 때, $f_{[0,1]}(f_{[a,a+1]}(x))=1-x$
3. $a \leq x < 2a$일 때, $f_{[0,1]}(f_{[a,a+1]}(x))=2a+1-x$
4. $2a \leq x \leq a+1$일 때, $f_{[0,1]}(f_{[a,a+1]}(x))=1-(2a+1-x)=x-2a$
5. $a+1 <x$일 때, $f_{[0,1]}(f_{[a,a+1]}(x))=x$

예를 들어 $a=0$이면 합성한 함수가 $y=x$이므로 포물선 $y=x^2$과 두 점에서 만난다. $a$가 적당히? 작다면 아래와 같이 두 점에서 만남을 알 수 있다. 이런 상황은 $y=x-2a$가 포물선과 접할 때까지 지속될 것이다.

판별식으로 $a$값을 구하면

$$x-2a=x^2\quad x^2 -x+2a=0\quad \therefore \;\;a=\frac{1}{8}\tag{1}$$

여기서 끝나지 않는다. $a$가 적당히 커지면 아래 그림과 같이 두 점에서 만날 수 있다. 이 상황은 직선 $y=1-x$와 포물선 $y=x^2$이 만날 때이다.

$$x^2 =1-x\quad x^2 +x-1=0\quad \therefore\quad x=\frac{-1\pm\sqrt{5}}{2}$$

따라서 $\displaystyle{a>\frac{-1+\sqrt{5}}{2}}\tag{2}$이면 두 점에서 만난다.

(1),(2)에 따라서 포물선과 두 점에서 만나게 하는 $a$값의 범위는 아래와 같다.

$$0\leq a <\frac{1}{8} ,\quad\quad \frac{-1+\sqrt{5}}{2}<a \leq 1$$

마지막으로 3번은 공통 문제 풀이를 참고하여 아래와 같음을 확인하면 된다.

$$\{(a,b)\;\;|\;\;a+b=1,\;\;0\leq a < b \leq 1\;\;\}\cup \{(a,b)\;\;|\;\;1<a<b\;\;\}$$

서울대는 면접관이 풀이 과정을 살펴볼 수 있을 만큼 아주 가까운 거리에 있으므로 답에 이르는 과정을 세세하게 평가할 것이라 생각한다. 어쩌면 중간 과정은 과감하게 생략하고 수학적 추측으로(예: 접할 때를 기준이 된다.) 답에 빠르게 접근하는 것도 좋은 방법이 될 것이다. 면접 연습을 할 때 누군가를 가르치듯이 모든 것을 설명하려고 하는 학생들을 많이 본다. 면접관은 대부분 수학 전공자이다. 상당한 고수이므로 구구절절한 설명을 필요 없다. 면접은 누굴 가르치는 것이 아니라 고수에게 실력을 보여주는 '오디션'임을 명심하라. 아무튼 이 글을 본 모든 학생들이 최선을 다해서 좋은 결과를 얻기를 바란다.

 

admission.snu.ac.kr/undergraduate/notice?md=v&bbsidx=127422

2020학년도 서울대학교 입학전형 선행학습 영향평가 - 공지사항 - 대학 - 입학 - 서울대학교 입학�