신경망 첫걸음

'수포자도 이해하는 신경망 동작 원리와 딥러닝 기초'라는 표지 글에 끌려서 읽었다. 아주 쉽게 쓰여졌지만 수포자가 이해하기는 어려울 듯하다. 새로 알게 된 활성화 함수에 대해 정리해 둔다.

생물학적 뇌의 기본 단위는 뉴런(신경세포: neuron)이다. 종류에 상관없이 모든 뉴런은 한쪽 끝에서 다른 쪽 끝으로 전기신호를 보낸다. 가지돌기(dendrite)에서 축삭(axon)을 거쳐 축삭말단(axon terminal)까지 보낸다. 이런 식으로 신호를 하나의 뉴런에서 다른 뉴런으로 계속해서 전달하는데 우리 몸은 이런 과정을 통해 빛, 소리 등 다양한 감각을 인지할 수 있게 된다. 감각 뉴런으로부터 전달된 신호는 신경계를 통해 뇌로 전달되는데 뇌도 뉴런으로 만들어져 있다.

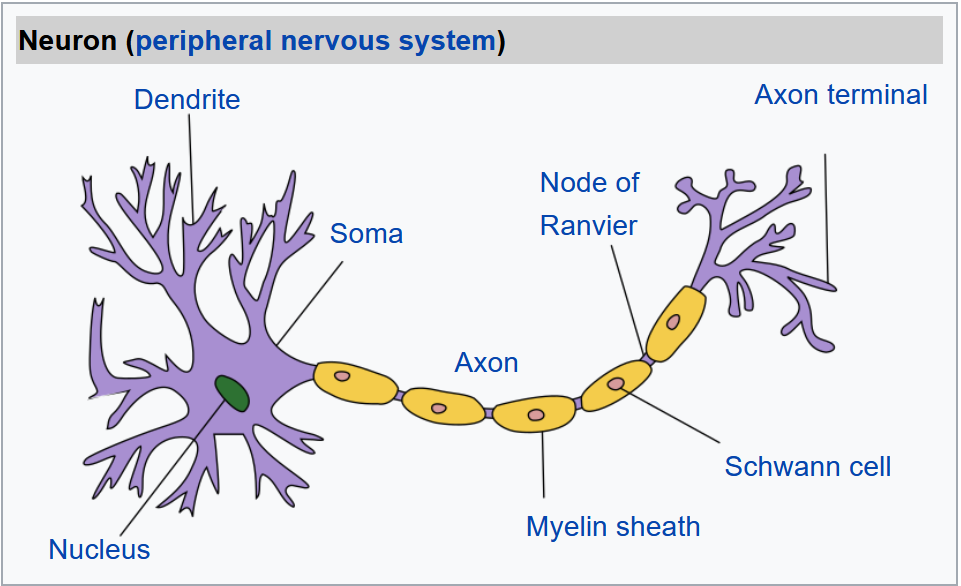
생물에서 배웠을 터인데 기억은 나지 않는다. 잘 몰라도 대충 이해는 간다. 아무튼 뉴런은 모든 신호를 전달하지만 약한 것은 중간에 사라진다. 입력된 신호가 어떤 분계점(threshold)에 도달해야 출력이 발생한다. 이 과정을 알고리즘으로 만들 때 입력 신호를 받아 특정 분계점을 넘어설 때 출력 신호를 만드는 함수가 필요하다. 바로 이 일을 하는 함수가 활성화 함수이다.

활성화 함수

입력 신호가 특정 분계점을 넘었을 때만 출력 신호를 생성하는 함수

활성화 함수 가운데 가장 간단한 함수는 계단 함수(step function)이다. 계단 함수를 어디다 쓰나 했더니 이런 곳에 쓰고 있었다.

$$f(x)=\cases{1 \quad\quad x \geq \frac{1}{3}\\0\quad\quad x<\frac{1}{3}}$$

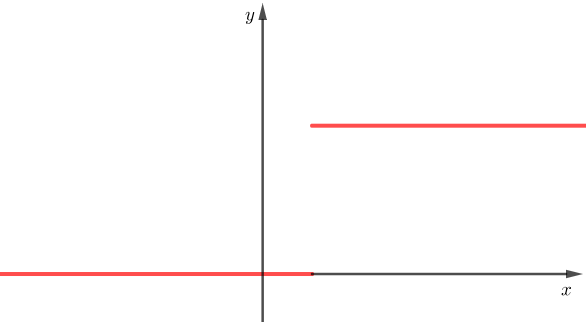
위 함수는 $0<x,1/3$을 분계점으로 생각할 수 있다. 계단 함수는 딱딱하고 차갑고 자연스럽지 않으므로 부드럽게 개선할 필요가 있다. 기왕이면 미적분이 가능한 연속 함수로 만들어야 한다. 아래 녹색 그래프를 가지는 함수가 좋겠다. 이렇게 $S$ 모양 그래프를 가지는 함수를 시그모이드(sigmoid) 함수라고 한다.

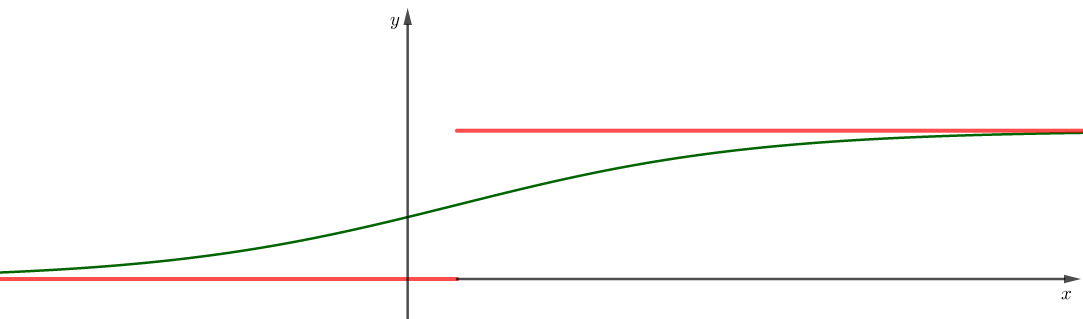
$$f(x)=\frac{1}{1+e^{-x +\frac{1}{3}}}$$

함수식은 훨씬 복잡해 보이지만 이것이 오히려 자연스러운 곡선이다. 오죽하면 $e$를 밑으로 하는 로그를 자연 로그로 부르겠는가!

미분 방정식 가운데 시그모이드 함수인 로지스틱 함수(logistic function)를 해로 가지는 방정식은 아래와 같다.

$$y^{\prime}=y(1-y),\;\;y(0)=\frac{1}{2}$$

풀이는 아래와 같다.

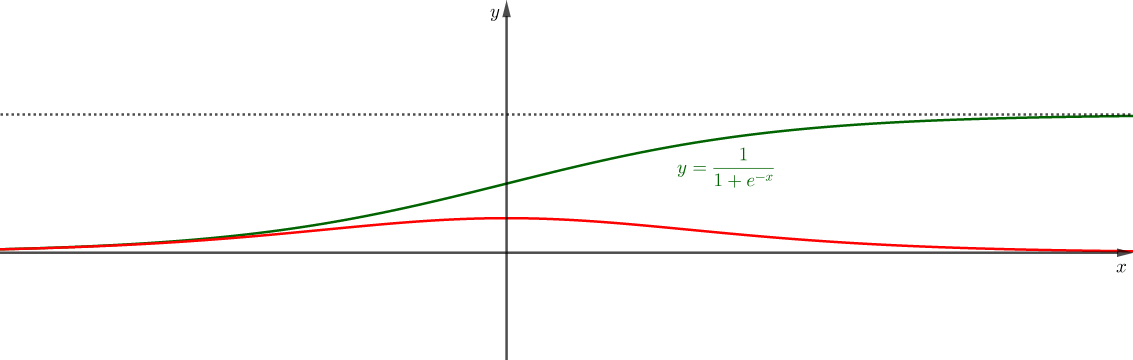
$$\begin{split}\frac{1}{y(1-y)}\frac{dy}{dx}&=1 \\ \bigg(\frac{1}{y}+\frac{1}{1-y}\bigg)dy&=dx\\ \ln \frac{y}{1-y}&=x +C\\ \frac{y}{1-y}&=Ae^{x} \\ y&=\frac{Ae^x}{1+Ae^{x}}\quad\quad \because \;\; y(0)=\frac{1}{2}\Rightarrow A=1\\ y&=\frac{1}{1+e^{-x}}\end{split}$$

위 함수와 도함수의 그래프는 아래와 같다.

활성화 함수로 쓸 수 있는 다른 함수도 소개한다.

$$y=\frac{\tanh x}{2}+\frac{1}{2}$$

쌍곡 함수인 하이퍼볼릭 탄젠트 함수는 아래와 같다. 어쨌든 오일러 상수인 $e$가 들어 간다.

$$\tanh x = \frac{\sinh x}{\cosh x}=\frac{e^x -e^{-x}}{e^x +e^{-x}}$$

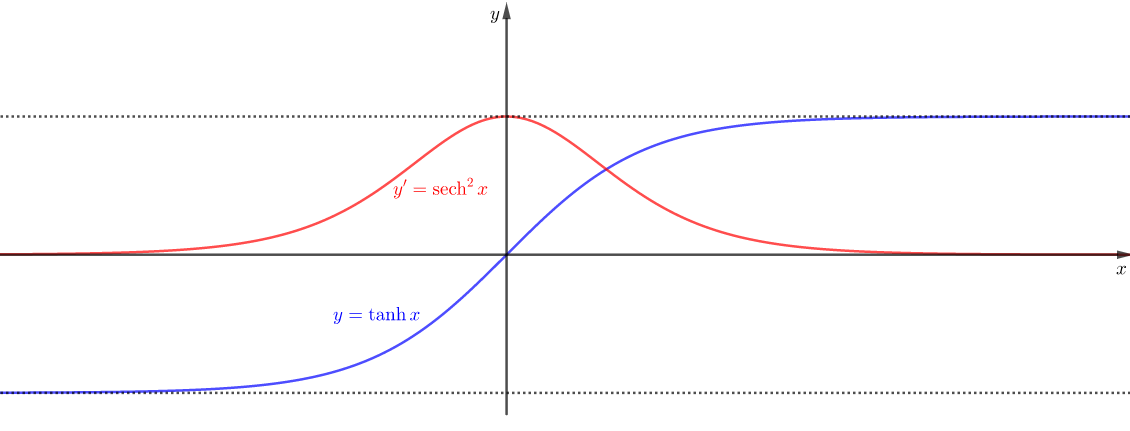
하이퍼볼릭 탄젠트 함수와 도함수의 그래프는 아래와 같다.

소개한 함수가 가진 단점을 보완하는 함수로 아래와 같은 함수를 쓰고 있다고 한다.

• 수정한 선형 단위 함수: ReLU 함수 (Rectified Linear Unit)     $$\Rightarrow f(x)=max(0,x)$$
• 약한 아르이엘유 함수: Leakly ReLU          $$\Rightarrow f(x)=max(0.01 x,x)$$
• 매개변수(parameter)가 있는 아르이엘유 함수: PReLU        $$ \Rightarrow f(x)=max(\alpha x, x)$$
• 지수적 선형 단위 함수: Exponential Linear Unit(ELU)   $$\Rightarrow f(x)=\cases{x\quad\quad\quad  x>0\\ \alpha(e^x -1)\quad  x\leq 0}$$

max함수는 둘 가운데 큰 것을 고르는 함수이다. 수학 시간에 한 번은 보았을 함수다. 결론은 수학은 역시 쓸모가 많다는 것이다.