조립제법(Synthetic Division)

졸업을 앞둔 중학교 3학년 아이들에게 진학한 다음에 조금이나마 도움이 될까 싶어서 수업시간에 고교과정을 몇 시간 다루려고 한다. 법으로 선행학습을 금지하고 있지만 어차피 학원에서 다 하고 있으니 학교에서도 한두 시간 가르친다고 죄가 되지는 않을 것이다.

고등학생은 조립제법으로 나눈다

조립제법은 다항식의 나눗셈에서 계수만 따로 떼어내 간편하게 셈하는 방법이다. 아주 간단한 방법이긴 하지만 그래도 처음 배우는 학생은 실수할 수도 있다. 어차피 고등학생이 되면 자세하게 배우므로 부담 없이 살펴보면 된다.

 

다시 정리해 보자. 

아래는 $(x^3 +2x^2 -3x +1)\div(x+1)$을 조립제법으로 몫과 나머지를 구하는 과정이다.

별달리 어려운 개념은 없어서 따로 강조하여 설명할 부분이 없다. 하지만 어설프게 외워서 쓰다 보면 실수를 하게 되므로 조심해야 한다. 특히, 내림차순으로 정리했을 때, 중간에 차수가 비는 자리는 반드시 계수인 $0$을 써야함을 명심하자.

연습문제

1. $(x^3 -2x^2 +3x +1)\div(x+1)$

2. $(x^3 +3x^2 -x -1)\div(x-2)$

3. $(x^3 -3x +1)\div(x-1)$

조립제법이 쓸모는 있지만 일차항 계수가 1일 때만 쉽게 쓸 수 있다. (참고: 최고차항 계수가 1인 다항식은 monic polynomial이다.) 

일차항의 계수가 1이 아닐 때는 어떻게 할 것인가?

이제 나누는 다항식이 일차항의 계수가 1이 아닐 때 조립제법을 쓰는 방법을 알아보자.

위에서 보인 계산을 조립제법으로 구한 몫과 나머지를 써서 식을 다시 정리해 보자.

$$x^3 +2x^2 -3x+1=(x+1)(x^2 +x-4)+5$$

다항식 $A(x)$를 $B(x)$로 나누었을 때, 몫이 $Q(x)$이고 나머지가 $R(x)$라면 아래와 같이 정리할 수 있다. 여기서 나머지 $R(x)$의 차수는 $B(x)$의 차수보다 작다.

$$A(x)=B(x)Q(x)+R(x)$$

이제 다항식 $x^3 +2x^2 -3x+1$를 $2x-1$로 나누었을 때 몫이 $Q(x)$, 나머지는 $R$로 생각하자. 일차식으로 나누므로 나머지는 상수항이 된다.

$$x^3 +2x^2 -3x+1=(2x-1)Q(x)+R$$

이 식을 다시 고쳐보자.

$$x^3 +2x^2 -3x+1=2\bigg(x-\frac{1}{2}\bigg)Q(x)+R$$

다항식 $\displaystyle{x-\frac{1}{2}}$로 나눈 몫은 $2Q(x)$이고 나머지는 $R$이다.

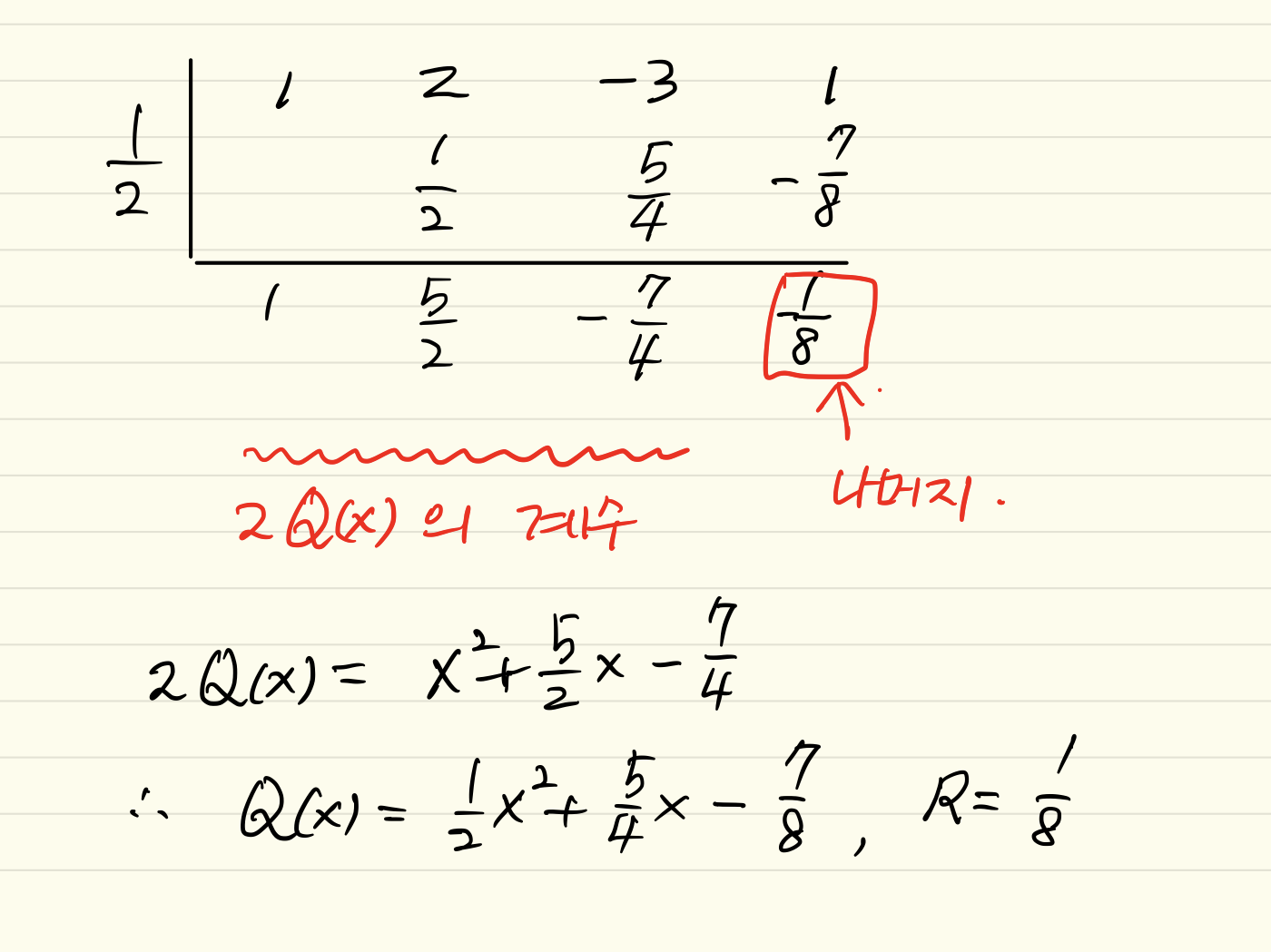
이체 1차식으로 나눌 때 언제나 조립제법을 써서 계산할 수 있게 되었다. 

연습문제

1. $(x^3 -2x^2 +x -1)\div(2x+1)$

2. $(x^3 +x^2 -x -1)\div(3x-2)$

3. $(x^3 -3x^2 +1)\div(2x-1)$

위에 정리된 과정을 톺아보면 자연스럽게 아래와 같은 나머지 정리를 알 수 있다.

다항식 $P(x)$를 다항식 $x-\alpha$로 나눈 나머지는 $R=P(\alpha)$이다.

다항식 $P(x)$를 다항식 $\alpha x-\beta$로 나눈 나머지는 $\displaystyle{R=P\bigg(\frac{\beta}{\alpha}\bigg)}$이다.

 

아래 연결한 위키 문서를 보면 이차식으로 나누는 조립제법도 나오지만 직접 나누는 것과 큰 차이가 없어서 따로 기억할 필요는 없다.

https://en.wikipedia.org/wiki/Synthetic_division

Synthetic division - Wikipedia