여러 가지 평균의 대소 관계

수학에서 쓰는 평균(Mean)은 여러 가지가 있다. 이들을 구별해 보자.

1. 산술평균: Arithmatic Mean

가장 많이 쓰는 평균이다. 등차수열에서 등차중항을 구하는 방법을 생각하면 된다. $a,\;AM,\;b$은 등차수열이면 $b-AM=AM-a$이다.

$$AM=\frac{a+b}{2}$$

2. 조화평균: Hamonic Mean  

$\displaystyle{\frac{1}{a},\;\frac{1}{HM},\;\frac{1}{b}}$이 등차수열을 이루면 $a,\;HM,\;b$은 조화수열이 된다.

$$HM=\frac{2ab}{a+b}=\frac{2}{\dfrac{1}{a}+\dfrac{1}{b}}$$

3. 기하평균: Geometric Mean

$a,\;GM,\;b$은 등비수열이면 $b/GM=GM/a$이다. 가로와 세로의 길이가 $a,\;b$인 직사각형과 넓이가 같은 정사각형은 한 변의 길이가 $\sqrt{ab}$이다. 

$$GM=\sqrt{ab}$$

4. 제곱 평균의 제곱근: Root Mean Square 또는 이차평균: Quadratic Mean

통계에서 분산을 구할 때 편차 제곱의 평균을 구하고 분산의 양의 제곱근을 표준편차라고 한다. 이 표준편차와 같은 것으로 생각하면 된다.

$$RMS=\sqrt{\frac{a^2 +b^2}{2}}$$

두 수 $a,\;b$의 평균들 사이에 아래와 같은 부등식이 성립한다.($a=b$일 때 등호 성립)

$$HM\leq GM\leq AM \leq RMS$$

$$\frac{2ab}{a+b}\leq\sqrt{ab}\leq \frac{a+b}{2}\leq\sqrt{\frac{a^2+b^2}{2}}$$

이 부등식이 성립함을 보여주는 그림은 아래와 같다. 별다른 설명 없이 아래 그림을 모두 이해한다면 기하적 감각이 매우 뛰어나다고 할 수 있다.

 

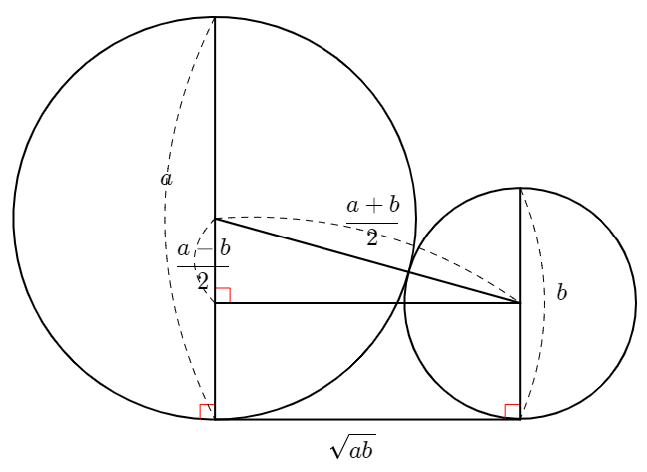
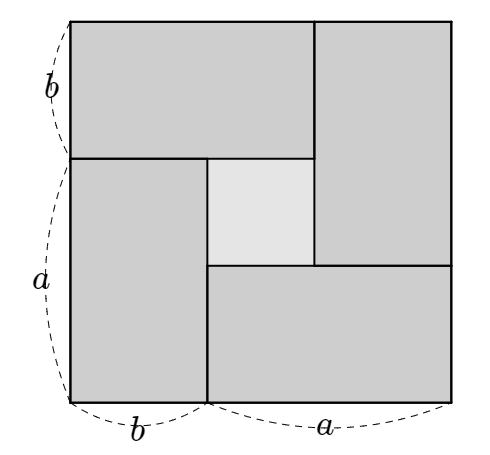
$$(a+b)^2-(a-b)^2=4ab$$

$$\frac{a+b}{2} \geq \sqrt{ab}$$

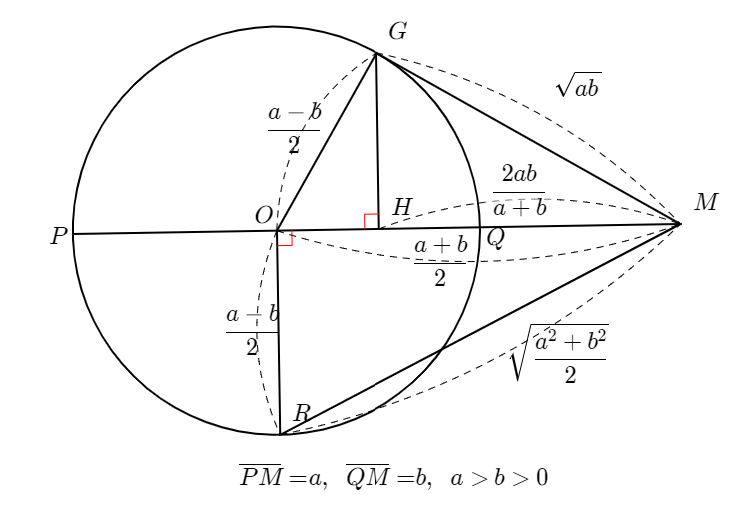
$$HM<GM<AM<RMS$$