루빅스 큐브 고급 공식

차례

한때 열심히 연습해서 5분대까지 기록했는데 한동안 손을 놓았더니 이젠 공식도 가물가물하다. 또다시 정리하면서 연구를 해보려고 한다. 초급 공식보다는 조금 더 빠르게 맞출 수 있는 공식인 프리드리히 공식을 정리한다. 영어로 된 사이트를 그대로 우리말로 옮기는 정도에 불과하다. 영어를 잘하는 사람은 당연히 링크된 곳을 찾으면 되지만 영어가 서툰 사람은 이 글을 보면 좋겠다.

프리드리히 공식 CFOP

먼저 공식을 표기하는 법은 아래와 같다. 시계방향으로 돌리는 것은 각각 Front, Right, Left, Up, Down, Back의 맨 앞글자를 떼서 표현하고 반시계방향은 ${}^{\prime}$을 붙인다. 영어를 잘하는 사람은 링크를 따라가면 된다. 루빅스 큐브 공식 표기법

 

하얀 십자가 White Cross

대부분 흰 면을 맨 아래에 두고 먼저 맞춘다. 흰 십자가와 옆면 파랑, 빨강, 녹색, 주황의 가운데까지 맞추는 것이다. 이것은 굳이 공식이 없어도 맞출 수 있지만 빠르게 맞추려면 외우면 좋다. 눈으로 보면서 맞추면 좀처럼 시간이 줄지 않는다. 흰 면을 바닥에 두고 보지 않고 맞추는 연습을 해야 한다.

1,2층 맞추기 First two layers - F2L

다음 단계는 아래에 있는 두 층을 맞춘다. 초보 공식은 한 층씩 맞추지만 프리드리히 공식은 두 층을 한꺼번에 맞출 수 있어서 시간을 크게 줄일 수 있다. 흰색이 있는 꼭짓점 조각을 3층으로 올리고 모서리 조각과 짝을 짓고 한꺼번에 아래로 내린다. 41가지 경우가 있는데 대부분 직관적으로도 해결할 수 있다. 1단계에서 이미 맞추어 둔 십자가에 있는 면 조각의 색을 보면서 짝을 지을 조각의 색을 정하면 된다.

1단계에서 맞춘 십자가를 흐트러트리지 않도록 주의하면서 맞춰야 한다. 모양은 비슷하지만 때때로 2번 돌려야 해서 공식을 모두 구분해서 외우기는 매우 어렵다.

FU2F${}^{\prime}$으로 해도 되지만 이미 맞춘 주황색 조각이 흐트러진다. 이럴 때 U${}^{\prime}$RU2R${}^{\prime}$를 써야 한다.

아주 쉬울 때

꼭짓점 조각은 1층에 모서리 조각은 3층에 있을 때

꼭짓점 조각은 3층에 모서리 조각은 2층에 있을 때

d는 아래 2개 층을 한꺼번에 돌리는 걸 나타낸다. 소문자로 쓴 다른 것도 마찬가지로 2개 층을 같이 돌리는 것을 뜻하고 방향은 문자를 따른다.

꼭짓점 조각과 모서리 조각이 모두 3층에 있고 흰 면이 바깥을 향할 때

꼭짓점 조각과 모서리 조각이 모두 3층에 있고 흰 면이 위를 향할 때

꼭짓점 조각은 1층에 변 조각은 2층에 있을 때

 

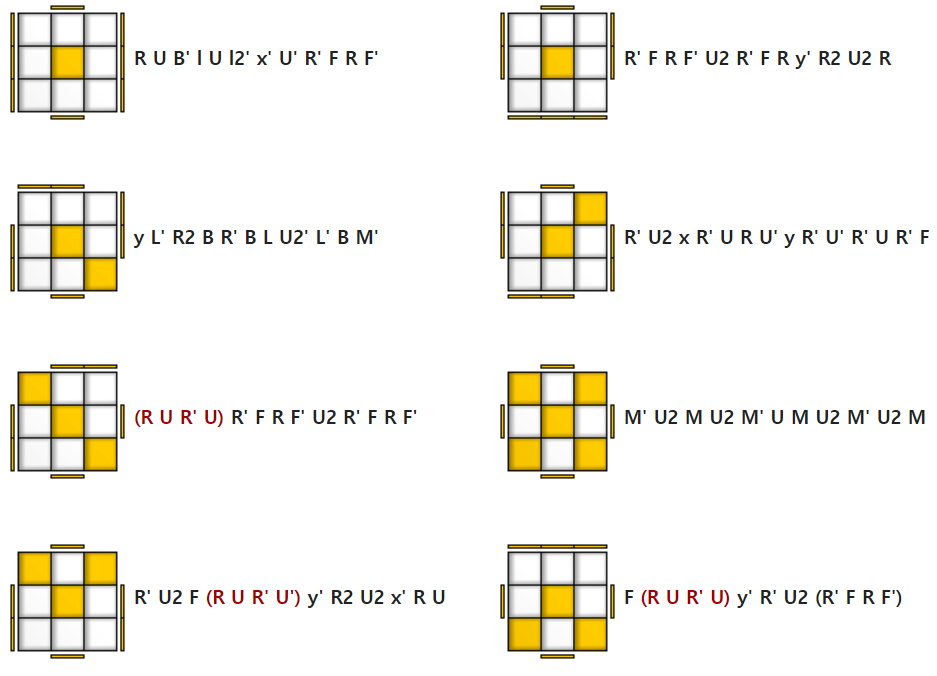
3층 방향 정하기 Orient last layer - OLL 

3층의 윗면을 모두 노란색이 되도록 만드는 단계다. 큐브 전체를 돌리는 기호 x, y, z는 아래와 같은 방향으로 돌린다.

x: Right와 같은 방향 y: Up과 같은 방향 z: Front와 같은 방향

점

선

십자가

네 꼭짓점

모양 ㅣ

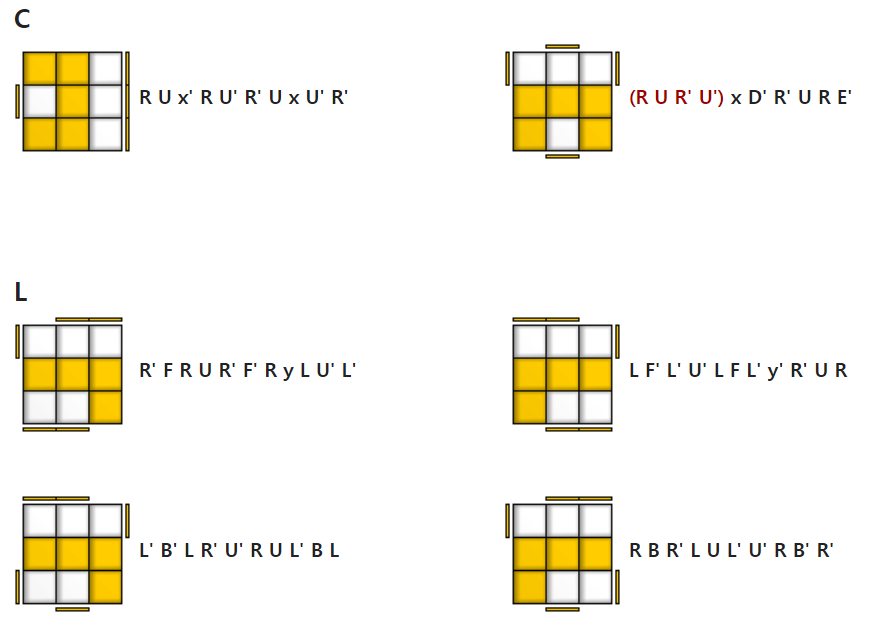
C, L

P, T

W, Z

http://www.rubiksplace.com/speedcubing/OLL-algorithms/

OLL Algorithms - CFOP SpeedSolving OLL #57 Cases

 

3층 돌려 맞추기 Permutate the last layer - PLL

이제 마무리 단계다. 공식없이 맞추는 일은 불가능하다. 많이 알면 좋지만 많이 쓰는 몇 가지만 알아도 된다.

조만간 큐브와 관련된 수학을 정리할 계획이다. 주로 대수학의 대칭군과 관계된 내용이 될 것이다. 아래에 아주 잘 정리된 또 다른 사이트도 있다

https://jperm.net/

J Perm | Speedcubing Tutorials