일차함수에서 이차함수로

함수를 중학교 수준에서 다루자면 아래와 같이 말할 수 있다.

변수 $x$의 값에 따라서 변수 $y$의 값이 하나씩 잘 정해지면 $y$는 $x$의 함수라고 한다

더 거칠게 말하면 변수 $y$를 구하는 식에 변수 $x$가 포함되어 있으면 '$y$는 $x$의 함수'이다. 함숫값을 구하는 식에 따라 함수를 분류한다. 중학교에서 일차함수와 이차함수만 다룬다.

다가서기

둘레의 길이가 $10$인 직사각형이 있다. 가로의 길이에 따라서 세로의 길이가 정해진다. 가로와 세로의 길이가 정해지면 넓이도 정해진다. 세로의 길이나 넓이를 구하는 식에는 가로의 길이가 포함되어 있다. 따라서 세로의 길이나 넓이는 가로의 길이의 함수이다.

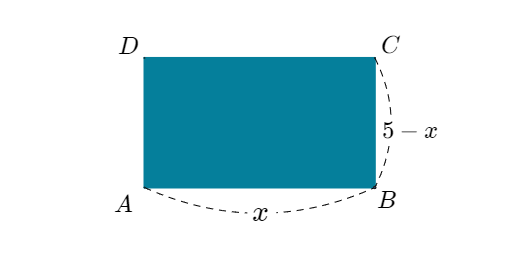
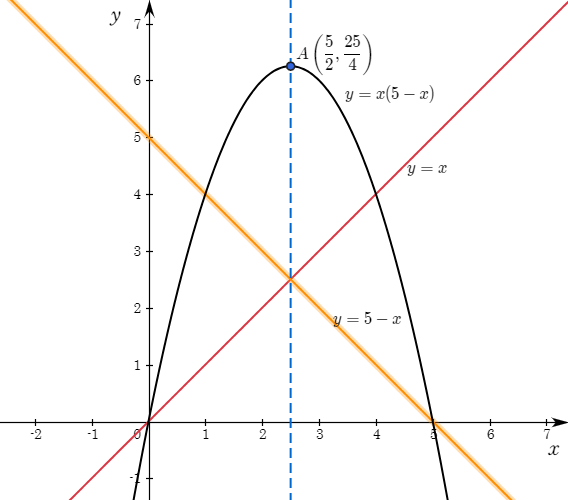
먼저 가로의 길이를 $x$, 세로의 길이를 $y$라고 하자. 둘레의 길이가 10이므로 두 변수 사이의 관계식인 함수식은 아래와 같다.

$$y=5-x$$

일차함수이다.

다음으로 가로의 길이를 $x$, 넓이를 $y$라고 하면 함수식은 아래와 같다.

$$y=x(5-x)$$

함수 $y=x$도 일차함수다. 따라서 이차함수인 넓이는 일차함수인 가로와 세로의 길이의 곱으로 생각하면 쉽게 이해할 수 있다. 일차함수의 그래프는 모두 직선이므로 당연히 이차함수의 그래프도 특별한 모양이 될 것이다. 결론부터 적으면 이차함수의 그래프는 포물선이다.

이차함수 $y=x^2$와 $y=-x^2$의 그래프

일차함수는 항등함수인 $y=x$에서 출발하면 쉽게 이해할 수 있다. 함수는 변수 둘의 변화를 한꺼번에 살피기 위해 주로 그래프를 그려서 관찰한다.

함수 $y=f(x)$의 그래프는 순서쌍 $(x, f(x))$를 모은 집합이라고 말할 수 있다. 집합은 쉽지 않아서 교육과정에서 제외되었다. 이제 집합으로 정의하는 엄밀함은 대학 교재에서나 만날 수 있다. 위에 있는 그림에서 두 함수 $y=x$와 $y=5-x$의 곱을 직관적으로 구하기는 쉽지 않다. 모든 어렵고 복잡한 것은 쉽고 간단한 것으로 분해할 수 있다. 따라서 어려움을 이겨내려면 가장 쉬운 것으로 되돌아가서 출발하면 된다.

가장 간단한 일차함수는 $y=x$이다. 사실 모든 함수는 바로 이 간단한 일차함수에서 출발한다.

아래 그림에서 붉은 색 직선 위에 있는 점 $A(a,a)$가 녹색 곡선 위의 점 $B(a,a^2)$으로 옮겨진다고 생각하면 된다. 

1) $0<a<1$일 때는 $a^2<a$이므로 아래쪽으로 옮겨진다.

2) $a>1$일 때는 $a<a^2$이므로 위쪽으로 옮겨진다.

3) $a=0, a=1$일 때는 $a=a^2$이므로 제자리에 있다. 

4) $a<0$일 때는 $(-a)^2=a^2$이므로 점 $B$와 점 $C$는 $y$축에 대칭임을 생각하자.

 

https://www.algeomath.kr/algeo/algeomath/app/key/a368c8ae32be11efb343f220ef6cc976/view.do

이차함수의 그래프03 | Algeomath

 

이것을 정리하면 $y=x^2$의 그래프는 아래와 같은 성질을 가진다.

1. 원점을 지나며 아래로 볼록한 곡선이다.
2. $y$축에 대칭이다.
3. $x<0$이면 $x$의 값이 증가할 때, $y$의 값은 감소한다.
   $x>0$이면 $x$의 값이 증가할 때, $y$의 값도 증가한다.
4. 원점을 제외한 모든 부분은 $x$축보다 위쪽에 있다.

함수 $y=-x^2$의 그래프는 함수 $y=x^2$의 그래프와 $x$축에 대칭이다.

이차함수 $y=ax^2$의 그래프

이제 $y=ax^2$의 그래프를 생각하자. 아래와 같이 $a\times x^2$으로 '$y$는 $x^2$과 정비례한다'고 생각하면 간단하게 이해할 수 있다. 예를 들면 함수 $y=x^2$의 그래프 위에 있는 모든 점을 $y$ 값을 두 배하여 옮기면 $y=2x^2$의 그래프가 된다.

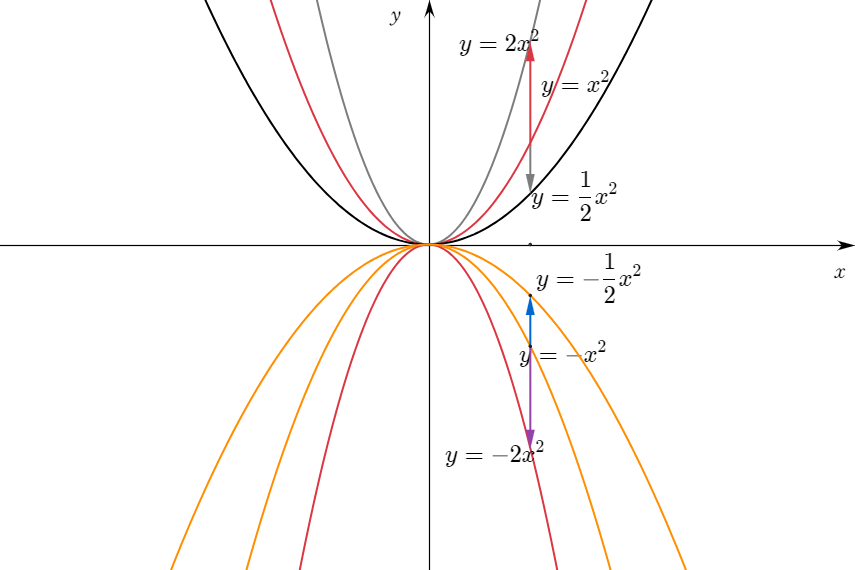
상수 $a$가 하는 일을 생각하면 쉽게 이해할 수 있다.

$a>0$이면 아래로 볼록하고 $a<0$이면 위로 볼록하다.

$|a|$가 클수록 그래프의 폭이 좁아지고 $y=ax^2$과 $y=-ax^2$은 서로 $x$축에 대칭이다.

이차함수 $y=ax^2$의 그래프와 같은 모양의 곡선을 포물선이라고 한다. 포물선은 선대칭도형이고, 대칭축을 포물선의 축이라고 하며, 포물선과 축과의 교점을 포물선의 꼭짓점이라고 한다.

이차함수 $y=x(5-x)$의 그래프

이제는 이차함수 $y=x(5-x)$도 쉽게 해석할 수 있다.

두 일차함수 $y=x$와 $y=5-x$의 그래프인 직선을 그리고 이차함수는 선대칭인 곡선 포물선이 된다는 사실을 생각하면 쉽게 이해할 수 있다.

먼저 $(0,0),\;\;(5,0)$을 지나는 위로 볼록한 포물선이다.

두 일차함수의 함숫값이 모두 양수일 때, 즉 $0<x<5$에서 $y>0$이므로 $x$축보다 위에 있다.

두 일차함수의 함숫값이 부호가 다를 때는 $x$축보다 아래에 있다.

축은 $\displaystyle{x=\frac{5}{2}}$이다. 꼭짓점은 $\displaystyle{\bigg(\frac{5}{2},\frac{25}{4}\bigg)}$